江西省宜春市第八中学2023-2024学年七年级下学期期中数学试题（原卷版+解析版）

这是一份江西省宜春市第八中学2023-2024学年七年级下学期期中数学试题（原卷版+解析版），文件包含江西省宜春市第八中学2023-2024学年七年级下学期期中数学试题原卷版docx、江西省宜春市第八中学2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
（满分100分，考试时间100分钟）
一、选择题（本大题共6小题，每小题3分，共18分）
1. 下列实数中，是无理数是（ ）
A 0B. C. D.
【答案】C
【解析】
【分析】本题考查了无理数的识别，无限不循环小数叫无理数，初中范围内常见的无理数有三类：①类，如，等；②开方开不尽的数，如，等；③虽有规律但却是无限不循环的小数，如（两个1之间依次增加1个0），（两个2之间依次增加1个1）等．
【详解】解：根据无理数定义可知，只有C选项中的数是无理数，
故选：C．
2. 如果，那么下列结论错误的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】根据不等式的性质，逐项判断即可求解．
【详解】解：A、如果，那么，故本选项正确，不符合题意；
B、如果，那么，故本选项正确，不符合题意；
C、如果，那么，故本选项正确，不符合题意；
D、如果，那么，故本选项错误，符合题意；
故选：D
【点睛】本题主要考查了不等式的性质，熟练掌握不等式两边加（或减）同一个数（或式子），不等号的方向不变；不等式两边乘（或除以）同一个正数，不等号的方向不变；不等式两边乘（或除以）同一个负数，不等号的方向改变．
3. 如图，这是一条马路上的人行横道线，即斑马线的示意图，请你根据图示判断，在过马路时三条线路AC，AB，AD中最短的是( )
A. ACB. ABC. ADD. 不确定
【答案】B
【解析】
【分析】根据在同一平面内垂线段最短求解．
【详解】解：根据在同一平面内垂线段最短，可知AB最短．
故选：B．
【点睛】本题主要考查了垂线段最短的性质．
4. 在数轴上表示不等式的解集，下列表示正确的是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】本题主要考查了解一元一次不等式，在数轴上表示不等式的解集，按照移项，系数化为1的步骤求出不等式的解集，在数轴上表示不等式的解集时向右画，向左画且“”，“”要用空心圆点表示，据此可得答案．
【详解】解：
移项得：，
系数化为1得：，
数轴表示如下：
故选：A．
5. 下列命题中，是真命题的是（ ）
A. 过直线外一点有且只有一条直线与已知直线平行
B. 同旁内角互补
C. 如果两个角的和为，那么这两个角是邻补角
D. 两点之间，直线最短
【答案】A
【解析】
【分析】本题主要考查了判断命题真假，平行线的性质与判断，邻补角的定义，两点之间，线段最短等等，熟练掌握相关知识是解题的关键．
【详解】解：A、过直线外一点有且只有一条直线与已知直线平行，原命题真命题，符合题意；
B、两直线平行，同旁内角互补，原命题是假命题，不符合题；
C、如果两个角的和为，那么这两个角是补角，不一定是邻补角，原命题是假命题，不符合题；
D、两点之间，线段最短，原命题是假命题，不符合题；
故选：A．
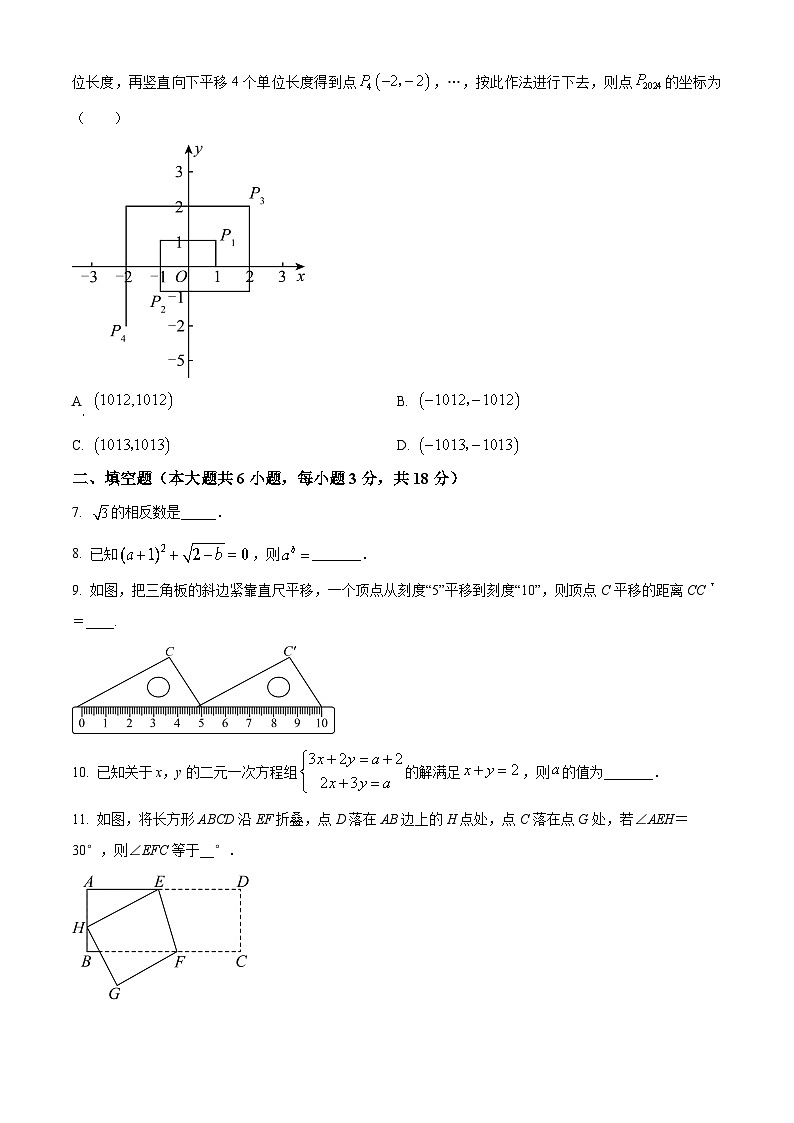
6. 如图，在平面直角坐标系中，动点P从原点O出发，水平向右平移1个单位长度，再竖直向上平移1个单位长度得点；接着水平向左平移2个单位长度，再竖直向下平移2个单位长度得到点；接着水平向右平移3个单位长度，再竖直向上平移3个单位长度得到点；接着水平向左平移4个单位长度，再竖直向下平移4个单位长度得到点，…，按此作法进行下去，则点的坐标为（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】本题主要考查了点的坐标规律探索，观察可知，偶数点都在第三象限，且可以得到规律，据此可得答案．
【详解】解：，
，
，
……，
以此类推可知，，
∵，
∴点的坐标为，
故选：B．
二、填空题（本大题共6小题，每小题3分，共18分）
7. 的相反数是_____．
【答案】
【解析】
【详解】只有符号不同的两个数互为相反数，
由此可得的相反数是-，
故答案为：-.
8. 已知，则_______．
【答案】
【解析】
【分析】本题考查的是非负数的性质，先根据非负数的性质求出的值，再进行计算即可，熟知当几个数或式的偶次方相加和为时，则其中的每一项都必须等于是解题的关键．
【详解】解：∵，
∴，
∴，
∴，
故答案为：．
9. 如图，把三角板的斜边紧靠直尺平移，一个顶点从刻度“5”平移到刻度“10”，则顶点C平移的距离CC＇＝____.

【答案】5
【解析】
【详解】解：∵把三角板的斜边紧靠直尺平移，一个顶点从刻度“5”平移到刻度“10”，∴三角板向右平移了5个单位，
∴顶点C平移的距离CC′=5．
故答案为5．
【点睛】本题考查平移的性质，简单题目．
10. 已知关于x，y的二元一次方程组的解满足，则的值为_______．
【答案】
【解析】
【分析】本题主要考查了二元一次方程组的解，把二元一次方程组的两个方程相加即可得到，结合题干条件即可求出的值，解题的关键是能观察出方程组未知数系数的关系．
【详解】解：，
，得：，
∵，
∴，
解得：，
故答案为：．
11. 如图，将长方形ABCD沿EF折叠，点D落在AB边上的H点处，点C落在点G处，若∠AEH＝30°，则∠EFC等于__°．

【答案】105
【解析】
【分析】根据折叠得出∠DEF＝∠HEF，求出∠DEF的度数，根据平行线的性质得出∠DEF+∠EFC＝180°，代入求出即可．
【详解】解：∵将长方形ABCD沿EF折叠，点D落在AB边上的H点处，点C落在点G处，
∴∠DEF＝∠HEF，
∵∠AEH＝30°，
∴∠DEF＝∠HEF＝（180°﹣∠AEH）＝75°，
∵四边形ABCD是长方形，
∴AD∥BC，
∴∠DEF+∠EFC＝180°，
∴∠EFC＝180°﹣75°＝105°，
故答案为：105．
【点睛】本题主要考查了折叠的性质和平行线的性质应用，准确计算是解题的关键．
12. 如图所示，在长方形中，点O是平面直角坐标系原点，B点坐标为，有一动点P从原点出发，以每秒1个单位长度的速度沿着的路线移动，到A点停止运动．在点P移动的过程中，当三角形的面积是8时，则P点运动的时间为_______秒．
【答案】4或或14
【解析】
【分析】本题主要考查了坐标与图形，先求出，再分当点P在上时，当点P在上时，当点P在上时，三种情况根据三角形面积公式列出方程求出点P的运动路程，进而求出运动时间即可．
【详解】解：∵在长方形中，点O是平面直角坐标系的原点，B点坐标为，
∴，
当点P在上时，
∵三角形的面积是8，
∴，即，
∴，
∴此时运动时间为4秒；
当点P在上时，
∵三角形的面积是8，
∴，即，
∴，
∴此时运动时间为秒；
当点P在上时，
∵三角形的面积是8，
∴，即，
∴，
∴此时运动时间为秒；
综上所述，P点运动的时间为4秒或秒或14秒，
故答案为：4或或14．
三、解答题（本大题共5题，每小题6分，共30分）
13. （1）计算：；
（2）解方程：．
【答案】（1）；（2）．
【解析】
【分析】本题考查了解二元一次方程组，实数的运算，熟练掌握方程组的解法及运算法则是解题的关键．
（1）利用算术平方根，立方根的定义，以及二次根式性质计算即可；
（2）利用加减消元法求解即可．
【详解】解：（1）
；
（2）
，得：，
解得：，
把代入得：，
∴方程组的解是：．
14. 已知一个正数x两个平方根分别为和，的立方根是．
（1）求a，b的值；
（2）求的立方根．
【答案】（1），
（2）
【解析】
【分析】本题主要考查了平方根和立方根的概率，代数式求值：
（1）根据一个正数的两个平方根互为相反数得到，解方程可求出a；根据立方根的定义可得，解方程即可求出b；
（2）根据（1）所求结合平方根的概念求出x的值，然后代值计算即可．
【小问1详解】
解：∵一个正数x的两个平方根分别为和，
∴，
∴；
∵的立方根是
∴，
∴；
【小问2详解】
解：由（1）得，
∴，
∴，
∴的立方根为3．
15. 如图，在平面直角坐标系中，三角形三个顶点的坐标分别是，，，三角形中任意一点，经平移后对应点为，三角形作同样的平移得到三角形，点A，B，C对应点分别为．
（1）画出平移后的三角形；
（2）求三角形的面积．
【答案】（1）见解析 （2）
【解析】
【分析】本题主要考查了坐标与图形变化—平移，网格中求三角形面积：
（1）先根据、可得平移方式为向左平移了8个单位，向上平移了2个单位，据此求出的坐标，再描出，最后顺次连接即可；
（2）用三角形所在的长方形面积减去周围三个三角形面积即可得到答案．
【小问1详解】
解：由到可知平移方式为向左平移了8个单位，向上平移了2个单位，
∴，，
即，，，
如下图所示，三角形即为所求；
【小问2详解】
解：．
16. 已知平面直角坐标系中有一点．
（1）若点M在y轴上，求点M的坐标；
（2）若点M位于第二象限，且到x轴的距离为1，求点M的坐标．
【答案】（1）的坐标为
（2）点的坐标为
【解析】
【分析】本题考查了点坐标，熟练掌握平面直角坐标系中，点坐标的特征是解题关键．
（1）根据轴上的点的横坐标为可求出的值，由此即可得；
（2）根据“点到轴的距离为”可得， 求出的值，由此即可得．
【小问1详解】
解：∵点在轴上，
∴，
解得，
∴，
∴的坐标为．
【小问2详解】
解：∵点到轴的距离为，
∴，
解得或，
当时， ，，
当时，，，
∵点M位于第二象限，
∴点的坐标为．
17. 如图，直线与相交于点O，．
（1）若，证明：；
（2）若，求的度数．
【答案】（1）证明见解析；
（2）．
【解析】
【分析】本题考查了垂直的定义，证明两条直线垂直，只需要证明这两条直线相交所成的四个角中有一个角是直角．
（1）根据垂直的定义可得，进一步得到即可求证；
（2）由，得到，求出，即可求解．
【小问1详解】
解：∵，
∴，
∴，
∵，
∴，
即，
∴．
【小问2详解】
解：∵，
∴，
解得：，
∴．
四、解答题（本大题共3题，每小题8分，共24分）
18. 如图，已知，，平分，．
（1）证明：；
（2）若，求的度数．
【答案】（1）证明见解析；
（2）．
【解析】
【分析】本题考查了平行线的判定与性质，角平分线的性质，掌握平行线的判定与性质是解题的关键．
（1）由，得到，再由，得到，即可求证；
（2）由平行线的性质得到，再由，求出，根据角平分线的性质即可求解．
【小问1详解】
证明：∵，
∴，
∵，
∴，
∴．
【小问2详解】
解：∵，
∴，
∵，
∴，
∵，
∴，
∴，
∴，
∴，
∵平分，
∴．
19. 我国传统数学名著《九章算术》记载：“今有牛五、羊二，直金十九两；牛二、羊五，直金十六两．问牛、羊各直金几何？”译文：“假设有5头牛、2只羊，值19两银子；2头牛、5只羊，值16两银子，问每头牛、每只羊分别值银子多少两？”
根据以上译文，提出以下两个问题：
（1）求每头牛、每只羊各值多少两银子？
（2）若某商人准备用19两银子买牛和羊（要求既有牛也有羊，且银两须全部用完），请问商人有几种购买方法？列出所有的可能．
【答案】(1) 每头牛3两银子,每只羊2两银子;(2) 三种购买方法, 买牛5头,买养2只或买牛3头,买养5只或买牛1头,买养8只．
【解析】
【分析】(1)根据题意列出二元一次方程组,解出即可．
(2)根据题意列出代数式,穷举法代入取值即可．
【详解】(1)设每头牛x银两,每只羊y银两．
解得:
答:每头牛3两银子,每只羊2两银子．
(2)设买牛a头,买羊b只．
3a+2b=19,即．
解得a=5,b=2；或a=3,b=5,或a=1,b=8．
答:三种购买方法, 买牛5头,买养2只或买牛3头,买养5只或买牛1头,买羊8只．
【点睛】本题考查二元一次方程组的应用,关键在于理解题意找出等量关系．
20. 先阅读下列一段文字，再解答问题
已知在平面内有两点，其两点间的距离公式为，同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为或．
（1）已知点，则 ；
（2）已知点C、D在平行于y轴的直线上，点C的纵坐标为6，点D的纵坐标为，则 ；
（3）已知点，并且，求m的值．
【答案】（1）；
（2）；
（3）m的值为或．
【解析】
【分析】此题主要考查两点间距离公式，读懂题意，根据题意给出的形式或公式进行套用进行作答即可．
（1）根据题意即可作答；
（2）由平行于轴，根据题意公式计算即可；
（3）利用两点间距离公式分别求出、，即可求解．
【小问1详解】
解：∵，
∴
故答案为：．
【小问2详解】
解：∵点C、D在平行于y轴的直线上，点C的纵坐标为6，点D的纵坐标为，
∴，
故答案为：．
【小问3详解】
解：∵，
∴，
∵点与点的纵坐标相等，
∴点、两点所在的直线平行于 轴，
∴，
∵，
∴，
解得：或，
∴m的值为或．
五、解答题（本大题共1题，共10分）
21. 如图1，，点A、C分别在射线和上，．
（1）若，则 ；
（2）小明同学发现：无论如何变化，的值始终为定值，并给出了一种证明该发现的辅助线作法：如图2，过作A作，交于M．请你根据小明同学提供的轴助线（或自己添加其它辅助线），确定该定值，并说明理由；
（3）如图3，若把题干中的“改为“”，其它条件保持不变，试猜想与的数量关系，并说明理由．
【答案】（1）
（2），理由见解析
（3）．理由解解析
【解析】
【分析】本题主要考查了平行线的性质与判定：
（1）过点F作，如图，由已知，，根据平行线的性质可计算出的度数，由，可计算出的度数，由平行线的性质即可得出答案；
（2）由已知条件，根据平行线的性质可得，计算出的度数，由平行线的性质可得，由即可得出答案；
（3）过点A作与相交与点N，再同（2）求解即可．
【小问1详解】
解：过点F作，如图所示，
∵，
∴，
∴，
∵，
∴，
∵，
∴，
∴．
故答案为：；
【小问2详解】
解：该定值为．理由如下：
∵，，
∴，．
∵，
∴．
∴．
∴．
∴无论如何变化，的值始终为定值，且该定值为．
【小问3详解】
解：．理由如下：
过点A作，交于点N，如图所示，
∵，，
∴，．
∵，
∴．
∴．
∴．