






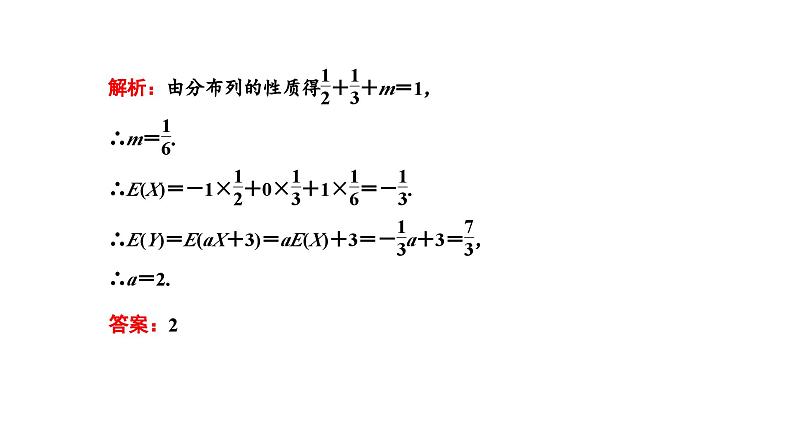
所属成套资源:全套人教A版高中数学选择性必修第三册课时教学课件
人教A版 (2019)选择性必修 第三册7.3 离散型随机变量的数字特征教学演示ppt课件
展开
这是一份人教A版 (2019)选择性必修 第三册7.3 离散型随机变量的数字特征教学演示ppt课件,共32页。
题型三 离散型随机变量均值的实际应用 [学透用活] [典例3] 现有甲、乙两个投资项目,对甲项目投资10万元,根据对市场120份样本数据的统计,甲项目年利润分布如表:
记随机变量X,Y分别表示对甲、乙两个项目各投资10万元的年利润.将甲项目年利润的频率作为对应事件的概率.(1)求X>Y的概率;(2)某商人打算对甲或乙项目投资10万元,判断哪个项目更具有投资价值,并说明理由.
[方法技巧]1.实际问题中的均值问题均值在实际中有着广泛的应用,如在体育比赛的安排和成绩预测、消费预测、工程方案的预测、产品合格率的预测、投资收益等,都可以通过随机变量的均值来进行估计.2.概率模型的解答步骤(1)审题,确定实际问题是哪一种概率模型,可能用到的事件类型,所用的公式有哪些.(2)确定随机变量的分布列,计算随机变量的均值.(3)对照实际意义,回答概率、均值等所表示的结论.
[对点练清]某中药种植基地有两处种植区的药材需在下周一、下周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘.由于下雨会影响药材品质,基地收益如表所示:
若基地额外聘请工人,可在周一当天完成全部采摘任务.无雨时收益为20万元;有雨时收益为10万元.额外聘请工人的成本为a万元.已知下周一和下周二有雨的概率相同,两天是否下雨互不影响,基地收益为20万元的概率为0.36.(1)若不额外聘请工人,写出基地收益X的分布列及基地的预期收益;(2)该基地是否应该额外聘请工人,请说明理由.
解:(1)设下周一无雨的概率为p,由题意知,p2=0.36,p=0.6,基地收益X的可能取值为20,15,10,7.5,则P(X=20)=0.36,P(X=15)=0.24,P(X=10)=0.24,P(X=7.5)=0.16,所以基地收益X的分布列为
基地的预期收益E(X)=20×0.36+15×0.24+10×0.24+7.5×0.16=14.4(万元),所以基地的预期收益为14.4万元.
(2)设基地额外聘请工人时的收益为Y万元,则其预期收益E(Y)=20×0.6+10×0.4-a=16-a(万元),E(Y)-E(X)=1.6-a.综上,当额外聘请工人的成本高于1.6万元时,不额外聘请工人;成本低于1.6万元时,额外聘请工人;成本恰为1.6万元时,是否额外聘请工人均可以.
相关课件
这是一份高中数学人教A版 (2019)选择性必修 第三册7.3 离散型随机变量的数字特征教学课件ppt,共40页。PPT课件主要包含了自学导引,加权平均数,平均水平,两点分布的期望,aEX+b,课堂互动,答案A,素养达成,答案D等内容,欢迎下载使用。
这是一份人教A版 (2019)选择性必修 第三册7.3 离散型随机变量的数字特征教学课件ppt,共26页。
这是一份高中数学人教A版 (2019)选择性必修 第三册7.3 离散型随机变量的数字特征优质课件ppt,共5页。PPT课件主要包含了复习回顾,新课引入,新知探究,概念生成,典例解析,方法归纳,巩固练习,课堂小结等内容,欢迎下载使用。










