高中数学人教A版 (2019)必修 第一册1.3 集合的基本运算授课ppt课件

这是一份高中数学人教A版 (2019)必修 第一册1.3 集合的基本运算授课ppt课件，共26页。PPT课件主要包含了学习目标，知识点一全集，所有元素，全集一定是实数集吗，提示不一定，知识点二补集，x｜x≤1，答案1C，答案2C，1U＝R等内容，欢迎下载使用。

某学习小组学生的集合为U＝{王明,曹勇,王亮,李冰,张军,赵云,冯佳,薛香芹,钱忠良,何晓慧},其中在学校应用文写作比赛与技能大赛中获得过金奖的学生集合为P＝{王明,曹勇,王亮,李冰,张军}.
问题　没有获得金奖的学生有哪些?
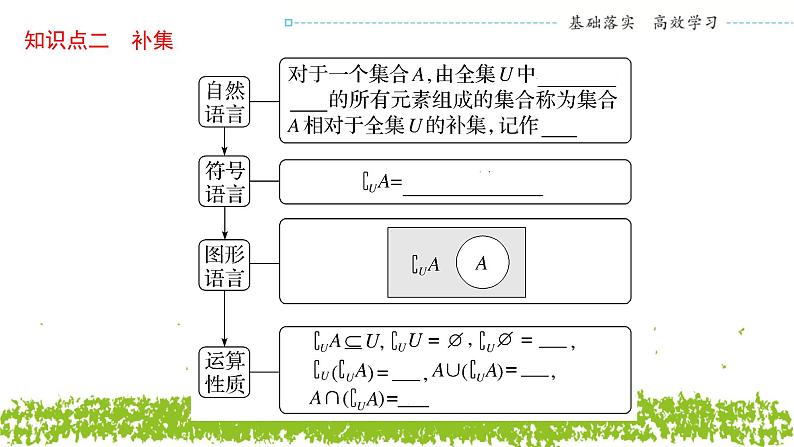
1.概念:如果一个集合含有所研究问题中涉及的 　所有元素　⁠,那么就称这个集合为全集.
2.记法:通常记作 　U　⁠.
提醒　(1)补集是相对于全集而言的,它与全集不可分割;(2)补集既是集合之间的一种关系,同时也是集合之间的一种运算.求集合A的补集的前提是A为全集U的子集,随着所选全集的不同,得到的补集也是不同的.
1.设全集U＝{0,1,2,3,4,5},A＝{2,4},则∁UA＝(　　)
解析:D　因为全集U＝{0,1,2,3,4,5},A＝{2,4},所以∁UA＝{0,1,3,5}.
2.已知全集U＝{0,1,2},且∁UA＝{2},则A＝ 　　　　⁠. 
解析:∵U＝{0,1,2},∁UA＝{2},∴A＝{0,1}.
3.若集合A＝{x｜x＞1},则∁RA＝ 　　　　⁠. 
解析:∵A＝{x｜x＞1},∴∁RA＝{x｜x≤1}.
【例1】　(1)设全集U＝{1,2,3,4,5,6},M＝{1,2,4},则∁UM＝(　　)
解析　(1)因为U＝{1,2,3,4,5,6},M＝{1,2,4},由补集的定义,可知∁UM＝{3,5,6}.
(2)若全集U＝{x∈R｜-2≤x≤2},集合A＝{x∈R｜-2≤x≤0},则∁UA＝(　　)
解析　(2)借助数轴(如图)易得∁UA＝{x∈R｜0＜x≤2}.
通性通法求集合补集的2种方法(1)当集合用列举法表示时,直接用定义或借助Venn图求解;(2)当集合是用描述法表示的连续数集时,可借助数轴,利用数轴分析求解.
　若集合A＝{x｜-1≤x＜1},当U分别取下列集合时,求∁UA.
解:(1)把集合U和A表示在数轴上,如图①所示.
由图知∁UA＝{x｜x＜-1或x≥1}.
(2)U＝{x｜x≤2};
解:(2)把集合U和A表示在数轴上,如图②所示.
由图知∁UA＝{x｜x＜-1或1≤x≤2}.
(3)U＝{x｜-4≤x≤1}.
解:(3)把集合U和A表示在数轴上,如图③所示.
由图知∁UA＝{x｜-4≤x＜-1或x＝1}.
【例2】　(1)(2022·全国甲卷)设全集U＝{-2,-1,0,1,2,3},集合A＝{-1,2},B＝{x｜x2-4x＋3＝0},则∁U(A∪B)＝(　　)
解析　(1)集合B＝{1,3},所以A∪B＝{-1,1,2,3},所以∁U(A∪B)＝{-2,0}.故选D.
(2)设全集为R,A＝{x｜3≤x＜7},B＝{x｜2＜x＜10},则∁R(A∪B)＝ 　　　　⁠,(∁RA)∩B＝ 　　　　⁠. 
解析　(2)把全集R和集合A,B在数轴上表示如图,由图知,A∪B＝{x｜2＜x＜10},所以∁R(A∪B)＝{x｜x≤2,或x≥10}.因为∁RA＝{x｜x＜3,或x≥7},所以(∁RA)∩B＝{x｜2＜x＜3,或7≤x＜10}.
答案　(2){x｜x≤2,或x≥10}　{x｜2＜x＜3,或 7≤x＜10}
通性通法解决集合交、并、补综合运算的技巧(1)如果所给集合是有限集,则先把集合中的元素一一列举出来,然后结合交集、并集、补集的定义来求解.在解答过程中常常借助于Venn图来求解;(2)如果所给集合是无限实数集,则常借助数轴,把已知集合及全集分别表示在数轴上,然后进行交、并、补集的运算.提醒　解答过程中要注意边界.
解:将集合A,B,P分别表示在数轴上,如图所示.
因为U＝R,A＝{x｜-4≤x＜2},B＝{x｜-1＜x≤3},
所以A∩B＝{x｜-1＜x＜2},∁UB＝{x｜x≤-1或x＞3}.
所以(A∩B)∩(∁UP)
＝{x｜0＜x＜2}.
【例3】设集合A＝{x｜x＋m≥0},B＝{x｜-2＜x＜4},全集U＝R,且(∁UA)∩B＝⌀,求实数m的取值范围.
由已知A＝{x｜x≥-m},
得∁UA＝{x｜x＜-m},
因为B＝{x｜-2＜x＜4},(∁UA)∩B＝⌀,在数轴上画出∁UA与B,如图,
所以-m≤-2,即m≥2,
所以实数m的取值范围是{m｜m≥2}.
(变条件)本例将条件“(∁UA)∩B＝⌀”改为“(∁UB)∪A＝R”,其他条件不变,则实数m的取值范围又是什么?
解:由已知A＝{x｜x≥-m},∁UB＝{x｜x≤-2或x≥4}.又(∁UB)∪A＝R,所以-m≤-2,即m≥2.故实数m的取值范围为{m｜m≥2}.
通性通法由集合的补集求参数的方法(1)如果所给集合是有限集,由补集求参数问题时,可利用补集定义求解;(2)如果所给集合是无限集,与集合交、并、补运算有关的求参数问题时,一般利用数轴分析求解.
1.已知全集U＝{3,4,a2＋2a＋3},集合A＝{3,4},∁UA＝{6},则实数a的值为 　　　　⁠. 
解析:由题意得a2＋2a＋3＝6,解得a＝-3或a＝1,经检验均符合题意.
2.已知全集U＝R,A＝{x｜1≤x＜b},∁UA＝{x｜x＜1,或x≥2},则实数b＝ 　　　　⁠. 
解析:因为∁UA＝{x｜x＜1,或x≥2},所以A＝{x｜1≤x＜2}.所以b＝2.
1.若全集U＝{1,2,3,4},集合M＝{1,2},N＝{2,3},则∁U(M∪N)＝(　　)
解析:D　∵全集U＝{1,2,3,4},集合M＝{1,2},N＝{2,3},∴M∪N＝{1,2,3},∴∁U(M∪N)＝{4}.故选D.
2.(2022·全国乙卷)设全集U＝{1,2,3,4,5},集合M满足∁UM＝{1,3},则(　　)
解析:A　由题意知M＝{2,4,5},故选A.
3.已知全集U＝R,集合A＝{x｜x≤5},B＝{x｜x＞0},则集合∁U(A∩B)＝(　　)
解析:D　由已知A∩B＝{x｜0＜x≤5},故∁U(A∩B)＝{x｜x≤0或x＞5}.
4.已知全集U＝{x｜x≤4},集合A＝{x｜-2＜x＜3},B＝{x｜-3≤x≤2},求A∩B,(∁UA)∪B,A∩(∁UB).
解:如图,在数轴上表示集合A,B,U.
∵A＝{x｜-2＜x＜3},B＝{x｜-3≤x≤2},U＝{x｜x≤4},
∴A∩B＝{x｜-2＜x≤2},∁UA＝{x｜x≤-2,或3≤x≤4},∁UB＝{x｜x＜-3,或2＜x≤4}.
∴(∁UA)∪B＝{x｜x≤2,或3≤x≤4},A∩(∁UB)＝{x｜2＜x＜3}.