中考数学一轮教材梳理复习课件 第15课时　等腰三角形

这是一份中考数学一轮教材梳理复习课件 第15课时　等腰三角形，共29页。PPT课件主要包含了平分线，或11，°或75°等内容，欢迎下载使用。
1. 等腰三角形有一个角是90°，则另两个角的度数分别是( )A. 30°，60°B. 45°，45°C. 45°，90°D. 20°，70°2. 若一个等腰三角形的两边长分别为2，4，则第三边的长为( )A. 2 B. 3 C. 4 D. 2或4
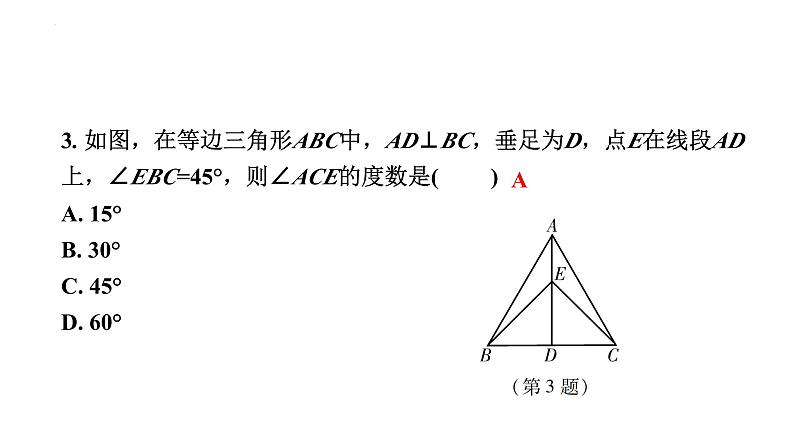
3. 如图，在等边三角形ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC=45°，则∠ACE的度数是( )A. 15°B. 30°C. 45°D. 60°
考点1等腰三角形的判定和性质
EXAM KEY POINTS
1. 等腰三角形的判定. (1)①有两个角相等的三角形是等腰三角形；②有两条边相等的三角形是等腰三角形. (2)若一个三角形中有两个角相等，则这两个角所对的边也相等(即“等角对等边”).
2. 等腰三角形的性质. (1)等腰三角形的两条腰　 　.   (2)等腰三角形的两个底角　 　(简写为“等边对等角”).   (3)等腰三角形的顶角　 　，底边上的　 　，底边上的　 　互相重合(即“三线合一”).  (4)等腰三角形是轴对称图形，至少有一条对称轴.
【例 1】如图，在Rt△ABC中，∠C=90°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为( )A. 4个B. 5个C. 6个D. 7个
技巧引导：本题考查了等腰三角形的判定的应用，主要考查学生的理解能力和动手操作能力，如图.
考点2等边三角形的性质及判定
3. 等边三角形的性质. (1)等边三角形的三条边　 　.  (2)等边三角形的每个角都等于　 　.  (3)等边三角形是轴对称图形，并且有　 　条对称轴.  温馨提示：等边三角形是特殊的等腰三角形，所以它具有等腰三角形的所有性质.
4. 等边三角形的判定. (1)三条边都相等的三角形是等边三角形. 三个角都相等的三角形是等边三角形. (2)有两个角等于60°的三角形是等边三角形. (3)有一个角等于60°的等腰三角形是等边三角形.
【例 2】(2023·三明模拟)如图，在△ABC中，∠ABC=60°，将△ABC的边AC平移到BD处(点B为点C的对应点)，再将△ABC 绕点B逆时针旋转60°至△A'BC'，延长C'A'交BD于点E，连接C'D.
(1)连接AA'，求证：AA'=AB. (2)求证：A，A'，D三点共线.
证明：(1)∵△ABC绕点B逆时针旋转60°至△A'BC'，∴∠A'BA=∠C'BC=60°，BA'=BA. ∴△BAA'是等边三角形. ∴AA'=AB.
(2)连接AD. ∵线段CA平移得到线段BD(其中点B和点C对应)，∴CA∥BD，CA=BD. ∴四边形ACBD是平行四边形. ∴AD∥BC. ∴∠BAD=∠ABC=60°. 由(1)知△BAA'是等边三角形，∴∠BAA'=60°. ∴∠BAA'=∠BAD. ∴ A，A'，D三点共线.
考点3线段的垂直平分线
5. 性质：线段垂直平分线上的点与这条线段两个端点的距离　 　.  6. 判定：与线段两个端点距离　 　的点在这条线段的垂直平分线上.  温馨提示：线段的垂直平分线可以看作是到线段两个端点距离相等的所有点的集合.
【例 3】如图，在△ABC中，AB的垂直平分线DE交AB于点D，交BC于点E，连接AE. 若BC=6，AC=5，则△ACE的周长为( )A. 8 B. 11C. 16 D. 17技巧引导：根据线段的垂直平分线的性质得到EB=EA，再根据三角形的周长公式计算即可.
A基础达标1. 如图，在△ABC中，AB=AC，∠A=40°，CD∥AB，则∠BCD的度数是( )A. 40° B. 50°C. 60° D. 70°
2. 如图，在△ABC中，∠C=90°，DE垂直平分AB，分别交AB，BC于D，E两点，若BE=5，CE=3，则AC的长为( )A. 5　B. 4C. 3　　D. 2
3. 如图，△ABC是等边三角形，l1∥l2，若∠α=25°，则∠β等于( )A. 35° B. 30°C. 25° D. 20°
5. (2023·福州期中)如图，等边三角形ABC的三个顶点都在坐标轴上，A(－1，0)，过点B作BD⊥AB，垂线BD交x轴于点D，则点D的坐标为　 　.  
6. (2023·宁德期末)如图，已知△ABC，AB=AC，E是线段AB上的一个动点，CE的垂直平分线交AC于点M，交CE于点O，交BC于点N. (1)当∠A=80°，∠BCE=20°时，求∠ACE的度数. (2)当CE平分∠ACB时，求证：△EOM≌△CON.
(1)解：∵ AB=AC，∴∠B=∠BCE＋∠ACE. ∵∠A=80°，∴∠B=∠BCE＋∠ACE=50°. ∵∠BCE=20°，∴∠ACE=30°.
B能力创优7. 如图，在4×4的正方形网格中有两个格点A，B，连接AB，在网格中再找一个格点C，使得△ABC是等腰直角三角形，满足条件的格点C的个数是( )A. 2 B. 3 C. 4 D. 5
8. (改编题)如图，在△ABC中，AB=AC，∠B=70°. 若以点C为圆心，CA长为半径作弧，交直线BC于点P，连接AP，则∠BAP的度数是　 .