中考数学一轮复习 课件 第23讲　相似三角形

这是一份中考数学一轮复习 课件 第23讲　相似三角形，共26页。PPT课件主要包含了思维导图，夯实基础，考点2黄金分割，相似比，相似比为1，点对点练习，第4题，对应角相等，相似比的平方，第5题等内容，欢迎下载使用。
考点1成比例线段和平行线分线段成比例
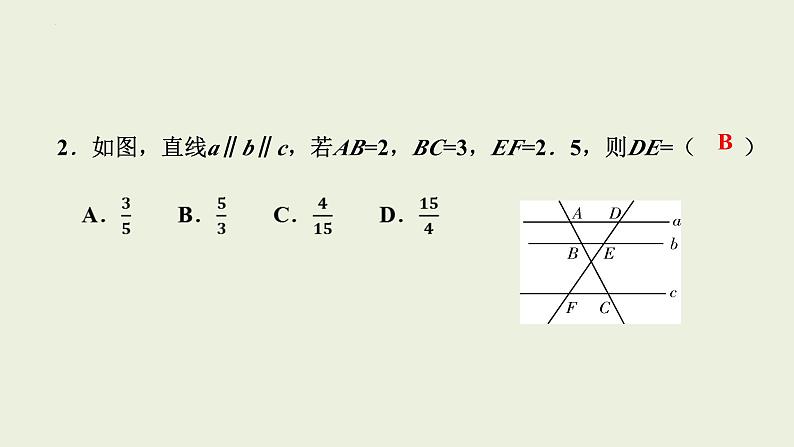
2．如图，直线a∥b∥c，若AB=2，BC=3，EF=2．5，则DE=（ ）
点对点练习　　　　　 　　　　 　　　　 3．（2022·山西）神奇的自然界处处蕴含着数学知识．动物学家在鹦鹉螺外壳上发现，其每圈螺纹的直径与相邻螺纹直径的比约为0.618．这体现了数学中的（ ）A．平移B．旋转C．轴对称D．黄金分割
知识梳理1．相似三角形的定义三个角分别相等，三条边成比例的两个三角形叫做相似三角形．相似三角形对应边的比叫做__________，通常用字母k表示．全等三角形是______________的特殊的相似三角形． 2．相似三角形的判定方法（1）平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似；（2）三边对应成比例，两个三角形相似；（3）两边对应成比例且夹角相等，两个三角形相似；（4）两角分别相等，两个三角形相似．
考点3相似三角形的定义和判定
4．如图，△ABC中，∠A=76°，AB=8，AC=6．将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（ ）
知识梳理1．相似三角形的__________________，对应边成比例． 2．相似三角形的对应高的比、对应中线的比、对应角平分线的比都等于____________． 3．相似三角形的周长比等于相似比．4．相似三角形的面积比等于___________________． 
考点4相似三角形的性质
点对点练习　　　　　 　　　　 　　　　 5．如图，在矩形ABCD中，点E，F分别在边AD，DC上，△ABE∽△DEF，AB=6，DE=2，DF=3，则BE的长是_________． 
知识梳理1．定义：如果两个图形不仅是相似图形，而且每组对应点的连线都经过同一个点，那么这样的两个图形叫做位似图形，这个点叫做位似中心，此时的相似比叫做位似比．2．性质：①每一组对应点和位似中心在同一直线上，它们到位似中心的距离之比都等于___________；②位似图形的面积比等于_________________． 3．在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或－k．4．已知图形的位似图形有两个，在位似中心的两侧各有一个．
点对点练习　　　　　 　　　　 　　　　 6．如图，△ABC与△DEF位似，点O是它们的位似中心，且位似比为1∶2，则△ABC与△DEF的周长之比是（ ）A．1∶2
B．1∶4C．1∶3D．1∶9
7．如图，以点O为位似中心，将△ABC放大为原来的2倍．
解：如图，△A'B'C'即为所求．
【例】（2023·广东）边长分别为10，6，4的三个正方形拼接在一起，它们的底边在同一直线上（如图），则图中阴影部分的面积为　__________． 
【变式】把边长分别为1和2的两个正方形按如图所示的方式放置，则图中阴影部分的面积是______． 
3．如图，在边长为1的小正方形组成的网格中，A，B，C，D四个点均在格点上，AC与BD相交于点E，连接AB，CD，AB∥CD，则△ABE与△CDE的周长比为（ ）A．1∶4 B．4∶1C．1∶2 D．2∶1
7．如图，点D和点E分别在AB，AC边上，BE平分∠ABC，BE，CD相交于点F，∠ABE=∠ACD．求证：（1）EC2=EF·EB；（2）DF ∶BF=EC ∶BC．