




中考数学一轮复习 课件 第26课 平行四边形
展开
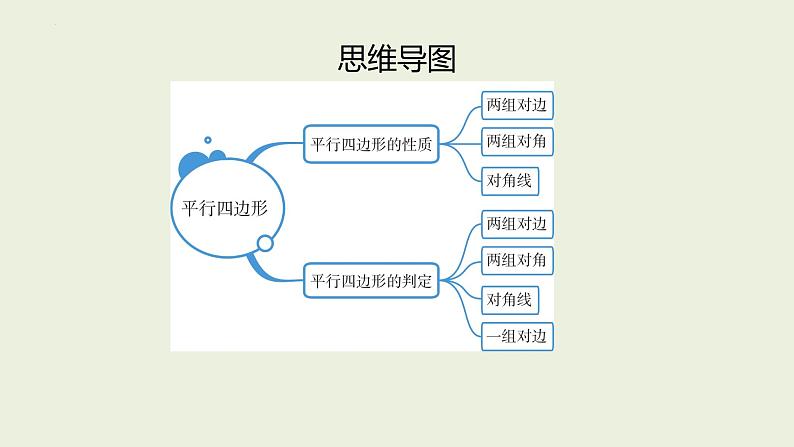
这是一份中考数学一轮复习 课件 第26课 平行四边形,共23页。PPT课件主要包含了思维导图,两组对边分别平行,对边相等,对角相等,对角线互相平分,夯实基础,第2题,115°,两组对边,对角线等内容,欢迎下载使用。
知识梳理1.平行四边形的定义:______________________的四边形叫做平行四边形. 2.平行四边形的性质:(1)平行四边形的___________________; (2)平行四边形的___________________; (3)平行四边形的____________________. 3.平行四边形的周长:C=2(a+b).
考点1平行四边形的性质
4.平行四边形的面积:(1)平行线之间的距离处处相等;(2)S=ah.5.平行四边形是中心对称图形.
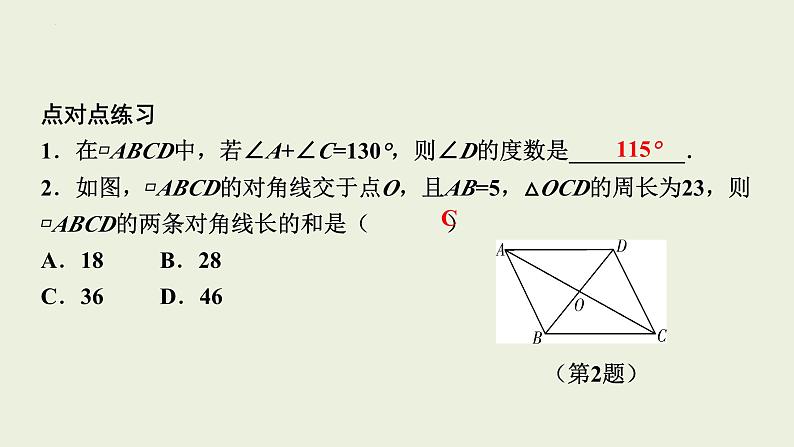
点对点练习 1.在▱ABCD中,若∠A+∠C=130°,则∠D的度数是__________. 2.如图,▱ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则▱ABCD的两条对角线长的和是( )A.18B.28C.36D.46
知识梳理1._____________分别平行的四边形是平行四边形. 2.两组对边分别_____________的四边形是平行四边形. 3.一组对边____________且__________的四边形是平行四边形. 4._____________互相平分的四边形是平行四边形.
考点2平行四边形的判定
点对点练习 3.在四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是( )A.OA=OC,OB=ODB.AD∥BC,AB∥DCC.AB=DC,AD=BCD.AB∥DC,AD=BC
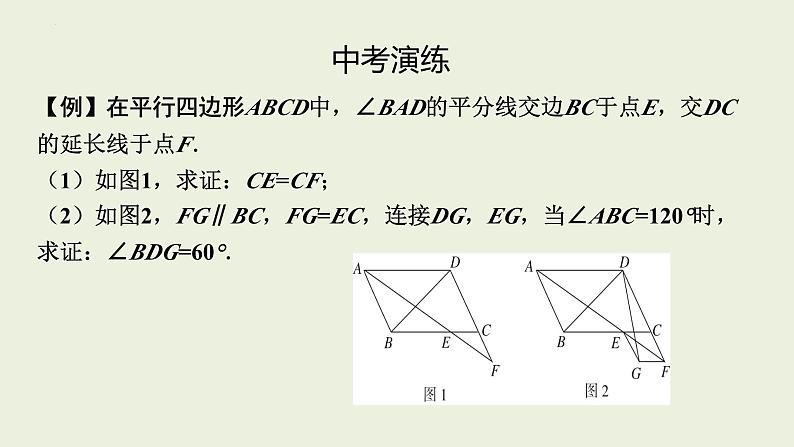
【例】在平行四边形ABCD中,∠BAD的平分线交边BC于点E,交DC的延长线于点F.(1)如图1,求证:CE=CF;(2)如图2,FG∥BC,FG=EC,连接DG,EG,当∠ABC=120°时,求证:∠BDG=60°.
证明:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC.∴∠F=∠BAF,∠CEF=∠DAF.∵AF平分∠BAD,∴∠BAF=∠DAF.∴∠F=∠CEF.∴CE=CF.(2)延长AB,FG交于点H,连接DH.∵FG∥CE,CE∥AD,∴FH∥BC∥AD.∵AH∥DF,∴四边形AHFD是平行四边形.∵∠DFA=∠FAB=∠DAF,∴DA=DF.∴四边形AHFD是菱形.∴FD=FH=AD=AH.
【变式】如图,在▱ABCD中,E为CD边的中点,连接BE并延长,交AD的延长线于点F,延长ED至点G,使DG=DE,分别连接AE,AG,FG.(1)求证:△BCE≌△FDE.(2)当BF平分∠ABC时,四边形AEFG是什么特殊四边形?请说明理由.
(2)解:四边形AEFG是矩形.理由如下:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC.∴∠AFB=∠FBC.由(1),得△BCE≌△FDE,∴BC=FD,BE=FE.∴FD=AD.∵GD=DE,∴四边形AEFG是平行四边形.∵BF平分∠ABC,∴∠FBC=∠ABF.∴∠AFB=∠ABF.∴AF=AB.∵BE=FE,∴AE⊥FE.∴∠AEF=90°.∴平行四边形AEFG是矩形.
A组基础1.如图,在▱ABCD中,一定正确的是 ( )A.AD=CD B.AC=BDC.AB=CD D.CD=BC
2.如图,四边形ABCD为平行四边形,则点B的坐标为 .
3.如图,点E,F分别在▱ABCD的边AB,CD的延长线上,连接EF,分别交AD,BC于点G,H.添加一个条件使△AEG≌△CFH,这个条件可以是 .(只需写一种情况)
4.如图,将平行四边形ABCD的对角线AC向两个方向延长,分别至点E和点F,且使得AE=CF,求证:四边形EBFD为平行四边形.
证明:连接BD,与AC交于点O.∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.又∵AE=CF,∴OA+AE=OC+CF,即OE=OF.∴四边形EBFD是平行四边形.
B组提升5.(2023·广东汕头一模)如图,△ABC为等边三角形,D为BC的中点,过点B作BE⊥AC于点E,以AD为边作等边三角形ADF,连接EF.(1)求证:四边形BDFE为平行四边形;(2)若AB=6,求四边形BDFE的面积.
C组培优6.如图,在▱ABCD中,E,F是对角线AC上的两点,且AE=CF,连接DE,DF,BE,BF.(1)求证:四边形BEDF是平行四边形.(2)若AD⊥DF,DF=5,AC=14,∠DAC=30°:①求线段EF的长;②求四边形BEDF的面积.
相关课件
这是一份第21讲 平行四边形课件---2024年中考数学一轮复习,共26页。PPT课件主要包含了综合模拟练,基础全练,挑战高分,中考创新练等内容,欢迎下载使用。
这是一份第21讲 平行四边形课件---2024年中考数学一轮复习,共32页。PPT课件主要包含了栏目导航,平行四边形,平行且相等,互相平分,中心对称,题型1,核心素养·推理能力,10年1考,10年4考等内容,欢迎下载使用。
这是一份专题13 平行四边形-中考数学一轮复习课件PPT,共42页。PPT课件主要包含了考点1平行四边形,平行四边形的性质,考点2平行四边形,矩形的性质,对边平行且相等,四个角是直角,相等且互相平分,矩形的判定,根据概念和定义判断,考点3菱形等内容,欢迎下载使用。









