中考数学一轮复习 课件 第34课 概率初步

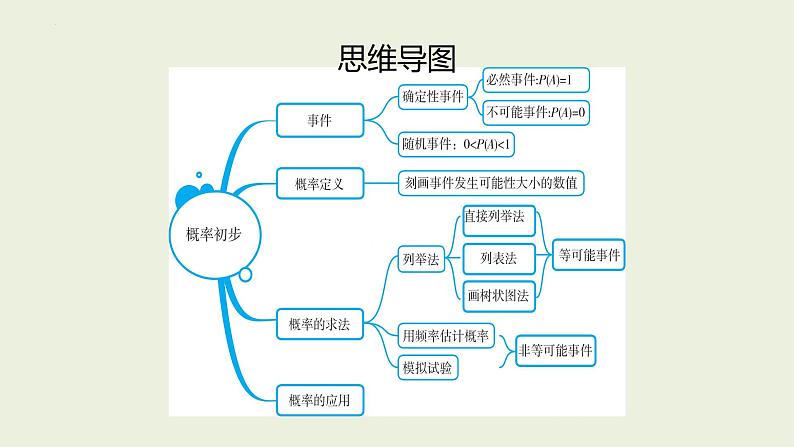
这是一份中考数学一轮复习 课件 第34课 概率初步，共35页。PPT课件主要包含了思维导图，必然会发生，必然不会发生，夯实基础，考点3用频率估计概率，中考演练，分层达标，第6题，第7题等内容，欢迎下载使用。
知识梳理1．在一定条件下，________________的事件叫做必然事件． 2．在一定条件下，________________的事件叫做不可能事件． 3．_____________________________统称确定性事件． 4．在一定条件下，可能发生也可能不发生的事件叫做不确定事件（或随机事件）．5．一般地，对于一个随机事件A，我们把刻画其发生可能性大小的数值，称为随机事件A发生的概率，记为P（A）．
必然事件与不可能事件　
考点1事件的分类与概率
点对点练习　　　　　 　　　　 　　　　 1．下列成语所描述的事件属于不可能事件的是（ ）A．水落石出B．水涨船高C．水滴石穿D．水中捞月
2．下列事件中，属于必然事件的是（ ）A．抛掷硬币时，正面朝上B．明天太阳从东方升起C．经过红绿灯路口，遇到红灯D．玩“石头、剪刀、布”游戏时，对方出“剪刀”
考点2求随机事件概率的方法
点对点练习　　　　　 　　　　 　　　　 3．第24届冬季奥林匹克运动会于2022年成功举办，某赛区设有四个冬奥会竞赛场馆，分别为：A．云顶滑雪公园；B．国家跳台滑雪中心；C．国家越野滑雪中心；D．国家冬季两项中心．小明和小颖都是志愿者，他们被随机分配到这四个竞赛场馆中的任意一个场馆的可能性相同．（1）小明被分配到国家冬季两项中心场馆做志愿者的概率是多少？（2）利用画树状图或列表的方法，求小明和小颖被分配到同一场馆做志愿者的概率．
点对点练习　　　　　 　　　　 　　　　 4．在同等条件下，某林业部门对某种幼树进行大量移植，下表是这种幼树移植过程中存活数的一组统计数据：
　估计该种幼树在此条件下移植成活的概率是________．（结果精确到0.1） 
5．如图，正方形ABCD及其内切圆O，随机地往正方形内投一粒米，落在阴影部分的概率是（ ）
【例1】近年来，洞庭湖区环境保护效果显著，南迁的候鸟种群越来越多．为了了解南迁到该区域某湿地的A种候鸟的情况，从中捕捉40只，戴上识别卡并放回；经过一段时间后观察发现，200只A种候鸟中有10只佩有识别卡，由此估计该湿地约有__________只A种候鸟．  
分析：在样本中“200只A种候鸟中有10只佩有识别卡”，即可求得有识别卡的所占比例，据此即可解答．
【变式1】当重复试验次数足够多时，可用频率来估计概率．历史上数学家皮尔逊曾在实验中掷均匀的硬币24 000次，正面朝上的次数是12 012次，频率约为0.5，则掷一枚均匀的硬币，正面朝上的概率是______．
【例2】某商场抽奖规则如下：在一只不透明的口袋中装有1个白球和2个红球，这些球除颜色外都相同，搅匀后先从中任意摸出1个球（不放回），再从余下的2个球中任意摸出1个球．（1）用树状图列出所有等可能出现的结果；（2）活动设置了一等奖和二等奖两个奖次，一等奖的获奖率低于二等奖．现规定摸出颜色不同的两球和摸出颜色相同的两球分别对应不同奖次，请写出它们分别对应的奖次，并说明理由．
解：（1）画树状图如下．
共有6种等可能出现的结果．
分析：（1）画出树状图即可；（2）由概率公式求摸出颜色不同的两球的概率和摸出颜色相同的两球的概率，进而得出结论．
【变式2】小华同学从一副扑克牌中取出花色为“红心”“黑桃”“方块”“梅花”各1张放入不透明的甲盒中，再从这副扑克牌中取出花色为“红心”“黑桃”“方块”“梅花”各1张放入不透明的乙盒中．（1）小华同学从甲盒中随机抽取1张，抽到扑克牌花色为“红心”的概率为  　； （2）小华同学从甲、乙两个盒中各随机抽取1张扑克牌．请用画树状图或列表的方法，求抽到扑克牌花色恰好是1张“红心”和1张“方块”的概率．
解：把“红心”“黑桃”“方块”“梅花”扑克牌分别记为A，B，C，D．画树状图如下．
A组基础1．下列事件中属于必然事件的是 （ ）A．任意画一个三角形，其内角和是180°B．打开电视机，正在播放新闻联播C．随机买一张电影票，座位号是奇数号D．掷一枚质地均匀的硬币，正面朝上
2．下列说法中，正确的是 （ ）A．调查某班45名学生的身高情况宜采用全面调查B．“太阳东升西落”是不可能事件C．为了直观地介绍空气各成分的百分比，最适合使用的统计图是条形统计图D．任意投掷一枚质地均匀的硬币26次，出现正面朝上的次数一定是13次
7．如图，电路图上有A，B，C3个开关和1个小灯泡，闭合开关C或同时闭合开关A，B都可以使小灯泡发亮．任意闭合其中的1个开关，小灯泡发亮的概率是  　． 
C组培优8．某校为满足学生课外活动的需求，准备开设五类运动项目，分别为A：篮球，B：足球，C：乒乓球，D：羽毛球，E：跳绳．为了解学生的报名情况，现随机抽取八年级部分学生进行调查，并根据调查结果绘制了如下两幅不完整的统计图．
请根据以上图文信息回答下列问题：（1）此次调查共抽取了多少名学生？（2）请将此条形统计图补充完整．（3）在此扇形统计图中，项目D所对应的扇形圆心角的度数为 　． （4）学生小聪和小明各自从以上五类运动项目中任选一项参加，请利用画树状图或列表的方法求他俩选择相同项目的概率．
解：（1）10÷10%=100（名），所以此次调查共抽取了100名学生．（2）C项目的人数为100－20－30－15－10=25（名）．条形统计图补充如下图．
（3）54°（4）画树状图如下．
9．课前预习是学习数学的重要环节，为了了解所教班级学生完成数学课前预习的具体情况，王老师对本班部分学生进行了为期半个月的跟踪调查，他将调查结果分为四类．A：很好；B：较好；C：一般；D：较差．并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：（1）王老师一共调查了多少名同学？（2）C类女生有　 　名，D类男生有　 　名，将条形统计图补全． 
（3）为了共同进步，王老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习，请用列表法或画树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．
C类女生有3名，D类男生有1名.