山西省长治市2023-2024学年八年级下学期期中数学试题

这是一份山西省长治市2023-2024学年八年级下学期期中数学试题，共9页。试卷主要包含了一次函数与反比例函数等内容，欢迎下载使用。

八年级数学（华东版）
注意事项：
1．本试卷共4页，满分120分，考试时间120分钟。
2．答卷前，考生务必将自己的姓名、准考证号填写在本试卷相应的位置上。
3．答卷全部在答题卡上完成，答在本试卷上无效。
4、考试结束后，将本试卷和答题卡一并交回。
第Ⅰ卷 选择题（共30分）
一、选择题（本大题共10个小题，每小题3分，共30分）
在每小题列出的四个选项中，只有一项是最符合题目要求的，请将正确选项的字母标号在答题卡相应位置涂黑．
1．在平面直角坐标系中，点在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
2．若使某个分式无意义，则这个分式可以是（ ）
A．B．C．D．
3．关于一次函数，下列说法正确的是（ ）
A．图象经过第二、三、四象限B．当时，
C．函数值随自变量的增大而减小D．图象与轴交于点
4．芯片内部有数以亿计的晶体管，为追求更高质量的芯片和更低的电力功耗，需要设计体积更小的晶体管．某品牌手机自主研发了最新型号芯片，其晶体管栅极的宽度为0.000000014米，将数据0.000000014用科学记数法表示为，其中表示的数为（ ）
A．B．C．D．
5．如图，在中，，，的平分线交于点，则的长为（ ）
A．5B．4C．3D．2
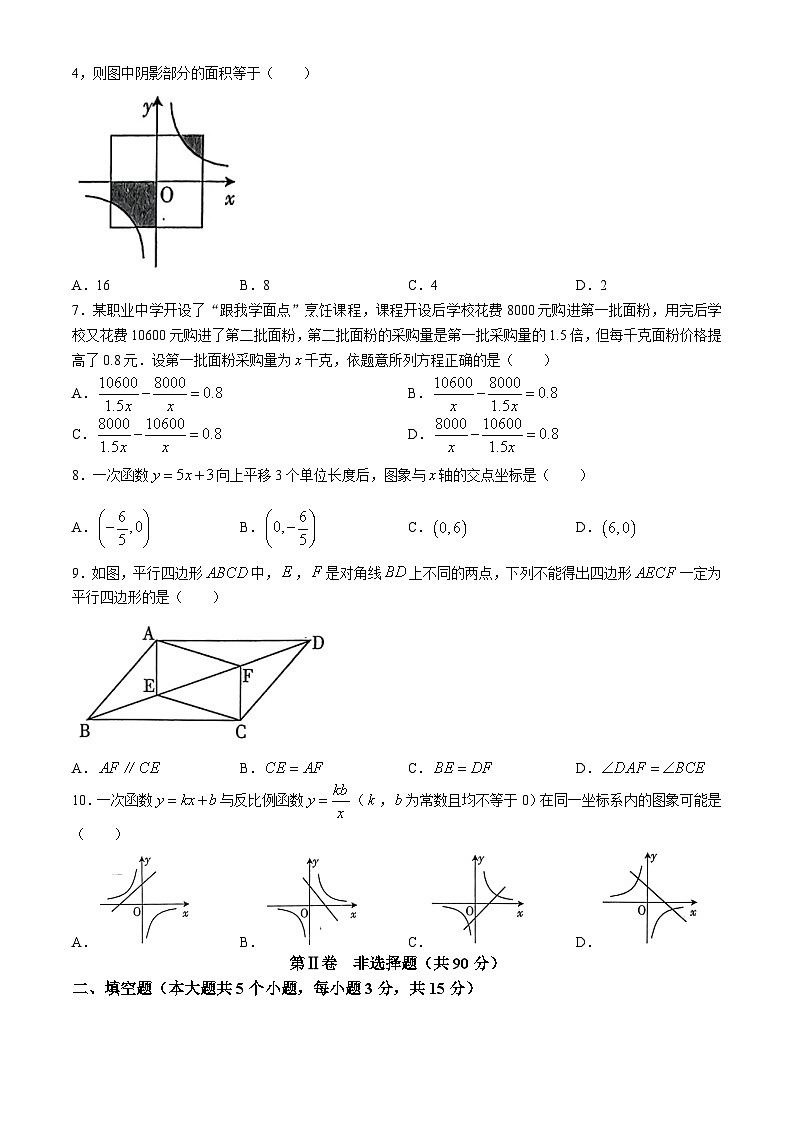
6．如图，在直角坐标系中，正方形的中心在原点，且正方形的一组对边与轴平行，若正方形的边长是4，则图中阴影部分的面积等于（ ）
A．16B．8C．4D．2
7．某职业中学开设了“跟我学面点”烹饪课程，课程开设后学校花费8000元购进第一批面粉，用完后学校又花费10600元购进了第二批面粉，第二批面粉的采购量是第一批采购量的1.5倍，但每千克面粉价格提高了0.8元．设第一批面粉采购量为千克，依题意所列方程正确的是（ ）
A．B．
C．D．
8．一次函数向上平移3个单位长度后，图象与轴的交点坐标是（ ）
A．B．C．D．
9．如图，平行四边形中，，是对角线上不同的两点，下列不能得出四边形一定为平行四边形的是（ ）
A．B．C．D．
10．一次函数与反比例函数（，为常数且均不等于0）在同一坐标系内的图象可能是（ ）
A．B．C．D．
第Ⅱ卷 非选择题（共90分）
二、填空题（本大题共5个小题，每小题3分，共15分）
11．写出一个过点且随增大而增大的一次函数表达式______．
12．若关于的分式方程（为常数）有增根，则增根是______．
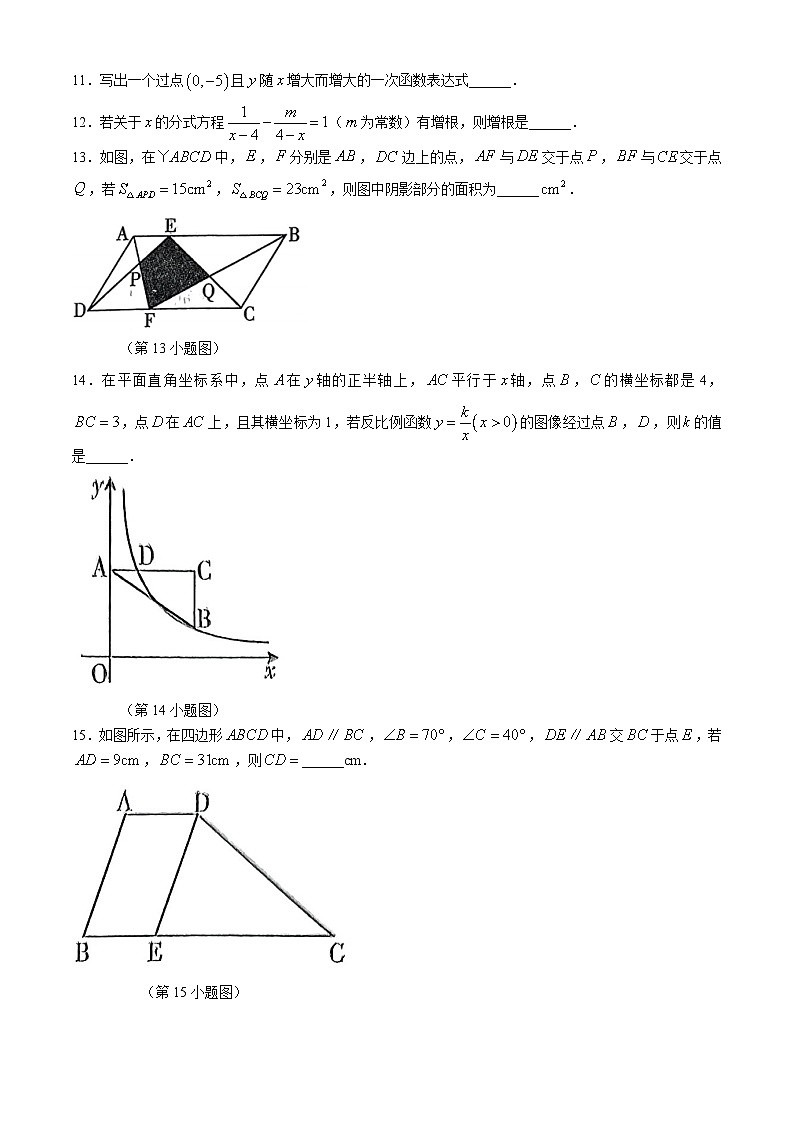
13．如图，在中，，分别是，边上的点，与交于点，与交于点，若，，则图中阴影部分的面积为______．
（第13小题图）
14．在平面直角坐标系中，点在轴的正半轴上，平行于轴，点，的横坐标都是4，，点在上，且其横坐标为1，若反比例函数的图像经过点，，则的值是______．
（第14小题图）
15．如图所示，在四边形中，，，，交于点，若，，则______cm．
（第15小题图）
三、解答题（本大题共8个小题，共75分）
解答应写出文字说明、证明过程或演算步骤．
16．（本题共2个小题，每小题5分，共10分）计算：
（1）；
（2）先化简，再求值：，其中．
17．（本题共2个小题，每小题5分，共10分）解方程：
（1）；（2）．
18．（本题7分）如图，中，点为的中点，是上的一点，且，延长至点，使得，连接．
求证：（1）；
（2）四边形是平行四边形．
19．（本题8分）茶为国饮，中国是茶的故乡和茶文化的发祥地，古时就有“神农尝百草，日遇七十二毒，得茶而解之”的传说．产自山西平定冠山的连翘茶在历史上曾是闻名遐迩的皇室贡品，2016年冠山连翘茶项目入选山西省非物质文化遗产名录．某公司采购员到茶叶市场为公司购买该种茶叶，商家推出了两种购买方式：
设该公司此次购买茶叶，按方式一购买茶叶的总费用为元，按方式二购买茶叶的总费用为元．
（1）分别求出，与之间的关系式；
（2）此采购员如何购买更优惠？
20．（本题10分）某职业学校开设了智能机器人编程的校本课程，为了更好地教学，学校购买了A，B两种型号的机器人模型．A型机器人模型单价比B型机器人模型单价多100元，用1000元购买A型机器人模型和用600元购买B型机器人模型的数量相同．
（1）求A型、B型机器人模型的单价分别是多少元？
（2）学校准备再次购买A型和B型机器人模型共20台，购买B型机器人模型不超过A型机器人模型的3倍，且商家给出了两种型号机器人模型均打八折的优惠．问购买A型和B型机器人模型各多少台时花费最少？最少花费是多少元？
21．（本题9分）世界的面食之根就在山西．山西面食，不仅是中华民族饮食文化中的重要组成部分，也是世界饮食文化中的一朵奇葩．厨师将一定质量的面团做成拉面时，面条的总长度是面条横截面面积的反比例函数，其图象经过，两点（如图）．
（1）求与之间的函数表达式；
（2）求的值，并解释它的实际意义；
（3）某厨师拉出的面条最细时的横截面面积不超过，求这根面条的总长度至少有多长．
22．（本题10分）综合与实践：
如图，已知中，对角线，交于点，过点任作直线分别交，于点，．
（第22小题图）
（1）请判断与的数量关系，并说明理由；
（2）若，，，求四边形的周长；
（3）若，，，，请直接写出的长．
23．（本题11分）综合与探究：
如图，一次函数的图象与反比例函数的图象交于点，与轴交于点，与轴交于点．
（第23小题图）
（1）求一次函数、反比例函数的表达式及点的坐标；
（2）根据图象，请直接写出关于的不等式的解集；
（3）已知为反比例函数图象上的一点，且，求点的坐标．
2023-2024学年度第二学期期中学情调研（A）
八年级数学（华东版）参考答案
一、选择题（本大题共10个小题，每小题3分，共30分）
1-5 B C D A C6-10 C A A B D
二、填空题（本大题共5个小题，每小题3分，共15分）
11、（答案不唯一）12、13、38
14、415、22
三、解答题（本大题共8个小题，共75分）
16、解：（1）原式
；
（2）原式
，
当时，原式．
17、解：（1）方程两边同时乘以得，解得，，
检验：把代入．原方程的解为：；
（2）方程两边同时乘以，得，解得：，
检验：把代入得，
是原分式方程的增根，原分式方程无解．
18、证明：（1）点为的中点，，
在和中，，，．
；
（2）由（1）证得，，，
，四边形是平行四边形．
19、解：（1）由题意得：，；
（2）当时，，解得：，
当时，，解得：，
当时，，解得：，
答：当采购员购买茶叶少于时，用购买方式二更优惠，当采购员购买茶叶等于时，两种方式都可以，当采购员购买茶叶多于时，用购买方式一更优惠．
20、解：（1）设A型机器人模型单价是元，则B型机器人模型单价是元．
根据题意，得，解这个方程，得．
经检验，是原方程的根，且符合题意．．
答：A型机器人模型单价是250元，B型机器人模型单价是150元．
（2）设购买A型机器人模型台，则购买B型机器人模型台，购买A型和B型机器人模型共花费元，
由题意得：，解得．
，即，
，随的增大而增大．
当时，，此时．
答：购买A型机器人模型5台和B型机器人模型15台时花费最少，最少花费是2800元．
21、解：（1）设与之间的函数表达式为：，
将代入可得：，
与之间的函数表达式为；
（2）点在反比例函数上，，解得：，
，且其表示的实际意义为面条的总长度为时，其横截面积为；
（3）当时，，
，随增大而减小，
当厨师拉出的面条最细时的横截面面积不超过时，这根面条的总长度至少为．
22、解：（1），理由如下：
四边形是平行四边形，，，，
在和中，，，，
，．
（2），，，
又，
四边形的周长．
（3）4．
23、解：（1）一次函数经过，，一次函数的表达式为；
一次函数经过，，，．
点在反比例函数的图象上，，反比例函数的表达式为，
当时，，解得：，；
（2）或；
（3），，，．
过点作轴于点，过点作轴于点，如图所示．
，，，
解得：．点的纵坐标为2或．
将代入得，
将代入得，点或．
会员卡费用（元/张）
茶叶价格（元/kg）
方式一：金卡会员
300
600
方式二：银卡会员
100
800