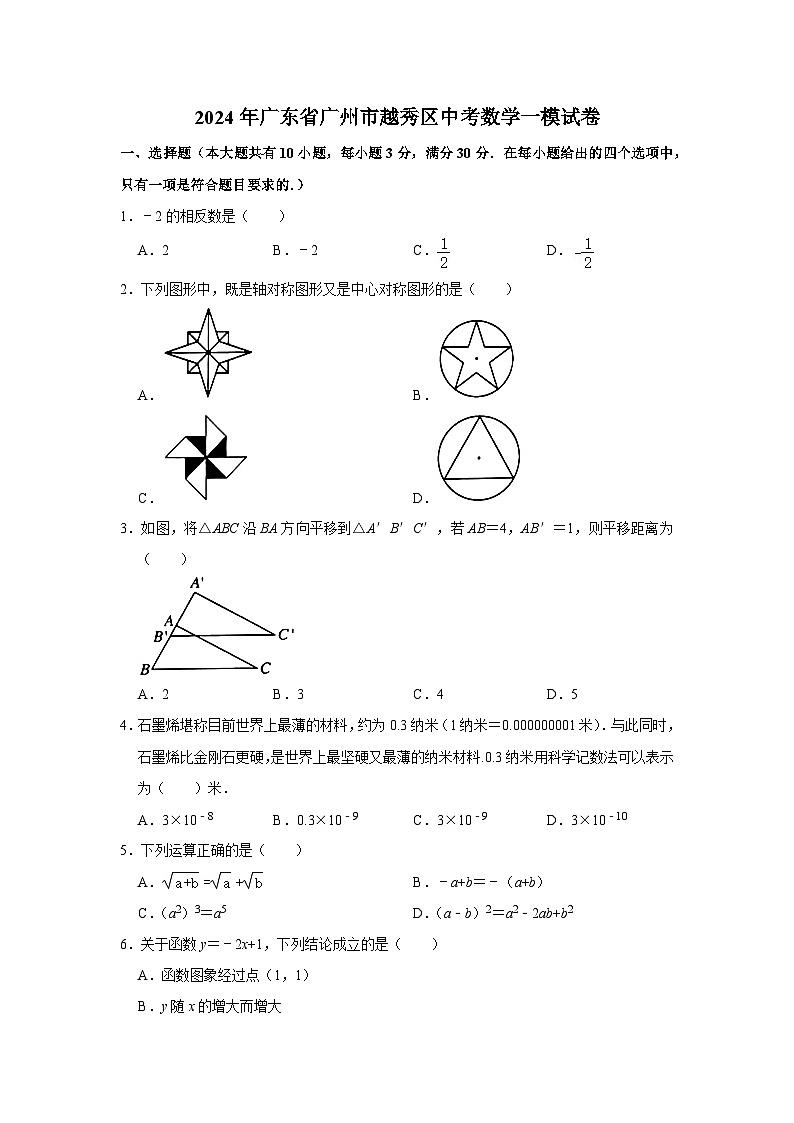
2024年广东省广州市越秀区中考数学一模试卷（附参考答案）

这是一份2024年广东省广州市越秀区中考数学一模试卷（附参考答案），文件包含2024年广东省广州市越秀区中考数学一模试卷doc、越秀区一模答案pdf等2份试卷配套教学资源，其中试卷共13页， 欢迎下载使用。
1．﹣2的相反数是（ ）
A．2B．﹣2C．D．
2．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．
C．D．
3．如图，将△ABC沿BA方向平移到△A′B′C′，若AB＝4，AB′＝1，则平移距离为（ ）
A．2B．3C．4D．5
4．石墨烯堪称目前世界上最薄的材料，约为0.3纳米（1纳米＝0.000000001米）．与此同时，石墨烯比金刚石更硬，是世界上最坚硬又最薄的纳米材料.0.3纳米用科学记数法可以表示为（ ）米．
A．3×10﹣8B．0.3×10﹣9C．3×10﹣9D．3×10﹣10
5．下列运算正确的是（ ）
A．B．﹣a+b＝﹣（a+b）
C．（a2）3＝a5D．（a﹣b）2＝a2﹣2ab+b2
6．关于函数y＝﹣2x+1，下列结论成立的是（ ）
A．函数图象经过点（1，1）
B．y随x的增大而增大
C．当x＜0时，y＞0
D．函数图象不经过第一象限
7．如图是一个正方体的平面展开图，若将其按虚线折叠成正方体后，相对面上的两个数字之和均为6，则2x﹣y+z的值为（ ）
A．0B．2C．﹣12D．20
8．某班35位同学课外阅读物的数量统计如表所示，其中有两个数据被遮盖，下列关于课外阅读物的统计量中，与被遮盖的数据无关的是（ ）
A．平均数，方差B．中位数，方差
C．平均数，众数D．中位数，众数
9．如图，点E为矩形ABCD边CD的中点，点F为边BC上一点，且∠FAE＝∠EAD，若BF＝8，FC＝2，则AF的长为（ ）
A．10B．C．12D．
10．已知二次函数y＝ax2+bx+c（a≠0）的函数值y和自变量x的部分对应取值如表所示：
若m•p＜0，则下列结论：①a＞0；②若方程ax2+bx+c＝0的两个实数根为x1，x2，则x1+x2＝1；③a+3b﹣c＜0；④n•p的最大值为．其中正确的结论是（ ）
A．①②B．②③C．③④D．②④
二、填空题（本大题共6小题，每小题3分，满分18分．）
11．使代数式有意义的x的取值范围是 ．
12．在一个不透明的布袋中装有红球、白球共40个，这些球除颜色外都相同．小明从中随机摸出一个球记下颜色并放回，通过大量重复试验，发现摸到红球的频率稳定在0.4，则布袋中红球的个数大约是 ．
13．分式方程的解是 ．
14．如图所示的衣架可以近似看成一个等腰△ABC，其中AB＝AC，∠ABC＝27°，BC＝40cm，则高AD为 cm．
（参考数据：sin27°≈0.45，cs27°≈0.89，tan27°≈0.51）
15．如图，点E为菱形ABCD的边AD上一点，且AE＝3，DE＝2，点F为对角线AC上一动点，若△DEF的周长最小值为6，则sin∠BCD＝ ．
16．如图，在△ABC中，AC＝2，BC＝1，∠ACB＝90°，点D为边AB上一动点（点D与点A，B不重合），过点D作DE⊥AC，连接CD．
（1）△CDE外接圆的直径的最小值是 ；
（2）△CDE内切圆的半径的最大值是 ．
三、解答题（本大题共9小题，满分72分．解答应写出文字说明、证明过程或演算步骤．）
17．解方程：．
18．如图，线段AC与BD相交于点O，AB∥CD，CD＝AB，求证：OC＝OA．
19．已知：．
（1）化简A；
（2）若关于x的一元二次方程x2+2ax+a+2＝0有两个相等的实数根，求A的值．
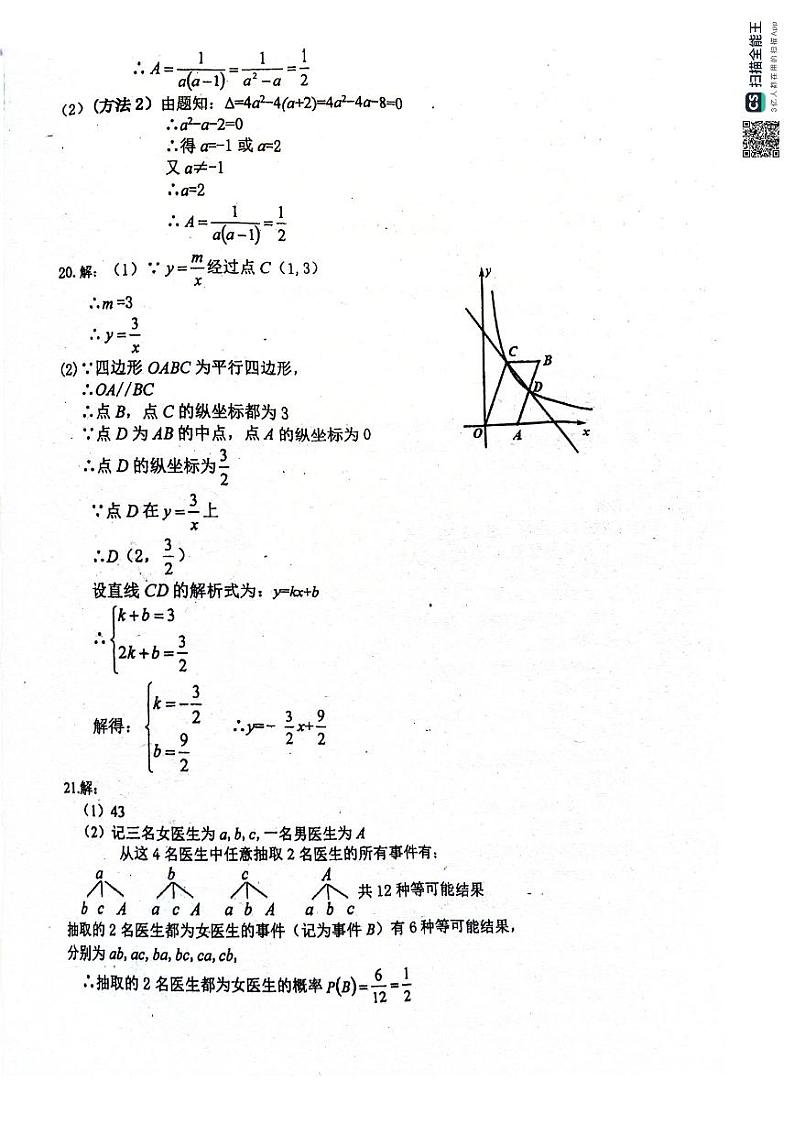
20．如图，在平面直角坐标系xOy中，点A在x轴上，四边形OABC是平行四边形，反比例函数过点C（1，3），且与边AB交于点D．
（1）求反比例函数的解析式；
（2）若点D为边AB的中点，求直线CD的解析式．
21．“英雄花开英雄城”2024广州传承弘扬红色文化系列活动正如火如荼地开展．某社区组织了形式多样的学雷锋志愿服务活动，活动现场设置义诊、科普宣传、普法宣传、消防宣传、交通宣传等多个便民服务摊位，吸引了众多市民前来参与活动．其中，前来参与义诊活动的100位市民的年龄整理可得如下的频数分布表：
（1）参与义诊活动的市民平均年龄为 岁；
（2）某医院安排了4名医生前来为市民提供义诊，现要从这4名医生（其中3名女医生，1名男医生）中随机抽调2人到附近养老院为老人义诊，用树状图或列表的方法求抽取的两名医生恰好都是女医生的概率．
22．人工智能与实体经济融合能够引领产业转型，提升人们生活品质．某科创公司计划投入一笔资金购进A，B两种型号的芯片．已知购进2片A型芯片和1片B型芯片共需900元，购进1片A型芯片和3片B型芯片共需950元．
（1）求购进1片A型芯片和1片B型芯片各需多少元？
（2）若该科创公司计划购进A，B两种型号的芯片共10万片，根据生产的需要，购进A型芯片的数量不低于B型芯片数量的4倍，问该公司如何购买芯片所需资金最少？最少资金是多少万元？
23．如图，ABCD为⊙O内接四边形，AC为⊙O的直径，，点E为上一点，且．
（1）求作点E，连接ED，延长ED，BC交于点F（尺规作图，保留作图痕迹，不写作法）；
（2）在（1）所作的图中，连接CE．
①求证：△CEF为等腰三角形；
②若FC＝5，BC＝15，求弦DE的长．
24．已知抛物线y＝﹣x2+2mx+n经过点（2，2m﹣3）．
（1）用含m的式子表示n；
（2）当m＜0时，设该抛物线与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，△ABC的外接圆与y轴交于另一点D（点D与点C不重合），求点D的坐标；
（3）若点E（﹣3，y1），F（t，y2），G（m﹣1，y3）在该抛物线上，且当3＜t≤4时，总有y1＜y2＜y3，求y3的取值范围．
25．如图，矩形ABCD中，AB＝4，，点E，F分别为边AB，BC上的点，将线段EF绕点F顺时针旋转60°，得到线段FG．射线FG与对角线AC交于点M，连接EM，EG．
（1）求∠FGE的度数；
（2）若FC＝2BF，求AM+ME﹣EB的值；
（3）连接CG，DG，若，设△CDG和△EFG的面积分别为S1，S2，当点E在边AB上运动时，求的最大值．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2024/5/1 13:13:09；用户：李乐庭；邮箱：makabaka03@xyh.cm；学号：41161924课外阅读物的数量
2
3
4
5
6
7
8
人数
■
■
9
7
9
3
2
x
…
﹣1
0
1
2
3
…
y
…
1
m
n
1
P
…
年龄分组/岁
频数
0≤x＜20
15
20≤x＜40
25
40≤x＜60
40
60≤x＜80
20