2023-2024学年天津市南开中学八年级（下）期中数学试卷（含解析）

这是一份2023-2024学年天津市南开中学八年级（下）期中数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
1.下列二次根式中，最简二次根式是( )
A. 4xB. x2+2C. 3x2D. x2
2.下列运算正确的是( )
A. 3− 3=3B. 4 5− 5=4C. 32÷ 8=4D. 3× 2= 6
3.已知直角三角形的两边长分别为3和2，则第三边长为( )
A. 5B. 13C. 1D. 5或 13
4.下列满足条件的三角形中，不是直角三角形的是( )
A. 三内角之比为1：2：3B. 三边长的平方之比为1：2：3
C. 三边长之比为3：4：5D. 三内角之比为3：4：5
5.若平行四边形中两个内角的度数比为1：2，则其中较小的内角是( )
A. 60°B. 90°C. 120°D. 45°
6.下列说法不正确的是( )
A. 两组对边分别相等的四边形是平行四边形B. 一个角是直角的平行四边形是矩形
C. 对角线互相平分且垂直的四边形是菱形D. 对角线相等的四边形是矩形
7.如图，在正方形网格中，A，B，C，D，E都是格点，则∠BAC+∠CDE的度数为( )
A. 45°
B. 40°
C. 35°
D. 30°
8.如图，阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形.已知AC=2，BC=4，则S1+S2=( )
A. 4 3B. 84πC. 2πD. 4
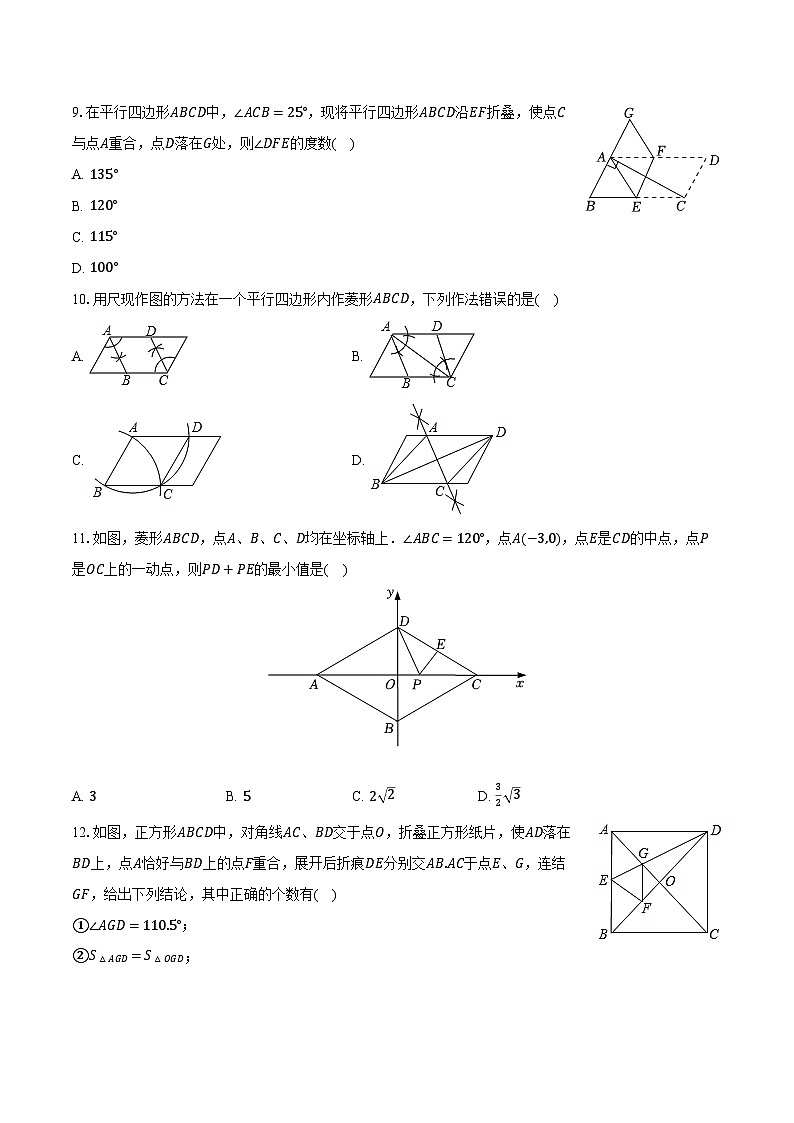
9.在平行四边形ABCD中，∠ACB=25°，现将平行四边形ABCD沿EF折叠，使点C与点A重合，点D落在G处，则∠DFE的度数( )
A. 135°
B. 120°
C. 115°
D. 100°
10.用尺现作图的方法在一个平行四边形内作菱形ABCD，下列作法错误的是( )
A. B.
C. D.
11.如图，菱形ABCD，点A、B、C、D均在坐标轴上．∠ABC=120°，点A(−3,0)，点E是CD的中点，点P是OC上的一动点，则PD+PE的最小值是( )
A. 3B. 5C. 2 2D. 32 3
12.如图，正方形ABCD中，对角线AC、BD交于点O，折叠正方形纸片，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB.AC于点E、G，连结GF，给出下列结论，其中正确的个数有( )
①∠AGD=110.5°；
②S△AGD=S△OGD；
③四边形AEFG是菱形；
④OFBF= 22．
A. 1个B. 2个C. 3个D. 4个
二、填空题：本题共6小题，每小题3分，共18分。
13.二次根式 2x+1在实数范围内有意义，则x的取值范围为______．
14.如图，正方形ODBC中，OC=1，OA=OB，则数轴上点A表示的数是______．
15.如图，E为▱ABCD的边AD上任意一点，▱ABCD的面积为6，则图中阴影部分的面积为______．
16.在平面直角坐标系中，点A(−3,6)到原点的距离为______．
17.已知：正方形ABCD的边长为8，点E、F分别在AD、CD上，AE=DF=2，BE与AF相交于点G，点H为BF的中点，连接GH，则GH的长为______．
18.如图，已知∠AED=∠ACB=90°，AC=BC=3，AE=DE=1，点D在AB上，连接CE，点M，点N分别为BD，CE的中点，则MN的长为______．
三、计算题：本大题共1小题，共8分。
19.计算：
(1) 32−4 18+2 2；
(2)( 3+ 2)2−(2+ 5)(2− 5).
四、解答题：本题共4小题，共38分。解答应写出文字说明，证明过程或演算步骤。
20.(本小题8分)
《算法统宗》是中国古代数学名著，作者是我国明代数学家程大位．在《算法统宗》中有一道“荡秋千”的问题：“平地秋千未起，踏板一尺离地．送行二步与人齐，五尺人高曾记．仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索长有几．”(注：1步=5尺)
译文：“有一架秋千，当它静止时，踏板离地1尺，将它往前推送10尺(水平距离)时，秋千的踏板就和人一样高，这个人的身高为5尺，秋千的绳索始终拉得很直，问绳索有多长．”
21.(本小题8分)
(1)已知a，b满足 2a+b−4+|a+1|=0，求(a+b)2．
(2)已知x，y为实数，且y< 2x−1+ 1−2x+2，化简： y2−4y+452−x．
22.(本小题10分)
如图，在Rt△ABC中，已知∠ABC=90°，M是边AC的中点，过点A作AN//BM，且AN=CM．
(1)求证：四边形ABMN是平行四边形；
(2)若∠BAC=30°，BC=2，求四边形ABMN的周长．
23.(本小题12分)
如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒(0GO，
∴S△AGD>S△OGD，故②错误．
∵∠AGE=∠GAD+∠ADG=67.5°=∠AED，
∴AE=AG，
又AE=FE、AG=FG，
∴AE=EF=GF=AG，
∴四边形AEFG是菱形，故③正确．
设OF=a，
∵四边形AEFG是菱形，且∠AED=67.5°，
∴∠FEG=∠FGE=67.5°，
∴∠EFG=45°，
又∠EFO=90°，
∴∠GFO=45°，
∴GF=EF= 2a，
∵∠EFO=90°，∠EBF=45°，
∴BF=EF=GF= 2a，即BF= 2OF，
∴OFBF= 22，故④正确；
故选：B．
①由四边形ABCD是正方形，可得∠GAD=∠ADO=45°，又由折叠的性质，可求得∠ADG的度数，从而求得∠AGD；
②证明△AEG≌△FEG得AG=FG，由FG>OG即可得；
③由折叠的性质与平行线的性质，易得△AEG是等腰三角形，由AE=FE、AG=FG即可得证；
④设OF=a，先求得∠EFG=45°，从而知BF=EF=GF= 2OF．
此题考查的是正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识．此题综合性较强，难度较大，注意掌握折叠前后图形的对应关系，注意数形结合思想的应用．
13.【答案】x≥−12
【解析】解：∵二次根式 2x+1在实数范围内有意义，
∴2x+1≥0，
解得x≥−12．
故答案为：x≥−12．
先根据二次根式有意义的条件列出关于x的不等式，求出x的取值范围即可．
本题考查的是二次根式有意义的条件，熟知二次根式中的被开方数是非负数是解答此题的关键．
14.【答案】− 2
【解析】解：∵OB= 12+12= 2，
∴OA=OB= 2，
∵点A在数轴上原点的左边，
∴点A表示的数是− 2，
故答案为：− 2．
在直角三角形中根据勾股定理求得OB的值，即OA的值，进而求出数轴上点A表示的数
本题考查了实数与数轴、勾股定理的综合运用．
15.【答案】3
【解析】解：∵平行四边形ABCD面积为6，
∴S△EBC=12S▱ABCD=12×6=3．
故答案为：3．
由点E是平行四边形ABCD中边AD上的任意一点，可得△EBC与▱ABCD等底等高，继而可得S△EBC=12S▱ABCD．
此题考查了平行四边形的性质．注意△EBC与▱ABCD等底等高．
16.【答案】3 5
【解析】解：过A作AB⊥x轴于B，
∵点A的坐标为(−3,6)，
∴AB=6，OB=|−3|=3，
∴OA= AB2+OB2= 62+32=3 5，
∴点A(−3,6)到原点的距离为3 5，
故答案为3 5．
过A作AB⊥x轴于B，根据坐标的定义，AB=6，OB=|−3|=3，根据勾股定理即可求得OA．
此题主要考查了点的坐标和勾股定理，准确找出B点才是解题的关键．
17.【答案】5
【解析】解：∵四边形ABCD为正方形，
∴∠BAE=∠D=90°，AB=AD，
在△ABE和△DAF中，
AB=AD∠BAE=∠DAE=DF
∴△ABE≌△DAF(SAS)，
∴∠ABE=∠DAF，
∵∠ABE+∠BEA=90°，
∴∠DAF+∠BEA=90°，
∴∠AGE=∠BGF=90°，
∵点H为BF的中点，
∴GH=12BF，
∵BC=8，CF=CD−DF=8−2=6
∴BF= BC2+CF2=10
∴GH=5
故答案为：5
根据正方形的四条边都相等可得AB=AD，每一个角都是直角可得∠BAE=∠D=90°，然后利用“边角边”证明△ABE≌△DAF得∠ABE=∠DAF，进一步得∠AGE=∠BGF=90°，从而知GH=12BF，利用勾股定理求出BF的长即可得出答案．
本题考查了正方形的性质，全等三角形的判定与性质，直角三角形两锐角互余等知识，掌握三角形全等的判定方法与正方形的性质是解题的关键．
18.【答案】 102
【解析】解：连接DN，延长DN交AC于F，连BF，
∵△ACB和△AED是等腰直角三角形，∠AED=∠ACB=90°，DE=AE，AC=BC，
∴∠EAD=∠EDA=∠BAC=45°，
∴DE/​/AC，
∴∠DEN=∠FCN，
在△DEN和△FCN中，
∠DNE=∠FNCEN=NC∠DEN=∠FCN，
∴△DEN≌△FCN(ASA)，
∴DE=FC，DN=NF，
∴AE=FC，
∵M是BD中点，
∴MN是△BDF的中位线，
∴MN=12BF，
∵∠EAD=∠BAC=45°，
∴∠EAC=∠ACB=90°，
在△CAE和△BCF中，
AC=BC∠EAC=∠FCB=90°AE=FC，
∴△CAE≌△BCF(SAS)，
∴BF=CE，
∴MN=12CE，
∵∠AED=∠ACB=90°，AC=BC=3，AE=DE=1，
∴△ADE和△ABC是等腰直角三角形，
∴∠EAD=∠BAC=45°，
∴∠EAC=90°，
∴CE= AE2+AC2= 12+32= 10，
∴MN=12CE= 102．
故答案为： 102．
延长DN交AC于F，连BF，根据DE/​/AC，可证△EDN≌△CFN，可得DE=CF，求出DN=FN，FC=ED，得出MN是中位线，再证△CAE≌△BCF，得出BF=CE，即可解题；推出∠ACE=∠CBF，求出∠CBF+∠BCE=90°，即可得出答案．
本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△EDN≌△CFN和△CAE≌△BCG是解题的关键．
19.【答案】解：(1) 32−4 18+2 2
=4 2− 2+ 2
=4 2；
(2)( 3+ 2)2−(2+ 5)(2− 5)
=3+2 6+2−4+5
=6+2 6．
【解析】本题考查了二次根式的混合运算，准确熟练地进行计算是解题的关键．
(1)先把每一个二次根式化成最简二次根式，然后再进行加减计算即可；
(2)利用平方差公式和完全平方公式，即可解答．
20.【答案】解：设绳索有x尺长，
由题意得：102+(x+1−5)2=x2，
解得：x=14.5，
即绳索长14.5尺．
【解析】本题考查了勾股定理的应用，理解题意，由勾股定理得出方程是解题的关键．设绳索有x尺长，由勾股定理得出方程，解方程即可．
21.【答案】解：(1) 2a+b−4+|a+1|=0，
∵2a+b−4≥0，a+1≥0，
∴2a+b−4=0，a+1=0，
∴a=−1，b=6，
∴(a+b)2=(−1+6)2=25；
(2)y< 2x−1+ 1−2x+2，
∵2x−1≥0，1−2x≥0，
∴2x−1=0，
解得，x=12，
∴y