






还剩19页未读,
继续阅读
所属成套资源:全套粤教版高中物理选择性必修第三册课时教学课件
成套系列资料,整套一键下载
粤教版高中物理选择性必修第三册第2章素养提升课1气体实验定律的综合应用课件
展开
这是一份粤教版高中物理选择性必修第三册第2章素养提升课1气体实验定律的综合应用课件,共27页。
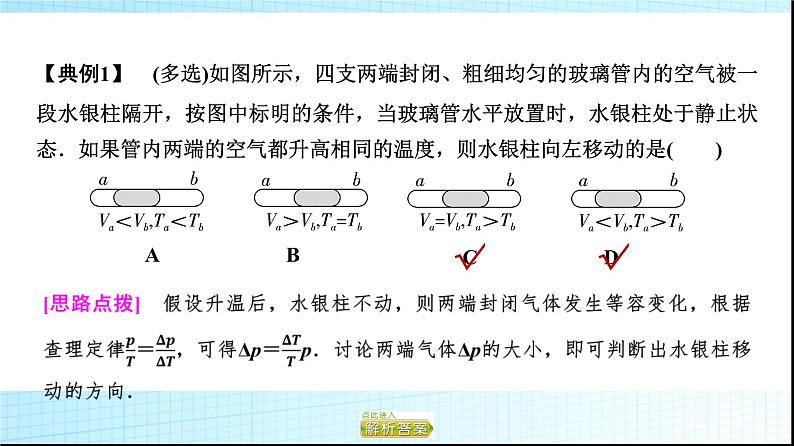
第二章 气体、液体和固体素养提升课(一) 气体实验定律的综合应用关键能力·情境探究达成01考点1 液柱类移动问题考点2 关联气体问题考点3 理想气体图像转换问题考点1 液柱类移动问题此类问题的特点是:当气体的压强、体积及温度都发生变化时,直接判定液柱或活塞的移动方向比较困难,那么处理这类问题一般有以下几种方法. 2.图像法判断液柱移动还可用图像法,设液柱下方的气体压强为p1,液柱上方的气体压强为p2,则在同一p-T坐标系中画出两段气柱的等容线,如图所示,在温度相同时p1>p2,得气柱1等容线的斜率较大,当两气柱升高相同的温度ΔT时,其压强的增量Δp1>Δp2,液柱上移.3.极限法对上部的气体压强p2进行极限推理,认为p2→0,上部为真空,升温时,下部气体的压强p1增大,液柱上移.[特别提醒] 此类问题中,若是气体温度降低,则ΔT为负值,Δp也为负值,表示气体压强减小,那么降温后液柱应向压强减小多的一侧移动.【典例1】 (多选)如图所示,四支两端封闭、粗细均匀的玻璃管内的空气被一段水银柱隔开,按图中标明的条件,当玻璃管水平放置时,水银柱处于静止状态.如果管内两端的空气都升高相同的温度,则水银柱向左移动的是( )A BC D √√ √[跟进训练]1.如图所示,左端封闭、右侧开口的U形管内分别用水银封有两部分气体,右侧部分封闭气体的压强为p1,水银面高度差为h.当左侧部分气体温度升高较小的Δt,重新达到平衡后,h和p1的变化是( )A.h不变,p1不变 B.h不变,p1变大C.h变小,p1变小 D.h变小,p1不变 考点2 关联气体问题该类问题涉及两部分(或两部分以上)的气体,它们之间虽然没有气体交换,但在压强或体积这些量间有一定的关系,分析清楚这些关系往往是解决问题的关键,解决这类问题的一般方法有:(1)分别选取每一部分气体为研究对象,确定初末状态及其状态参量,根据气体实验定律或理想气体状态方程写出状态量间的关系式.(2)分析关联气体之间的压强关系、体积关系,并写出关系式.(3)联立多个方程求解. [答案] (1)2.5×105 Pa (2)1 200 K关联气体问题的解题关键(1)根据两部分气体的关联情况,找出两部分气体关联物理量之间的关系.(2)分别对两部分气体依据特点找出各自遵循的规律,写出相应的方程.[跟进训练]2.如图所示,容积均为V的气缸A、B下端有细管(容积可忽略)连通,阀门K2位于细管的中部,A、B的顶部各有一阀门K1、K3,B中有一可自由滑动的活塞(质量、体积均可忽略).初始时,三个阀门均打开,活塞在B的底部;关闭K2、K3,通过K1给气缸充气,使A中气体的压强达到大气压p0的3倍后关闭K1.已知室温为27 ℃,气缸导热.(1)打开K2,求稳定时活塞上方气体的体积和压强; (2)接着打开K3,求稳定时活塞的位置; [答案] 在气缸B的顶部 (3)再缓慢加热气缸内气体使其温度升高20 ℃,求此时活塞下方气体的压强. [答案] 1.6p0考点3 理想气体图像转换问题1.准确理解p -V图像、p -T图像和V-T图像的特点、函数关系和物理意义.2.知道图线上的一个点表示的是一定质量气体的一个平衡状态,知道其状态参量p、V、T.3.知道图线上的某一线段表示的是一定质量的气体由一个平衡状态( p、V、T)转化到另一个平衡状态( p′、V′、T′)的过程,并能判断出该过程是否是等温过程、等容过程或等压过程.4.从图像中的某一点(平衡状态)的状态参量开始,根据不同的变化过程,先用相对应的规律计算出下一点(平衡状态)的状态参量,再逐一分析计算出各点的p、V、T.5.根据计算结果在图像中描点、连线,作出一个新的图线,并根据相应的规律逐一检查是否有误.【典例3】 如图所示是一定质量的理想气体状态按图中箭头顺序变化,状态D的温度为27 ℃,BC为一段双曲线,试求出TA、TB、TC,并画出气体状态变化的p -T图像.(T=273 K+t)[思路点拨] 对于某一物理现象或物理变化过程,可能表现为多个物理量与同一物理量间均存在变化关系,此种情况下可进行图像转化.转化时一定要抓住同一时刻或同一状态转化量所具有的特点,利用两者的相互对应性确定转化的图像,当然还有些复杂的问题,需要利用相关的物理规律确定转化量间的函数关系才能解决. [答案] 300 K 600 K 600 K p -T图像见解析应用理想气体图像分析相关问题的关键点(1)图像上的一个点表示一定质量气体的一个平衡状态,它对应着三个状态参量.(2)图像上的某一条直线或曲线表示一定质量的气体状态变化的一个过程.√[跟进训练]3.如图所示,一定质量的理想气体,从状态1出发经过状态2和3,最终又回到状态1.那么,在下列的p-T图像中,反映了上述循环过程的是( )A BC DB [从状态1出发经过状态2和3,最终又回到状态1,先后经历了等压膨胀、等容降温、等温压缩三个变化过程,由此判断B项正确.]
第二章 气体、液体和固体素养提升课(一) 气体实验定律的综合应用关键能力·情境探究达成01考点1 液柱类移动问题考点2 关联气体问题考点3 理想气体图像转换问题考点1 液柱类移动问题此类问题的特点是:当气体的压强、体积及温度都发生变化时,直接判定液柱或活塞的移动方向比较困难,那么处理这类问题一般有以下几种方法. 2.图像法判断液柱移动还可用图像法,设液柱下方的气体压强为p1,液柱上方的气体压强为p2,则在同一p-T坐标系中画出两段气柱的等容线,如图所示,在温度相同时p1>p2,得气柱1等容线的斜率较大,当两气柱升高相同的温度ΔT时,其压强的增量Δp1>Δp2,液柱上移.3.极限法对上部的气体压强p2进行极限推理,认为p2→0,上部为真空,升温时,下部气体的压强p1增大,液柱上移.[特别提醒] 此类问题中,若是气体温度降低,则ΔT为负值,Δp也为负值,表示气体压强减小,那么降温后液柱应向压强减小多的一侧移动.【典例1】 (多选)如图所示,四支两端封闭、粗细均匀的玻璃管内的空气被一段水银柱隔开,按图中标明的条件,当玻璃管水平放置时,水银柱处于静止状态.如果管内两端的空气都升高相同的温度,则水银柱向左移动的是( )A BC D √√ √[跟进训练]1.如图所示,左端封闭、右侧开口的U形管内分别用水银封有两部分气体,右侧部分封闭气体的压强为p1,水银面高度差为h.当左侧部分气体温度升高较小的Δt,重新达到平衡后,h和p1的变化是( )A.h不变,p1不变 B.h不变,p1变大C.h变小,p1变小 D.h变小,p1不变 考点2 关联气体问题该类问题涉及两部分(或两部分以上)的气体,它们之间虽然没有气体交换,但在压强或体积这些量间有一定的关系,分析清楚这些关系往往是解决问题的关键,解决这类问题的一般方法有:(1)分别选取每一部分气体为研究对象,确定初末状态及其状态参量,根据气体实验定律或理想气体状态方程写出状态量间的关系式.(2)分析关联气体之间的压强关系、体积关系,并写出关系式.(3)联立多个方程求解. [答案] (1)2.5×105 Pa (2)1 200 K关联气体问题的解题关键(1)根据两部分气体的关联情况,找出两部分气体关联物理量之间的关系.(2)分别对两部分气体依据特点找出各自遵循的规律,写出相应的方程.[跟进训练]2.如图所示,容积均为V的气缸A、B下端有细管(容积可忽略)连通,阀门K2位于细管的中部,A、B的顶部各有一阀门K1、K3,B中有一可自由滑动的活塞(质量、体积均可忽略).初始时,三个阀门均打开,活塞在B的底部;关闭K2、K3,通过K1给气缸充气,使A中气体的压强达到大气压p0的3倍后关闭K1.已知室温为27 ℃,气缸导热.(1)打开K2,求稳定时活塞上方气体的体积和压强; (2)接着打开K3,求稳定时活塞的位置; [答案] 在气缸B的顶部 (3)再缓慢加热气缸内气体使其温度升高20 ℃,求此时活塞下方气体的压强. [答案] 1.6p0考点3 理想气体图像转换问题1.准确理解p -V图像、p -T图像和V-T图像的特点、函数关系和物理意义.2.知道图线上的一个点表示的是一定质量气体的一个平衡状态,知道其状态参量p、V、T.3.知道图线上的某一线段表示的是一定质量的气体由一个平衡状态( p、V、T)转化到另一个平衡状态( p′、V′、T′)的过程,并能判断出该过程是否是等温过程、等容过程或等压过程.4.从图像中的某一点(平衡状态)的状态参量开始,根据不同的变化过程,先用相对应的规律计算出下一点(平衡状态)的状态参量,再逐一分析计算出各点的p、V、T.5.根据计算结果在图像中描点、连线,作出一个新的图线,并根据相应的规律逐一检查是否有误.【典例3】 如图所示是一定质量的理想气体状态按图中箭头顺序变化,状态D的温度为27 ℃,BC为一段双曲线,试求出TA、TB、TC,并画出气体状态变化的p -T图像.(T=273 K+t)[思路点拨] 对于某一物理现象或物理变化过程,可能表现为多个物理量与同一物理量间均存在变化关系,此种情况下可进行图像转化.转化时一定要抓住同一时刻或同一状态转化量所具有的特点,利用两者的相互对应性确定转化的图像,当然还有些复杂的问题,需要利用相关的物理规律确定转化量间的函数关系才能解决. [答案] 300 K 600 K 600 K p -T图像见解析应用理想气体图像分析相关问题的关键点(1)图像上的一个点表示一定质量气体的一个平衡状态,它对应着三个状态参量.(2)图像上的某一条直线或曲线表示一定质量的气体状态变化的一个过程.√[跟进训练]3.如图所示,一定质量的理想气体,从状态1出发经过状态2和3,最终又回到状态1.那么,在下列的p-T图像中,反映了上述循环过程的是( )A BC DB [从状态1出发经过状态2和3,最终又回到状态1,先后经历了等压膨胀、等容降温、等温压缩三个变化过程,由此判断B项正确.]
相关资料
更多









