






初中数学3 正方形的性质与判定课文ppt课件
展开1.通过阅读课本,掌握正方形的判定定理,会运用平行四边形、矩形、菱形、正方形的判定方法进行有关的证明和计算,发展学生演绎推理的能力.2.经历探究正方形的判定定理的过程,发展学生主动探究的学习习惯、综合推理的能力,逐步掌握说理的基本方法,培养积极探索、勇于创新的精神,以及推陈出新的创新能力.3.通过借助多媒体软件的展示直观感受、合作交流、师生互动,发现数学中蕴涵的美,激发学 生学习的自觉性、积极性,提高学习数学的兴趣,进一步发展学生合作交流的能力和数学表达能力.
1.正方形的定义是什么?2.正方形的性质有哪些?
(有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形)
(正方形的四个角都是直角,四条边相等;正方形的对角线相等且互相垂直平分,并且每条对角线平分一组对角;两条对角线将正方形分成四个全等的等腰直角三角形,正方形是轴对称图形,有四条对称轴)
宁宁在商场看中了一块方形纱巾,但不知是否是正方形,只见销售员阿姨拉起纱巾的一组对角能完全重合,看宁宁还在犹豫,又拉起纱巾的另一组对角,只见另一组对角也能完全重合,认为是正方形,把纱巾给了宁宁.你认为手上的纱巾一定是正方形吗?
问题2 如图,某一拉门在完全关闭时,其相应的菱形变成正方形.请说 说图中∠1的变化过程.
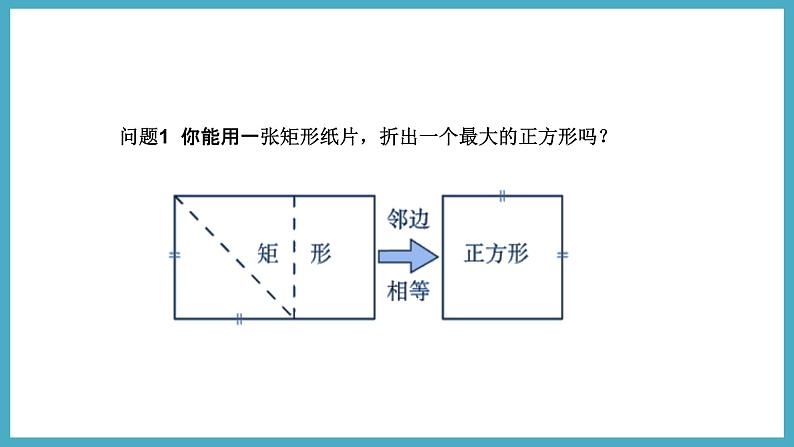
问题1 你能用一张矩形纸片,折出一个最大的正方形吗?
1.请同学们阅读课本22-23 页内容.2.将一张长方形纸对折两次,然后剪下一个角,打开,怎样剪才能 剪出一个正方形?
自主探究 (10min)
(因为正方形的两条对角线把它分成四个全等的等腰直角三角形,把折痕作对角线,这时只需剪一个等腰直角三角形,打开即是正方形,因此只要保证剪口线与折痕成45°角即可)
3.满足什么条件的矩形是正方形? 满足什么条件的菱形是正方形?
(有一组邻边相等的矩形是正方形;对角线互相垂直的矩形是正方形.有一个角是直角的菱形是正方形;对角线相等的菱形是正方形)
①猜想:菱形的中点四边形会是什么形状?②猜想:矩形的中点四边形会是什么形状?
(菱形的中点四边形是矩形)
(矩形的中点四边形是菱形)
请尝试证明这两个猜想.
【证明 】①已知:如图①,四边形ABCD是菱形,点 E,F,G,H分别是 AB,BC,CD,AD的中点.求证:四边形 EFGH为矩形.证明:连接AC,BD,∵ E,F 分别是AB 和BC 的中点,∴EF∥AC.同理可证 HG∥AC,EH∥BD,FG∥BD.∴EF∥HG,EH∥FG,∴四边形 EFGH为平行四边形.∵四边形 ABCD 是菱形,∴AC⊥BD,∴EH⊥EF,∴∠HEF=90°.∴四边形 EFGH 是矩形.
提疑惑:你有什么疑惑?
【知识点 1】正方形的判定正方形常用的判定定理:有一组邻边相等的矩形是正方形; 对角线互相垂直的矩形是正方形; 有一个角是直角的菱形是正方形; 对角线相等的菱形是正方形.注意:平行四边形、矩形、菱形、正方形四者之间的关系(如图所示).
【知识点2】顺次连接特殊的四边形各边中点得到的四边形的形状(1)顺次连接四边形各边中点得到的四边形是平行四边形.(2)顺次连接矩形各边中点得到的四边形是菱形.(3)顺次连接菱形各边中点得到的四边形是矩形.(4)顺次连接正方形各边中点得到的四边形是正方形.要求: 新四边形由原四边形各边中点顺次连接而成. (1)若原四边形的对角线互相垂直,则新四边形是矩形. (2)若原四边形的对角线相等,则新四边形是菱形. (3)若原四边形的对角线垂直且相等,则新四边形是正方形.
例 1: 下列命题正确的是( ) A.正多边形的外角和为 360° B.对角线相等的四边形是矩形 C.等边三角形是中心对称图形 D.对角线相等且互相垂直的四边形是正方形
【题型一】正方形的判定简单应用
例 2 下列命题正确的是( )A.对角线相等的平行四边形是正方形B.对角线互相垂直且相等的四边形是矩形C.顺次连接菱形各边中点所得的四边形是正方形D.菱形的面积为两条对角线长度乘积的一半
例3: 如图,E,F,M,N 分别是正方形ABCD 四条边上的点,且 AE=BF=CM=DN,连接EF,FM,MN,EN.求证:四边形 EFMN是正方形.
【题型二】利用正方形的判定方法进行简单说明
证明: ∵四边形 ABCD是正方形,∴AB=BC=CD=AD,∠A=∠B=∠C=∠D=90°.∵AE=BF=CM=DN,∴AN=DM=CF=BE.∴△ANE≌△DMN≌△CFM≌△BEF.∴EF=EN=NM=MF,∠ENA=∠DMN.∴四边形 EFMN 是菱形.∵∠DMN+∠DNM=90°,∴∠ENA+∠DNM=90°.∴∠ENM=90°.∴四边形 EFMN是正方形.
例 4:如图,在菱形ABCD中,对角线AC,BD 相交于点O,点 E,F 在对角线BD 上,且BE=DF,AE⊥AF.求证:四边形 AECF 是正方形.
证明:∵四边形 ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD.∵BE=DF,∴OB-BE=OD-DF,即OE=OF.又∵OA=OC,∴四边形 AECF是平行四边形.∵AC⊥EF,∴四边形AECF是菱形.∵AE⊥AF,∴∠EAF=90°,∴四边形 AECF是正方形.
【题型三】根据正方形的性质与判定求线段的长度
例5: 如图,在矩形纸片 ABCD 中,AB=6cm,BC=9cm.现将其沿 AE折叠,使得点 B落在边AD 上的点 F 处,折痕与边 BC 交于点 E,则 CE 的长为( )A.6 cm B.4cm C.3cm D.2cm
初中数学北师大版九年级上册4 探索三角形相似的条件示范课ppt课件: 这是一份初中数学北师大版九年级上册<a href="/sx/tb_c99904_t3/?tag_id=26" target="_blank">4 探索三角形相似的条件示范课ppt课件</a>,共15页。PPT课件主要包含了旧知回顾,自主探究,小组讨论,小组展示,我提问,我回答,我补充,我质疑,越展越优秀,教师讲评等内容,欢迎下载使用。
北师大版九年级上册4 探索三角形相似的条件评课课件ppt: 这是一份北师大版九年级上册<a href="/sx/tb_c99904_t3/?tag_id=26" target="_blank">4 探索三角形相似的条件评课课件ppt</a>,共14页。PPT课件主要包含了我提问,我回答,我补充,我质疑,越展越优秀等内容,欢迎下载使用。
北师大版九年级上册3 正方形的性质与判定示范课ppt课件: 这是一份北师大版九年级上册<a href="/sx/tb_c99892_t3/?tag_id=26" target="_blank">3 正方形的性质与判定示范课ppt课件</a>,文件包含131正方形的性质pptx、131mp4等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。













