






初中数学北师大版九年级上册6 应用一元二次方程教案配套课件ppt
展开1.通过阅读课本可以根据实际面积问题中的等量关系列出方程,提高学生的应用意识2.通过归类面积问题的题型,构建解决面积问题的数学模型,发展学生的建模能力.3.经历分析具体问题中的数量关系、建立方程模型并解决问题的过程,进一步体会方程是刻画现实世界中数量关系的一个有效的数学模型.
1.列方程解应用题的一般步骤是什么?2.解应用题的注意点是什么?
(审、设、列、解、验、答)
还记得本章开始时梯子下滑的问题吗? 在这个问题中,如果梯子长度是13米,下滑前梯子顶端与地面的垂直距离为12米,那么梯子顶端下滑的距离与梯子底端滑动的距离可能相等吗?如果相等,那么这个距离是多少? 怎么设未知数?在这个问题中存在怎样的等量关系?如何利用勾股定理来列方程?
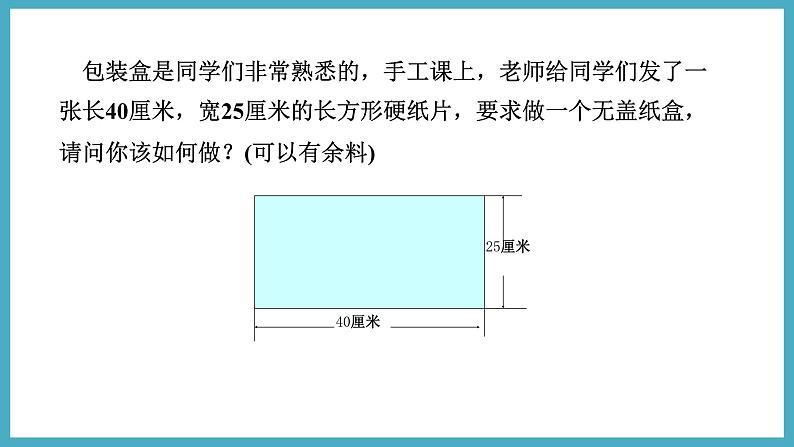
包装盒是同学们非常熟悉的,手工课上,老师给同学们发了一张长40厘米,宽25厘米的长方形硬纸片,要求做一个无盖纸盒,请问你该如何做?(可以有余料)
提起代数,大家会想到什么?事实上,过去代数的中心问题就是对方程的研究,特别是对方程解法的研究.下面是我国南宋数学家杨辉提出的一个问题:“直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),阔及长各几步?”大家试试解决这个问题.
1.请同学们阅读课本52-53页内容并思考.2.阅读教材52页例1,找出问题中合适的等量关系,设适当的未知数列方程.3.探究应用一元二次方程解应用题的一般步骤.
(列方程解应用题的一般步骤:(1)审题.(2)设未知数.(3)列方程.(4)解方程.(5)验根.(6)作答)
4.有时求解一元二次方程会产生两个不相等的实数根,如何判断哪一个根符合要求或者是两个根能够同时符合要求呢?
(需要根据实际问题判断根的合理性,再根据问题的实际意义对根进行取舍)
如图,在宽为20 m,长为32 m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪 的面积为540 m²,求道路的宽度.(尝试用不同的方法表示出草坪面积)
解: 设道路的宽度为x m.(1)20×32-20x-32x+x²=540;(2)(20-x)·(32-x)=540.整理得x²-52x+100=0,解得x₁=50(舍去),x₂=2.答:道路的宽度为 2 m .
提疑惑:你有什么疑惑?
知识点 2:动态几何问题(难点)1.关键:“以静代动”,把动的点进行转换,用时间表示长度.2.方法:时间变路程.3.求“动点的运动时间”可以转化为求“动点的运动路程”,也就是求线段的长度.4.常找的数量关系——面积、勾股定理等.
知识点3:建立一元二次方程的模型解应用题的一般步骤(重点)1.步骤:①审:审题,分清题意,明确题目要求,弄清已知数、未知数以及它们之间的关系;②设:设未知数,方法有直接设未知数法和间接设未知数法两种;③列:根据题中的等量关系列方程;④解:求出所列方程的解;⑤验:检验解是否符合题意;⑥答:回答题目中要解决的问题.
2.注意事项:(1)在一道应用题中,往往含有几个未知量,应恰当地选择其中的一个用字母x表示,然后根据各量之间的数量关系,将其他几个量用含x的代数式表示出来.(2)设未知数时必须写清单位、用对单位.作答时必须写上单位.(3)一定要对方程的根加以检验,看它是否符合实际意义.
例1:公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图中阴影部分),原空地一边减少了1 m,另一边减少了2 m,剩余空地的面积为18 m²,求原正方形空地的边长.设原正方形空地的边长为x m,则可列方程为( ) A.(x-1)(x-2)=18 B.x²-3x+16=0 C.(x+1)(x+2)=18 D.x²+3x+16=0
例2:如图,在宽为20 m,长为30 m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为551 m²,则道路的宽为 m.
点拨:设道路的宽为x m,根据题意得20×30-20x-30x+x²=551,解得x₁=1,x₂=49(不合题意,舍去),∴道路的宽为1 m.
例3:如图,若要建一个矩形养鸡场,养鸡场的一边靠墙,另三边用竹篱笆围成,墙对面有一个2 米宽的门,篱笆总长36 米.(1)若墙长为18 米,围成养鸡场的面积为180 平方米,则养鸡场的长和宽各为多少米?
解:(1)设 AB为x 米,根据题意得x(36-2x+2)=180,解得x₁=10,x₂=9,当x=10时,36-2x+2=18,符合题意.当x=9时,36-2x+2=20>18,不符合题意,舍去,则养鸡场的宽为 10 米,长为 18 米.
例3:如图,若要建一个矩形养鸡场,养鸡场的一边靠墙,另三边用竹篱笆围成,墙对面有一个2米宽的门,篱笆总长36米.(2)围成养鸡场的面积可能达到200平方米吗?
(2)设 AB为y米,根据题意得y(36-2y+2)=200,整理得y²-19y+100=0,∵Δ=(-19)²-4×100=361-400<0,∴方程没有实数根,∴围成养鸡场的面积不能达到200 平方米.
变式: 如图,矩形 ABCD中,AB=6 厘米,BC=12厘米,点 P 从点 A 开始沿AB 边向点 B 以 1厘米/秒的速度移动,点 Q从点 B 开始沿BC 边向点C 以2 厘米/秒的速度移动,如果 P、Q分别从A、B同时出发,其中一点到达终点后两点均停止运动.(1)经过几秒,△PBQ的面积等于8平方厘米?
九年级上册4 探索三角形相似的条件评课ppt课件: 这是一份九年级上册<a href="/sx/tb_c99904_t3/?tag_id=26" target="_blank">4 探索三角形相似的条件评课ppt课件</a>,文件包含444黄金分割pptx、444黄金分割avi等2份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
北师大版九年级上册1 成比例线段教案配套ppt课件: 这是一份北师大版九年级上册<a href="/sx/tb_c99901_t3/?tag_id=26" target="_blank">1 成比例线段教案配套ppt课件</a>,文件包含412等比性质pptx、412等比性质经典浓度问题mp4等2份课件配套教学资源,其中PPT共15页, 欢迎下载使用。
初中数学北师大版九年级上册1 用树状图或表格求概率课文内容课件ppt: 这是一份初中数学北师大版九年级上册<a href="/sx/tb_c99917_t3/?tag_id=26" target="_blank">1 用树状图或表格求概率课文内容课件ppt</a>,文件包含313“配紫色”游戏pptx、配紫色游戏mp4等2份课件配套教学资源,其中PPT共21页, 欢迎下载使用。













