初中数学北师大版九年级上册4 探索三角形相似的条件示范课ppt课件

这是一份初中数学北师大版九年级上册4 探索三角形相似的条件示范课ppt课件，共15页。PPT课件主要包含了旧知回顾，自主探究，小组讨论，小组展示，我提问，我回答，我补充，我质疑，越展越优秀，教师讲评等内容，欢迎下载使用。

1.通过阅读课本学生自主探究三角形相似的判定和边角的关系，培养学生的总结能力；2.通过自主学习和合作交流，学生能理解相似三角形的判定定理 2，培养学生的几何直观能力；3.通过教师讲评，学生会利用相似三角形的判定定理 2 证明及解决相关题目，培养学生分析问题和解决问题的能力.
1.相似三角形的定义是什么？（三个角分别相等，三边对应成比例的两个三角形叫做相似三角形）2.相似三角形的判定定理1是什么？（两角分别相等的两个三角形相似）
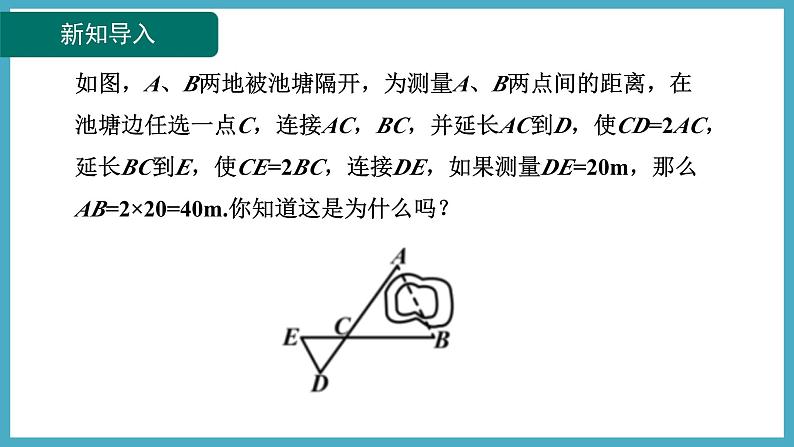
如图，A、B两地被池塘隔开，为测量A、B两点间的距离，在池塘边任选一点C，连接AC，BC，并延长AC到D，使CD=2AC，延长BC到E，使CE=2BC，连接DE，如果测量DE=20m，那么AB=2×20=40m.你知道这是为什么吗？
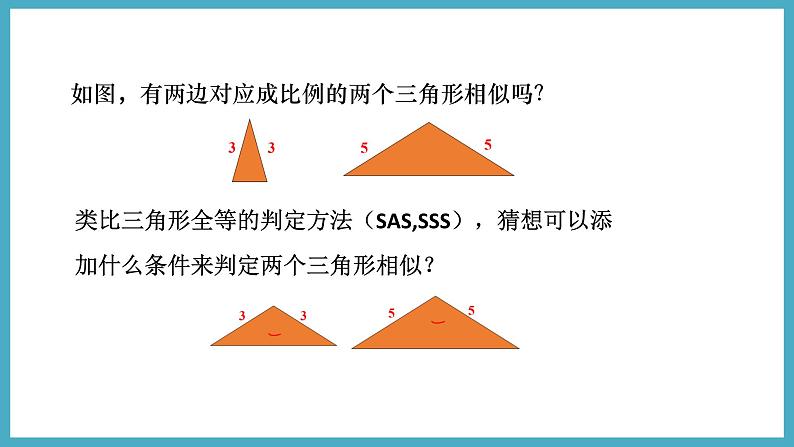
如图，有两边对应成比例的两个三角形相似吗？
类比三角形全等的判定方法（SAS,SSS），猜想可以添加什么条件来判定两个三角形相似？
1.请同学们阅读课本91-92页，勾画重点内容.2.请同学们动手完成91页的做一做.3.请同学们在完成上面任务后思考以下问题：①两个三角形有两边成比例，它们一定相似吗？（不一定）②如果两个三角形有两边成比例，且有一个角相等，它们一定相似吗？如何规定相等的这个角能确定这两个三角形一定相似？（不一定；规定相等的角是成比例的两边的夹角）
已知：如图，O为△ABC内一点，A'，B'分别是OA，OB上的点，且OA'：AA'=OB'：BB'=1：2.求证：△OA'B'∽△OAB.
证明:∵OA': AA'=OB': BB'=1:2,∴OA':OA=OB':OB=1:3,∵∠A'OB'=∠AOB,∴△OA'B'∽△OAB.
提疑惑：你有什么疑惑？
知识点：判定定理 2如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似.可以简单说成“两边成比例且夹角相等的两个三角形相似”.
例1：如图，若P为△ABC的边AB上一点（AB>AC），则下列条件不能判定△ABC∽△ACP 的是（ ）
【题型一】相似三角形的判定
例2：如图，小正方形的边长均为1，则下列选项的三角形（阴影部分）与△ABC 相似的是（ ）
【题型三】利用相似三角形求线段长度例 4: 如图,在直角坐标系中,已知点 A(2,0),B(0,4),在 x轴上找到点 C(1,0),y轴的正半轴上找到点 D,使△AOB 与△DOC 相似,则点 D的坐标是_______________.
本节课我们学习了用边角关系判定两三角形相似，主要知识有：1.判定定理2的内容是什么？（两边成比例且夹角相等的两个三角形相似）2.如何利用判定定理 2 证明？（找两个三角形的两条对应边成比例，并且两条边的夹角相等）