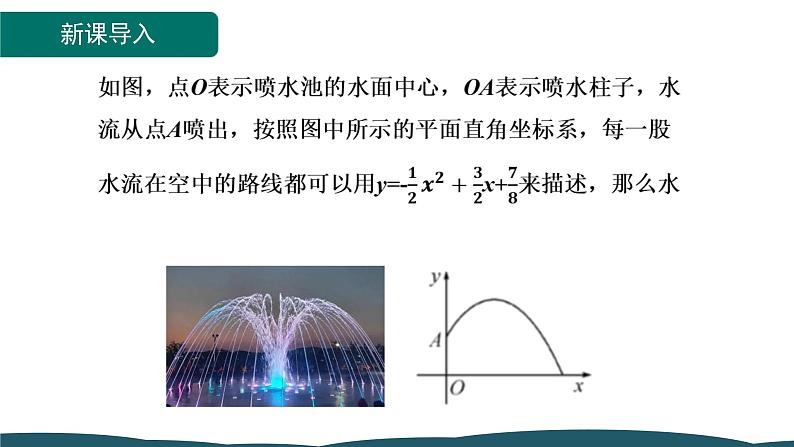
初中数学人教版九年级上册22.2二次函数与一元二次方程课前预习ppt课件

这是一份初中数学人教版九年级上册22.2二次函数与一元二次方程课前预习ppt课件，文件包含222二次函数与一元二次方程pptx、222二次函数与一元二次方程mp4等2份课件配套教学资源，其中PPT共24页， 欢迎下载使用。

回答下列问题：1.一次函数y=x+2的图象与x轴的交点坐标是什么？2.一元一次方程x+2=0的根是多少？3.一次函数y=kx+b的图象与一元一次方程kx+b=0的根有什么关系？
1.请同学们阅读课本43页问题.
②你能根据图象，回答问题（3）（4）吗？
由图象可知，抛物线h=20t-5t2顶点坐标为（2,20），所以小球的飞行高度不可能达到20.5 m.由图象可知，抛物线h=20t-5t2与x轴的公共点为（0,0），（4,0），所以小球从飞出到落地要用4 s.
3.请同学们阅读课本44页思考.4.抛物线与x轴的公共点个数与一元二次方程根的判别式有什么关系?公共点的横坐标与方程的解有什么关系?若b²-4ac>0,则抛物线与x轴有两个公共点；若b²- 4ac=0,则抛物线与x轴有一个公共点；若b²-4ac<0, 则抛物线与x轴没有公共点.公共点的横坐标就是一元二次方程的解.5.请同学们阅读课本46页例题.
1.请同学们归纳二次函数与一元二次方程的联系.抛物线y=ax²+bx+c与x轴的公共点的横坐标为一元二次方程ax²+bx+c=0的根，抛物线y=ax²+bx+c与x 轴的公共点个数与一元二次方程ax²+bx+c=0的根的判别式有关.2.已知抛物线y=2(k+1)x²+4kx+2k-3.(1)当k为何值时，抛物线与x轴有两个公共点?(2)当k为何值时，抛物线与x轴只有一个公共点? (3)当k为何值时，抛物线与x轴没有公共点?
k>-3且k≠-1;k=-3;k<-3
知识点1．二次函数与一元二次方程的联系（难点）二次函数y=ax²+bx+c的图象与x 轴的交点与一元二次方程ax²+bx+c=0的根之间的关系： 二次函数y=ax²+bx+c 的图象与x 轴公共点的横坐标就是一元二次方程ax²+bx+c=0 的 根
注 已知二次函数y=ax2+bx+c的函数值m，求自变量x的值，可以看作解一元二次方程ax2+bx+c=m；反过来，解一元二次方程ax2+bx+c=m，可以看成已知二次函数y=ax2+bx+c的函数值m，求自变量x的值.
知识点2．用图象法求一元二次方程的近似解（重点）利用二次函数图象求一元二次方程的近似解的步骤：（1）作出函数的图象，并由图象确定方程的解的个数。（2）由图象与直线y=0的交点位置确定交点横坐标的范围。（3）观察图象求得方程的解（由于作图或观察存在误差，故由图象求得的解一般是近似的）
知识点3．二次函数与不等式（难点）1.函数值y与某个数值m之间的不等关系，一般要转化成关于x的不等式，解不等式求得自变量x的取值范围。2.利用两个函数图象在直角坐标系中的上下位置关系求自变量的取值范围，可作图利用交点直观求解，也可以利用两个函数解析式列不等式求解。
【题型一】抛物线与坐标轴的公共点问题
（-1,0）和（5,0）
例2: 已知二次函数y=ax2+bx+c，其中y与x的部分对应值如下表：①抛物线的顶点坐标为（1，-9）；②与y轴的交点坐标为（0，-8）；③与x轴的交点坐标为（-2,0）和（2,0）；④当x=-1时，对应的函数值y为-5.以上结论正确的是_________.
【题型二】利用二次函数解一元二次方程
例5:如图，抛物线y=ax²+bx+c 经过点A(0,3),B(2,3),C(-1,0), 直线 y=mx+n 经过点 B,C. (1)该抛物线的对称轴为直线 ___________.(2)关于x的一元二次方程αx²+bx+c=0 的解为 ___________. ( 3 ) 关于x的一元二次方程αx²+bx+c=mx+n的解为___________. (4)若关于 x 的一元二次方程 ax²+bx+c-k=0 无实数根，则 k 的取值范围是___________.
x₁=2,x₂=-1
【题型三】利用二次函数图象求一元二次方程的近似根
例6:已知二次函数 y=ax²+bx+c 的图象如图所示，则一元二次方程ax²+bx+c=0 的近似解为 ( )A. x₁≈-2.1, x₂≈0.1 B. x₁≈-2.5, x₂≈0.5C. x₁≈-2.9, x₂≈0.9 D. x₁≈-3, x₂≈1
例7:已知二次函数y=ax²+bx+c, 其中函数y 与自变量x 的部分对应值如下表，则方程 ax²+bx+c=0 的一个解 x₀ 的取值范围是 ( )
A.0< x₀<0.5 B.0.5< x₀<1 C.1< x₀<1.5 D.1.5< x₀<2
【题型四】利用二次函数的图象解不等式
本节课我们学习了哪些知识？
x ≠ x1的一切实数