广东省汕头市蓝田中学2023-2024学年下学期七年级数学期中核心素养监测卷

这是一份广东省汕头市蓝田中学2023-2024学年下学期七年级数学期中核心素养监测卷，共10页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。
1.下列各图中，∠1与∠2是对顶角的是（ ）

A B C D
2.点 P是由点Q（-3.5）先向下平移3个单位长度，再向右平移5个单位长度而得到的，P点坐标为（ ）A.（-6，10） B.（-2，8） C.（-2，2） D.（2，2）
3.已知是关于x，y的方程，x+ky=3的一个解，则k的值为（ ）
A.-1 B.1 C.2 D.3
4.点P（2，-5）所在的象限是（ ）
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如图，在数轴上表示的点可能是（ ）
A.点P B.点Q C.点M D.点N
6.下列等式成立的是（ ）
A. =±2 B.（－）2=9 C. =6 D. = ±2
7.如图，两条直线相交于点O，若射线OC平分平角∠AOB，∠1=56°，则∠2等于（ ）
A.44° B.56° C.45° D.34°

8.估计的值在哪两个整数之间（ ）
A.75 和 77 B.6 和 7 C.7 和 8 D.8 和 9
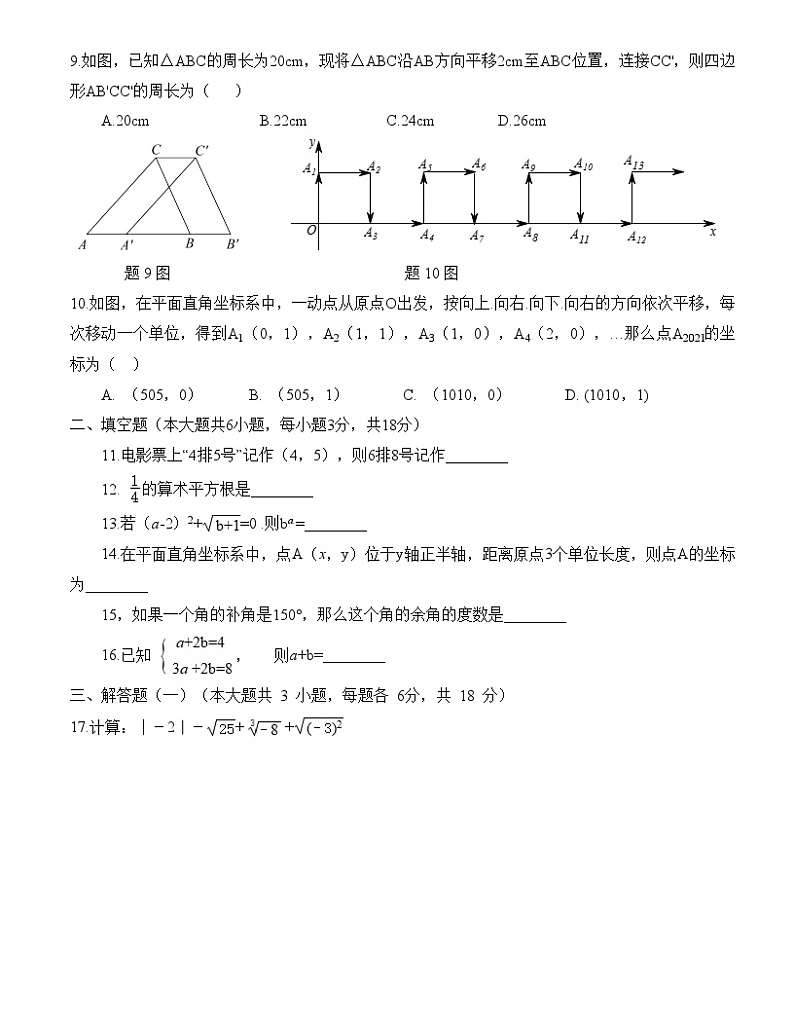
9.如图，已知△ABC的周长为20cm，现将△ABC沿AB方向平移2cm至ABC位置，连接CC'，则四边形AB'CC'的周长为（ ）
A.20cm B.22cm C.24cm D.26cm

题9图 题10图
10.如图，在平面直角坐标系中，一动点从原点O出发，按向上.向右.向下.向右的方向依次平移，每次移动一个单位，得到A1（0，1），A2（1，1），A3（1，0），A4（2，0），…那么点A2021的坐标为（ ）
A. （505，0） B. （505，1） C. （1010，0） D. (1010，1)
二、填空题（本大题共6小题，每小题3分，共18分）
11.电影票上“4排5号”记作（4，5），则6排8号记作________
12. 的算术平方根是________
13.若（a-2）2+=0 .则ba =________
14.在平面直角坐标系中，点A（x，y）位于y轴正半轴，距离原点3个单位长度，则点A的坐标为________
15，如果一个角的补角是150°，那么这个角的余角的度数是________
16.已知 ， 则a+b=________
三、解答题（一）（本大题共 3 小题，每题各 6分，共 18 分）
17.计算：︱－2︱－++
18.解方程组

19.已知：如图，直线a，b被直线c所截，a//b.求证：∠1+∠2=180°.
四、解答题（二）（本大题共4小题，每小题8分，共32分）
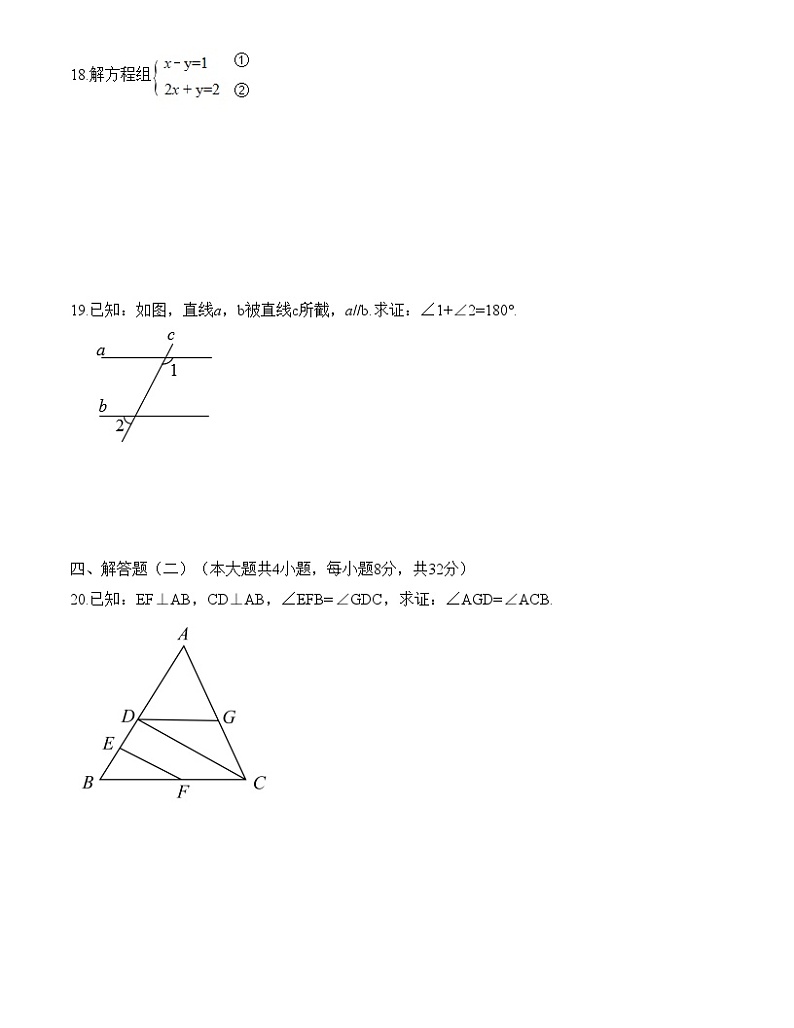
20.已知：EF⊥AB，CD⊥AB，∠EFB=∠GDC，求证：∠AGD=∠ACB.
21.已知5a+2的立方根是3，3a +b-1的算术平方根是4，c是的整数部分
（1）求a，b，c的值：
（2）求3a-b+c的平方根.
22.已知平面直角坐标系中有一点M（2m- 3，m+1）.
（1）点N（5，-1）且 MN//x轴时，求点M的坐标
（2）若点M到y轴的距离为2时，求点M的坐标。
23.如图，已知∠1=∠C，∠2+∠3=180°，试判断∠ADE与∠B的大小关系，并说明理由.
解：∠ADE与∠B的大小关系是_______
证明：∵∠2+∠3=180°（已知）∠3=∠EHG（ ）
∴∠2+∠EHG=180°
∴DG//AC（ ）
∴∠1=∠AED（ ）
∵∠1=∠C
∴∠C=∠AED（ ）
∴______//BC（ ）
∴∠ADE=∠B（ ）

四、解答题（三）（本大题共2小题，24题10分，25题12分，共22分）
24.在平面直角坐标系中，△ABC三个顶点的坐标分别是A（-2，2）、B（2，0），C（-4，-2）.
（1）在平面直角坐标系中画出△ABC：
（2）若将（1）中的△ABC平移，使点B的对应点B'坐标为（6，2），画出平移后的△A'B'C'；
（3）求△A'B'C'的面积.
25.如图 1，在平面直角坐标系中，A（a，0），C（b，2），且满足（a+2）2+ =0，过C作CB⊥x轴于B.
（1）求△ABC的面积.
（2）若过B作BD//AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图2，求∠AED的度数.
（3）在y轴上是否存在点P，使得△ABC和△ACP的面积相等？若存在，求出P点坐标；若不存在，请说明理由
参考答案
一、选择题（本大题共 10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是符合题意要求的
二、填空题（本大题共6小题，每小题3分，共18分）
11. （6，8）
12.
13. 1
14. （0，3）
15. 60°
15. 3
三、解答题（一）（本大题共 3 小题，每题各 6分，共 18 分）
17.解：原式=2－5+（－2）+3
=2－5－2+3
=－2
18.解：用①+②得：3x=3
解得：x=1
用x=1代入②得：
2×1+y=2
解得：y=0
∴方程组的解为
19.证明：如图：
由对顶角相等可得：∠2=∠3
∵a//b
∴∠3+ ∠1=180°（两直线平行同旁内角互补）
∴∠1+ ∠2 = 180°
四、解答题（二）（本大题共4小题，每小题8分，共32分）
20. 证明：∵EF⊥AB，CD⊥AB，EF//CD，
∴∠EFB = ∠DCF，
∵∠EFB = ∠GDC，
∴∠DCF = ∠GDC，
∴DG//BC
∴∠AGD = ∠ACB.
21.解：（1）∵5a+2的立方根是3，
∴5a+2=33，
解得a =5.
∵3a +b-1的算术平方根是4
∴3a +b-1=42.
把a =5代入可得b=2.
∵ c是的整数部分
∴c=3；
∴a =5，b=2，c=3.
（2）解：把：a =5，b=2，c=3代入a -2b+c得：
a -2b+c=4，
∴a -2b+c的平方根是+2.
22.解：（1）∵点N（5，-1）且MN//x轴，
∴m+1=- 1，
∴m=- 2，
∴点M的坐标为（- 7，-1）.
（2）∵点M（2m-3，m+1）到y轴的距离为2.
∴2m-3=2或2m-3=-2
∴m=2.5或m=0.5
∴点M的坐标为（2，3.5）或（- 2，1.5）
23.解：∠ADE与∠B的大小关系是∠ADE= ∠B.
证明：∵∠2+∠3=180°（已知）∠3=∠EHG（对顶角相等）
∴∠2+ ∠EHG=180°
∴DG//AC（同旁内角互补，两直线平行）
∴∠1= ∠AED（两直线平行，内错角相等）
∵∠1= ∠C
∴∠C = ∠ AED（等量代换）
∴DE//BC（同位角相等，两直线平行）
∴∠ADE=∠B（两直线平行，同位角相等）
故答案为：∠ADE=∠B：对顶角相等；同旁内角互补，两直线平行；两直线平行，内错角相等；等量代换；DE；同位角相等，两直线平行；两直线平行，同位角相等
四、解答题（三）（本大题共2小题，24题10分，25题12分，共22分）
24. 解：（1）如图，△ABC为所作；
（2）如图，△A'B'C为所作；
（3）△A'B'C'的面积=6×4－×2×6－×2×4－×4×2=10
25.解：（1）∵（a+2）2+ =0=0
∴a+2=0，b-2=0，
∴a =－2，b=2，
∵CB⊥AB
∴A（－2，0），B（2，0），C（2，2），
∴ΔABC的面积=×2×4=4；
（2）解：∵CB//y轴，BD//AC，
∴∠CAB= ∠5，
又∵∠ODB+ ∠5= 90°
∴∠CAB+ ∠ODB= 90°，
过E作EF//AC，如图①，
∵BD//AC，
∴BD//AC//EF，
∴∠3= ∠1，∠4= ∠2
∵AE，DE分别平分∠CAB，∠ODB，
∴∠3=∠CAB，∠4=∠ODB.
∴∠AED= ∠1+ ∠2=（∠CAB+ ∠ODB）=45°；
（3）存在：
解：①当P在y轴正半轴上时，如图②
设P（0，t），
过P作MN//x轴，AN//y轴，BM//y轴
∴S△APC=S梯形MNAC-S△ANP-S△CMP=4，
∴
解得：t=3
∴P（0，3）
②当P在y轴负半轴上时，如图③
∵S△APC=S梯形MNAC-S△ANP-S△CMP=4
∴
解得：t=－1
∴P（0，－1）
综上所述：P（0，3）或（0，－1）.
1
2
3
4
5
6
7
8
9
10
B
D
B
D
B
C
D
D
C
D