河南省南阳市淅川县2023-2024学年八年级下学期期中数学试题（原卷版+解析版）

这是一份河南省南阳市淅川县2023-2024学年八年级下学期期中数学试题（原卷版+解析版），文件包含河南省南阳市淅川县2023-2024学年八年级下学期期中数学试题原卷版docx、河南省南阳市淅川县2023-2024学年八年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。
2．本试卷上不要答题，请按答题卡上注意事项的要求直接把答案写在答题卡上．答在试题卷上的答案无效．
一、选择题（本大题共10小题，每小题3分，共30分）
1. 若分式有意义，则x应满足的条件是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题主要考查分式有意义的条件：分母不能为0
【详解】解：∵x-2≠0，
∴x≠2，
故选A．
【点睛】本题考查的是分式有意义的条件，当分母不为0时，分式有意义．
2. 下列计算正确的是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】此题考查分式的基本性质，分式的混合运算，关键是根据把分式的分子和分母扩大还是缩小相同的倍数，分式的值不变解答．分子和分母同乘以（或除以）一个不为0的数，分数值不变．
【详解】解：A、，错误；
B、，错误；
C、，错误；
D、，正确；
故选：D
3. 已知正比例函数的图象如图所示经过点(3，－3)，则这个函数的关系式为（ ）

A. y＝xB. y＝－xC. y＝－3xD. y＝3x
【答案】B
【解析】
【分析】首先根据图象是经过原点的直线可得此函数是正比例函数，所以设解析式为y=kx（k≠0），把图象所经过的点（3，-3）代入设出的函数解析式，计算出k的值，进而得到函数解析式．
【详解】设函数解析式为y=kx（k≠0），
∵图象经过（3，-3），∴-3=k×3，解得k=-1，
∴这个函数的关系式为y=-x，故选：B．
【点睛】此题主要考查了待定系数法求函数解析式，关键是掌握凡是图象经过的点必能满足解析式
4. 2023年9月，华为最新的发售，销量遥遥领先，其中使用的华为新麒麟芯片突破5纳米（1纳米毫米）制程工艺，数据“5纳米”用科学记数法表示为（ ）
A. 毫米B. 毫米C. 毫米D. 毫米
【答案】C
【解析】
【分析】本题考查了科学记数法；“将一个数表示成的形式，其中，为整数，这种记数的方法叫做科学记数法”，熟记科学记数法的定义是解题关键．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．根据科学记数法的定义即可得．
【详解】解：5纳米毫米．
故选：C．
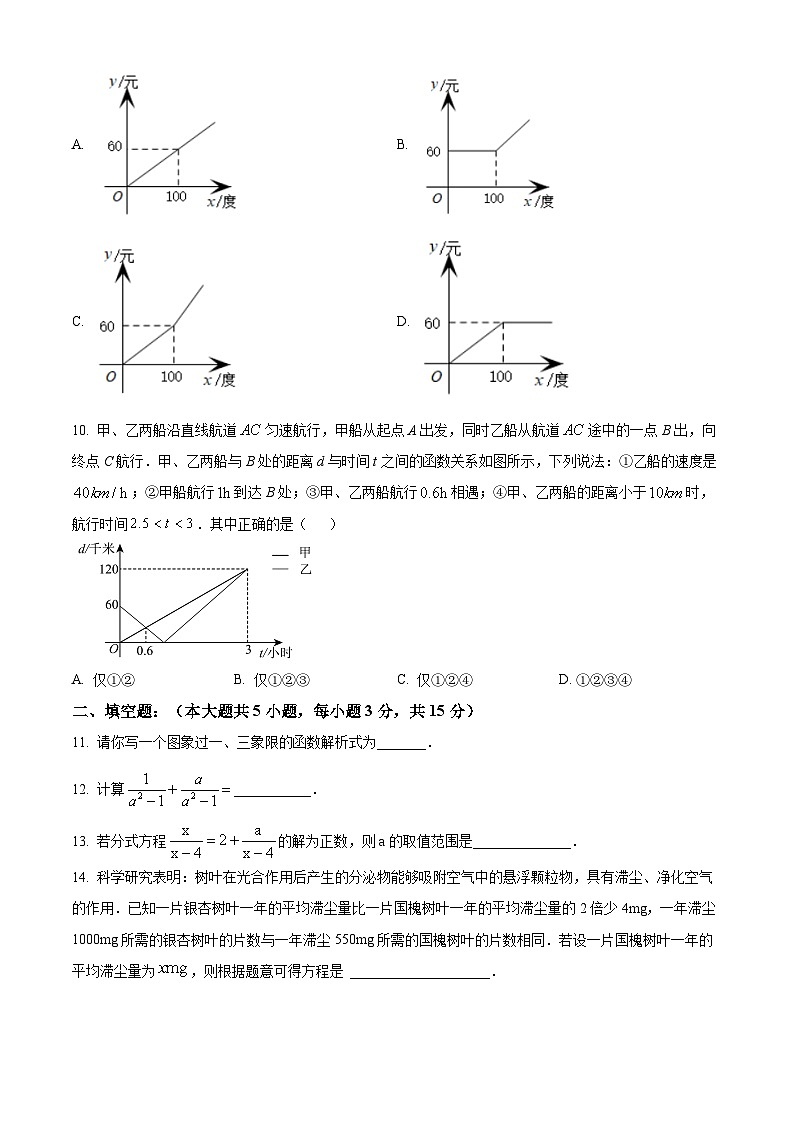
5. 下列函数图像中，能反映等腰三角形顶角（度）与底角（度）之间函数关系的是（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】等腰三角形的两个底角相等，由内角和定理可知：x+x+y=180，进而可得，y=180-2x，由y＞0得：x＜90，又x＞0，故0＜x＜90．
【详解】∵等腰三角形的两个底角相等，
∴y+2x=180°，
∴y=-2x+180°，
∵-20，
∴图象经过一、二、四象限，
∵y>0，x>0，
∴0y2，因此该单位选择乙厂更节省费用．
（求出当x=8时，y1和y2的值，用比较大小的方法得到结论也正确）
考点：一次函数的应用．
22. 某快递公司为了提高工作效率，计划购买A，B两种型号的机器人来搬运货物，已知每台A型机器人比每台B型机器人每天多搬运20吨，并且3台A型机器人和2台B型机器人每天共搬运货物460吨．
（1）求每台A型机器人和每台B型机器人每天分别搬运货物多少吨?
（2）每台A型机器人售价3万元，每台B型机器人售价2万元，该公司计划采购A，B两种型号的机器人共20台，必须满足每天搬运的货物不低于1800吨，该公司应该如何设计采购方案才能使得费用最低，最低费用是多少?
【答案】（1）100吨，80吨
（2）A种型号的机器人采购10台，B种型号的机器人采购10台时费用最低为50万元
【解析】
【分析】考查了二元一次方程组的应用及一次函数应用．解决问题的关键是读懂题意，找到关键描述语，找到所求的量的等量关系．列出对应的方程组，极值问题来利用函数的递增情况解决
（1）题目中的等量关系是：①每台型机器人比每台型机器人每天多搬运20吨，②3台型机器人和2台型机器人每天共搬运货物460吨．
（2）题目中的不等关系是：每天搬运的货物不低于1800吨，等量关系是：总费用型机器费用型机器费用，极值问题来利用函数的递增情况解决．
【小问1详解】
设每台型机器人每天搬运货物吨，每台型机器人每天搬运货物吨，
，
解得，
每台型机器人每天搬运货物100吨，每台型机器人每天搬运货物80吨；
【小问2详解】
设种机器人采购台，种机器人采购台，总费用为（万元），
．
解得：．
．
，
随着的减少而减少．
当时，有最小值，．
、两种机器人分别采购10台，10台时，所需费用最低，最低费用是50万元．
23. 我们把形如（，不为零），且两个解分别为，的方程称为“十字分式方程”．例如为十字分式方程，可化为，所以，．再如为十字分式方程，可化为，所以，．
应用上面的结论解答下列问题：
（1）若为十字分式方程，则 ， ；
（2）若十字分式方程的两个解分别为，，求的值；
（3）设为常数且，若关于的十字分式方程的两个解分别为，，求的值．
【答案】（1），
（2）
（3）4
【解析】
【分析】本题考查根与系数的关系，分式方程；理解“阅读材料”中的答题方法，能够将所求分式方程转化为求解是解题的关键．
（1）类比题目中“阅读材料”的答题方法即可求解．
（2）结合运用“阅读材料”即可求出和的值，并代数运算即可求解；
（3）善于观察并分析方程，即可求出和的值，代入运算即可求解．
【小问1详解】
解：可化，
，
经检验是该方程的解．
【小问2详解】
∵的两个解分别为，，
故，
．
【小问3详解】
原方程变为，
，
，
，
．