广东省深圳市福田区实验教育集团侨香学校2023-2024学年七年级下学期期中考试数学试卷

这是一份广东省深圳市福田区实验教育集团侨香学校2023-2024学年七年级下学期期中考试数学试卷，共18页。

A．x6÷x3＝x2B．a3•a2＝a5
C．（2x）3＝6x3D．5a3﹣4a2＝a2
2．（3分）澳大利亚昆士兰大学的科学家在海底下约4.8公里深处的沙岩中，发现了一种世界上最小的神秘生物，它们的最大身长只有0.00000015米，甚至比已知的最小细菌还要小，将0.00000015用科学记数法表示为（ ）
A．0.15×10﹣6B．1.5×10﹣7C．1.5×10﹣8D．15×10﹣9
3．（3分）下列作图能表示点A到BC的距离的是（ ）
A．B．
C．D．
4．（3分）下列计算结果正确的是（ ）
A．（x+y）2＝x2+y2
B．（x﹣y）2＝x2﹣2xy﹣y2
C．（x+2y）（x﹣2y）＝x2﹣2y2
D．（3x+y）2＝9x2+6xy+y2
5．（3分）已知2m＝3，2n＝4，则23m﹣2n的值为（ ）
A．B．C．D．1
6．（3分）某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据（如下表）：
下列说法错误的是（ ）
A．在这个变化中，自变量是温度，因变量是声速
B．温度越高，声速越快
C．当空气温度为20℃时，声速为342m/s
D．当温度每升高10℃，声速增加8m/s
7．（3分）小华同学喜欢锻炼，周六他先从家跑步到新华公园，在那里与同学打一会儿羽毛球后又步行回家，下面能反映小华离家距离y与所用时间x之间关系的图象是（ ）
A．B．
C．D．
8．（3分）下列说法正确的个数是（ ）
①两直线平行，同旁内角相等；
②过一点有且只有一条直线与已知直线平行；
③若一个角的两边分别与另一个角的两边平行，则这两个角相等；
④平行于同一条直线的两条直线平行．
A．1个B．2个C．3个D．4个
9．（3分）如图，AB∥CD∥EF，则下列各式中正确的是（ ）
A．∠1＝180°﹣∠3B．∠1＝∠3﹣∠2
C．∠2+∠3＝180°﹣∠1D．∠2+∠3＝180°+∠1
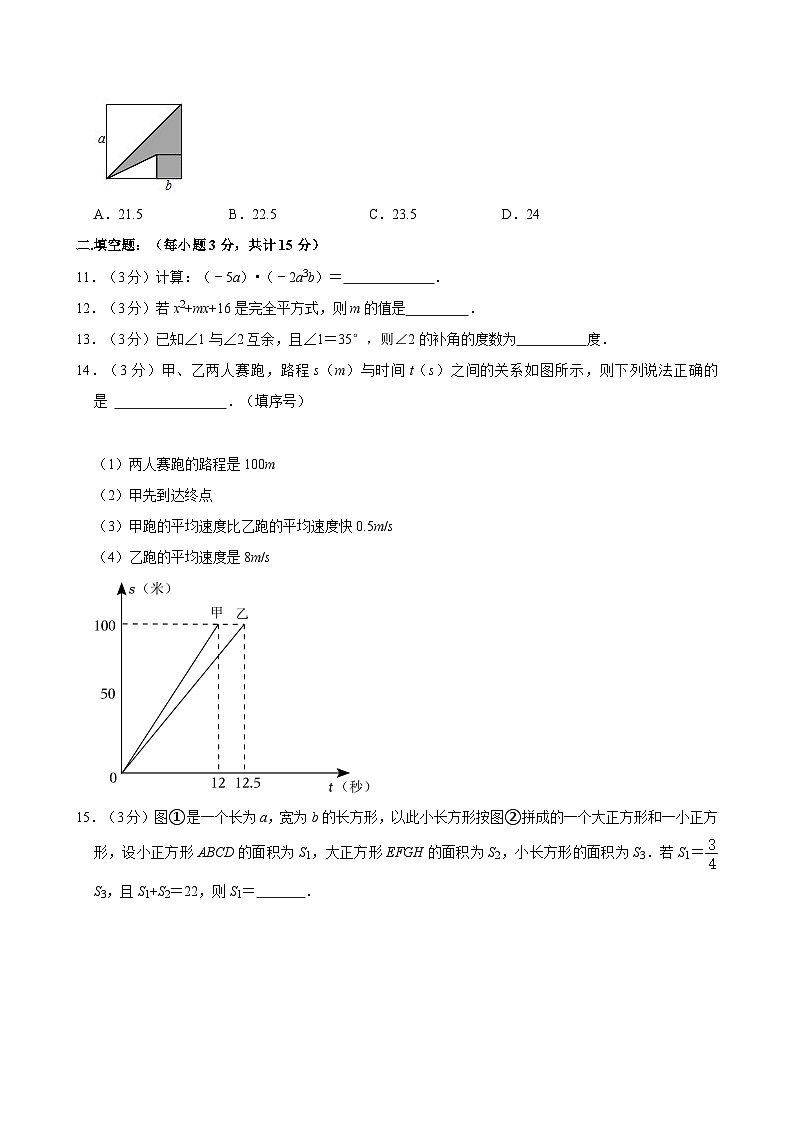
10．（3分）如图，两个正方形边长分别为a，b，如果a+b＝9，ab＝12，则阴影部分的面积为（ ）
A．21.5B．22.5C．23.5D．24
二.填空题：（每小题3分，共计15分）
11．（3分）计算：（﹣5a）•（﹣2a3b）＝ ．
12．（3分）若x2+mx+16是完全平方式，则m的值是 ．
13．（3分）已知∠1与∠2互余，且∠1＝35°，则∠2的补角的度数为 度．
14．（3分）甲、乙两人赛跑，路程s（m）与时间t（s）之间的关系如图所示，则下列说法正确的是 ．（填序号）
（1）两人赛跑的路程是100m
（2）甲先到达终点
（3）甲跑的平均速度比乙跑的平均速度快0.5m/s
（4）乙跑的平均速度是8m/s
15．（3分）图①是一个长为a，宽为b的长方形，以此小长方形按图②拼成的一个大正方形和一小正方形，设小正方形ABCD的面积为S1，大正方形EFGH的面积为S2，小长方形的面积为S3．若S1＝S3，且S1+S2＝22，则S1＝ ．
三.解答题：（共7小题，其中第16题12分，第17题5分，第18题7分，第19题6分，第20题8分，第21题7分.第22题10分，共55分）
16．（12分）计算：
（1）；
（2）（﹣3a4）2﹣a•a3•a4﹣a10÷a2；
（3）20232﹣2022×2024．
17．（5分）先化简，后求值：[（2a﹣b）2﹣（b+2a）（b﹣2a）]÷（4a），其中．
18．（7分）填空：（请补全下列证明过程及括号内的推理依据）
已知：如图，∠1＝∠2，∠C＝∠D，求证：∠A＝∠F．
证明：∵∠1＝∠2（已知），
∠1＝∠3（ ），
∴∠2＝∠3（等量代换）．
∴BD∥CE（ ）．
∴∠D＝∠ （ ）．
又∵∠C＝∠D（已知），
∴∠C＝∠ （等量代换）．
∴ ∥ （ ）．
∴∠A＝∠F（ ）．
19．（6分）如图，已知直线AB和CD相交于O点，∠DOE是直角，OF平分∠AOE，∠BOD＝22°，求∠AOE和∠COF的度数．
20．（8分）小明晚饭后外出散步，碰见同学，交谈一会，返回途中在读报栏看了一会报．如图是根据此情景画出的图象，请你回答下列问题：
（1）小明碰见同学后交谈了 分钟．
（2）读报栏离家 米．
（3）小明出发15分钟后离家 米．
（4）小明出发 分钟后离家500米．
21．（7分）从边长为a的正方形中减掉一个边长为b的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．
（1）上述操作能验证的等式是 ；
（2）运用你从（1）写出的等式，完成下列各题：
①已知：a﹣b＝3，a2﹣b2＝21，求a+b的值；
②计算：．
22．（10分）问题探究：
如图①，已知AB∥CD，我们发现∠E＝∠B+∠D．我们怎么证明这个结论呢？
张山同学：如图②，过点E作EF∥AB，把∠BED分成∠BEF与∠DEF的和，然后分别证明∠BEF＝∠B，∠DEF＝∠D．
李思同学：如图③，过点B作BF∥DE，则∠E＝∠EBF，再证明∠ABF＝∠D．
问题解答：
（1）请按张山同学的思路，写出证明过程；
（2）请按李思同学的思路，写出证明过程；
问题迁移：
（3）如图④，已知AB∥CD，EF平分∠AEC，FD平分∠EDC．若∠CED＝3∠F，请直接写出∠F的度数．
参考答案与试题解析
一.单项选择题：（每小题只有一个选项符合题意，每小题3分，共计30分）
1．（3分）下列运算正确的是（ ）
A．x6÷x3＝x2B．a3•a2＝a5
C．（2x）3＝6x3D．5a3﹣4a2＝a2
【解答】解：A．x6÷x3＝x3，故此选项不合题意；
B．a3•a2＝a5，故此选项符合题意；
C．（2x）3＝8x3，故此选项不合题意；
D．5a3﹣4a2，无法合并，故此选项不合题意．
故选：B．
2．（3分）澳大利亚昆士兰大学的科学家在海底下约4.8公里深处的沙岩中，发现了一种世界上最小的神秘生物，它们的最大身长只有0.00000015米，甚至比已知的最小细菌还要小，将0.00000015用科学记数法表示为（ ）
A．0.15×10﹣6B．1.5×10﹣7C．1.5×10﹣8D．15×10﹣9
【解答】解：0.00000015＝1.5×10﹣7．
故选：B．
3．（3分）下列作图能表示点A到BC的距离的是（ ）
A．B．
C．D．
【解答】解：A、BD表示点B到AC的距离，故此选项错误；
B、AD表示点A到BC的距离，故此选项正确；
C、AD表示点D到AB的距离，故此选项错误；
D、CD表示点C到AB的距离，故此选项错误；
故选：B．
4．（3分）下列计算结果正确的是（ ）
A．（x+y）2＝x2+y2
B．（x﹣y）2＝x2﹣2xy﹣y2
C．（x+2y）（x﹣2y）＝x2﹣2y2
D．（3x+y）2＝9x2+6xy+y2
【解答】解：A、原式＝x2+y2+2xy，错误；
B、原式＝x2﹣2xy+y2，错误；
C、原式＝x2﹣4y2，错误；
D、原式＝9x2+6xy+y2，正确，
故选：D．
5．（3分）已知2m＝3，2n＝4，则23m﹣2n的值为（ ）
A．B．C．D．1
【解答】解：∵2m＝3，2n＝4，
∴23m﹣2n＝23m÷22n＝（2m）3÷（2n）2＝33÷42＝．
故选：B．
6．（3分）某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据（如下表）：
下列说法错误的是（ ）
A．在这个变化中，自变量是温度，因变量是声速
B．温度越高，声速越快
C．当空气温度为20℃时，声速为342m/s
D．当温度每升高10℃，声速增加8m/s
【解答】解：∵在这个变化中，自变量是温度，因变量是声速，
∴选项A说法正确，不符合题意；
∵根据数据表，可得温度越低，声速越慢，温度越高，声速越快，
∴选项B说法正确，不符合题意；
由列表可知，当空气温度为20℃时，声速为342m/s，
∴选项C说法正确，不符合题意；
∵324﹣318＝6（m/s），330﹣324＝6（m/s），336﹣330＝6（m/s），342﹣336＝6（m/s），348﹣342＝6（m/s），
∴当温度每升高10℃，声速增加6m/s，
∴选项D说法不正确，符合题意；
故选：D．
7．（3分）小华同学喜欢锻炼，周六他先从家跑步到新华公园，在那里与同学打一会儿羽毛球后又步行回家，下面能反映小华离家距离y与所用时间x之间关系的图象是（ ）
A．B．
C．D．
【解答】解：∵小华从家跑步到离家较远的新华公园，
∴随着时间的增加离家的距离越来越远，
∵他在那里与同学打一段时间的羽毛球，
∴他离家的距离不变，
又∵再步行回家，
∴他离家越来越近，
∴小华同学离家的距离y与所用时间x之间函数图象的大致图象是B．
故选：B．
8．（3分）下列说法正确的个数是（ ）
①两直线平行，同旁内角相等；
②过一点有且只有一条直线与已知直线平行；
③若一个角的两边分别与另一个角的两边平行，则这两个角相等；
④平行于同一条直线的两条直线平行．
A．1个B．2个C．3个D．4个
【解答】解：①两直线平行，同旁内角互补；故错误；
②过直线外一点有且只有一条直线与已知直线平行；故正确；
③若一个角的两边分别与另一个角的两边平行，则这两个角相等或互补；故错误；
④平行于同一条直线的两条直线平行；故正确；
所以正确的个数是2个．
故选：B．
9．（3分）如图，AB∥CD∥EF，则下列各式中正确的是（ ）
A．∠1＝180°﹣∠3B．∠1＝∠3﹣∠2
C．∠2+∠3＝180°﹣∠1D．∠2+∠3＝180°+∠1
【解答】解：∵AB∥CD，
∴∠2+∠BDC＝180°，即∠BDC＝180°﹣∠2，
∵EF∥CD，
∴∠BDC+∠1＝∠3，即∠BDC＝∠3﹣∠1，
∴180°﹣∠2＝∠3﹣∠1，即∠2+∠3＝180°+∠1，
故选：D．
10．（3分）如图，两个正方形边长分别为a，b，如果a+b＝9，ab＝12，则阴影部分的面积为（ ）
A．21.5B．22.5C．23.5D．24
【解答】解：根据题意，得
∵a+b＝9，ab＝12，
∴（a+b）2＝92
∴a2+2ab+b2＝81，
∴a2+b2＝81﹣24＝57，
∴阴影部分的面积为：
a2﹣b（a﹣b）
＝（a2﹣ab+b2）
＝（57﹣12）
＝22.5．
故选：B．
二.填空题：（每小题3分，共计15分）
11．（3分）计算：（﹣5a）•（﹣2a3b）＝ 10a4b． ．
【解答】解：（﹣5a）•（﹣2a3b）＝10a4b．
故答案为：10a4b．
12．（3分）若x2+mx+16是完全平方式，则m的值是 ±8 ．
【解答】解：∵x2+mx+16是一个完全平方式，
∴x2+mx+16＝（x±4）2，
＝x2±8x+16．
∴m＝±8，
故答案为：±8．
13．（3分）已知∠1与∠2互余，且∠1＝35°，则∠2的补角的度数为 125 度．
【解答】解：∠1与∠2互余，且∠1＝35°，
则∠2＝90°﹣35°＝55°，
∠2的补角的度数为180°﹣55°＝125°．
故填125．
14．（3分）甲、乙两人赛跑，路程s（m）与时间t（s）之间的关系如图所示，则下列说法正确的是 （1）（2）（4） ．（填序号）
（1）两人赛跑的路程是100m
（2）甲先到达终点
（3）甲跑的平均速度比乙跑的平均速度快0.5m/s
（4）乙跑的平均速度是8m/s
【解答】解：（1）两人赛跑的路程是100m，故（1）正确；
（2）甲先到达终点，故（2）正确；
（3）甲跑的平均速度为m/s，乙跑的平均速度为m/s，
甲跑的平均速度比乙跑的平均速度快m/s，故（3）不正确，
（4）乙跑的平均速度是8m/s，正确．
故答案为：（1）（2）（4）．
15．（3分）图①是一个长为a，宽为b的长方形，以此小长方形按图②拼成的一个大正方形和一小正方形，设小正方形ABCD的面积为S1，大正方形EFGH的面积为S2，小长方形的面积为S3．若S1＝S3，且S1+S2＝22，则S1＝ 3 ．
【解答】解：由图可得：大正方形EFGH的面积＝小正方形ABCD的面积+4×小长方形的面积，即S2＝S1+4S3，
∵S1＝S3，
∴S3＝S1，
∵S1+S2＝22，
∴S2＝22﹣S1，
∴22﹣S1＝S1+4×S1，
解得S1＝3．
故答案为：3．
三.解答题：（共7小题，其中第16题12分，第17题5分，第18题7分，第19题6分，第20题8分，第21题7分.第22题10分，共55分）
16．（12分）计算：
（1）；
（2）（﹣3a4）2﹣a•a3•a4﹣a10÷a2；
（3）20232﹣2022×2024．
【解答】解：（1）原式＝9+2+1
＝12；
（2）原式＝9a8﹣a8﹣a8
＝7a8；
（3）原式＝20232﹣（2023﹣1）×（2023+1）
＝20232﹣20232+1
＝1．
17．（5分）先化简，后求值：[（2a﹣b）2﹣（b+2a）（b﹣2a）]÷（4a），其中．
【解答】解：原式＝[4a2﹣4ab+b2﹣（b2﹣4a2）]÷（4a）
＝（4a2﹣4ab+b2﹣b2+4a2）÷（4a）
＝（8a2﹣4ab）÷（4a）
＝2a﹣b，
当时，原式＝．
18．（7分）填空：（请补全下列证明过程及括号内的推理依据）
已知：如图，∠1＝∠2，∠C＝∠D，求证：∠A＝∠F．
证明：∵∠1＝∠2（已知），
∠1＝∠3（ 对顶角相等 ），
∴∠2＝∠3（等量代换）．
∴BD∥CE（ 同位角相等，两直线平行 ）．
∴∠D＝∠ 4 （ 两直线平行，同位角相等 ）．
又∵∠C＝∠D（已知），
∴∠C＝∠ 4 （等量代换）．
∴ DF ∥ AC （ 内错角相等，两直线平行 ）．
∴∠A＝∠F（ 两直线平行，内错角相等 ）．
【解答】证明：∵∠1＝∠2 （已知），
∠1＝∠3（对顶角相等），
∴∠2＝∠3（等量代换），
∴BD∥CE（同位角相等，两直线平行），
∴∠D＝∠4 （ 两直线平行，同位角相等），
又∵∠C＝∠D（已知），
∴∠C＝∠4（等量代换），
∴DF∥AC（内错角相等，两直线平行），
∴∠A＝∠F（两直线平行，内错角相等）．
故答案为：对顶角相等；同位角相等，两直线平行；4；两直线平行，同位角相等；4；DF；AC；内错角相等，两直线平行；两直线平行，内错角相等．
19．（6分）如图，已知直线AB和CD相交于O点，∠DOE是直角，OF平分∠AOE，∠BOD＝22°，求∠AOE和∠COF的度数．
【解答】解：∵∠DOE是直角，
∴∠COE＝180°﹣90°＝90°，
又∠AOC＝∠BOD＝22°，
∴∠AOE＝∠AOC+∠COE＝112°，
又OF平分∠AOE，
∴∠AOF＝∠AOE＝56°，
∴∠COF＝∠AOF﹣∠AOC＝56°﹣22°＝34°．
20．（8分）小明晚饭后外出散步，碰见同学，交谈一会，返回途中在读报栏看了一会报．如图是根据此情景画出的图象，请你回答下列问题：
（1）小明碰见同学后交谈了 10 分钟．
（2）读报栏离家 400 米．
（3）小明出发15分钟后离家 600 米．
（4）小明出发 12.5或37.5 分钟后离家500米．
【解答】解：（1）30﹣20＝10（分钟），
∴小明碰见同学后交谈了10分钟．
故答案为：10．
（2）根据图象可知，读报栏离家400米．
故答案为：400．
（3）当0≤t≤20时，小明的速度为800÷20＝40（米/分），
则小明出发15分钟后离家的距离为40×15＝600（米）．
故答案为：600．
（4）当0≤t≤20时，y与t的关系式为y＝40x，
当40x＝500时，解得x＝12.5；
当30≤t≤40时，设y与t的关系式为y＝kx+b（k、b为常数，且k≠0）．
将坐标（30，800）和（40，400）代入y＝kx+b，
得，
解得，
∴y与t的关系式为y＝﹣40t+2000，
当﹣40t+2000＝500时，解得t＝37.5．
综上，小明出发12.5或37.5分钟后离家500米．
故答案为：12.5或37.5
21．（7分）从边长为a的正方形中减掉一个边长为b的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．
（1）上述操作能验证的等式是 a2﹣b2＝（a+b）（a﹣b）． ；
（2）运用你从（1）写出的等式，完成下列各题：
①已知：a﹣b＝3，a2﹣b2＝21，求a+b的值；
②计算：．
【解答】解：（1））∵从边长为a的正方形中减掉一个边长为b的正方形（如图1），然后将剩余部分拼成一个长方形（如图2），
∴图1剩余部分的面积为a2﹣b2，图2的面积为（a+b）（a﹣b），二者相等，从而能验证的等式为：a2﹣b2＝（a+b）（a﹣b）．
故答案为：a2﹣b2＝（a+b）（a﹣b）．
（2）①∵a﹣b＝3，a2﹣b2＝21，a2﹣b2＝（a+b）（a﹣b），
∴21＝（a+b）×3，
∴a+b＝7；
②原式＝
＝ x
＝
＝．
22．（10分）问题探究：
如图①，已知AB∥CD，我们发现∠E＝∠B+∠D．我们怎么证明这个结论呢？
张山同学：如图②，过点E作EF∥AB，把∠BED分成∠BEF与∠DEF的和，然后分别证明∠BEF＝∠B，∠DEF＝∠D．
李思同学：如图③，过点B作BF∥DE，则∠E＝∠EBF，再证明∠ABF＝∠D．
问题解答：
（1）请按张山同学的思路，写出证明过程；
（2）请按李思同学的思路，写出证明过程；
问题迁移：
（3）如图④，已知AB∥CD，EF平分∠AEC，FD平分∠EDC．若∠CED＝3∠F，请直接写出∠F的度数．
【解答】解：（1）如图②中，过点E作EF∥AB，
∵AB∥CD，EF∥AB，
∴AB∥EF∥CD，
∴∠B＝∠BEF，∠D＝∠DEF，
∴∠BED＝∠BEF+∠DEF＝∠B+∠D．
（2）如图③中，过点B作BF∥DE交CD的延长线于G．
∵DE∥FG，
∴∠EDC＝∠G，∠DEB＝∠EBF，
∵AB∥CG，
∴∠G＝∠ABF，
∴∠EDC＝∠ABF，
∴∠DEB＝∠EBF＝∠ABE+∠ABF＝∠ABE+∠EDC．
（3）如图④中，
∵EF平分∠AEC，FD平分∠EDC，
∴∠AEF＝∠CEF，∠CDF＝∠EDF，
设∠AEF＝∠CEF＝x，∠CDF＝∠EDF＝y，则∠F＝x+y，
∵∠CED＝3∠F，
∴∠CED＝3x+3y，
∵AB∥CD，
∴∠BED＝∠CDE＝2y，
∵∠AEC+∠CED+∠DEB＝180°，
∴5x+5y＝180°，
∴x+y＝36°，
∴∠F＝36°．
温度/℃
﹣20
﹣10
0
10
20
30
声速/（m/s）
318
324
330
336
342
348
温度/℃
﹣20
﹣10
0
10
20
30
声速/（m/s）
318
324
330
336
342
348