2024年中考数学押题密卷 广州市专用03

这是一份2024年中考数学押题密卷 广州市专用03，共26页。

注意事项:
1．答题前，考生务必在答题卡第1面、第3面、第5面上用黑色字迹的钢笔或签字笔填写自己的考生号、姓名；将自己的条形码粘贴在答题卡的“条形码粘贴处”。
2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。答案不能答在试卷上。
3．非选择题答案必须用黑色字迹的钢笔或签字笔写在答题卡各题目指定区域内的相应位置上，涉及作图的题目，用2B铅笔画图；如需改动，先划掉原来的答案，然后再写上新的答案，改动后的答案也不能超出指定的区域；不准使用铅笔（作图除外）、涂改液和修正带。不按以上要求作答的答案无效。
4．考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回。
第一部分 选择题（共30分）
一、选择题（本大题共10小题，每小题3分，满分30分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．（3分）（2024•崂山区一模）的倒数是
A．B．5C．D．
2．（3分）（2024•西峰区校级一模）某种生物细胞的直径约为，将0.000506用科学记数法表示为
A．B．C．D．
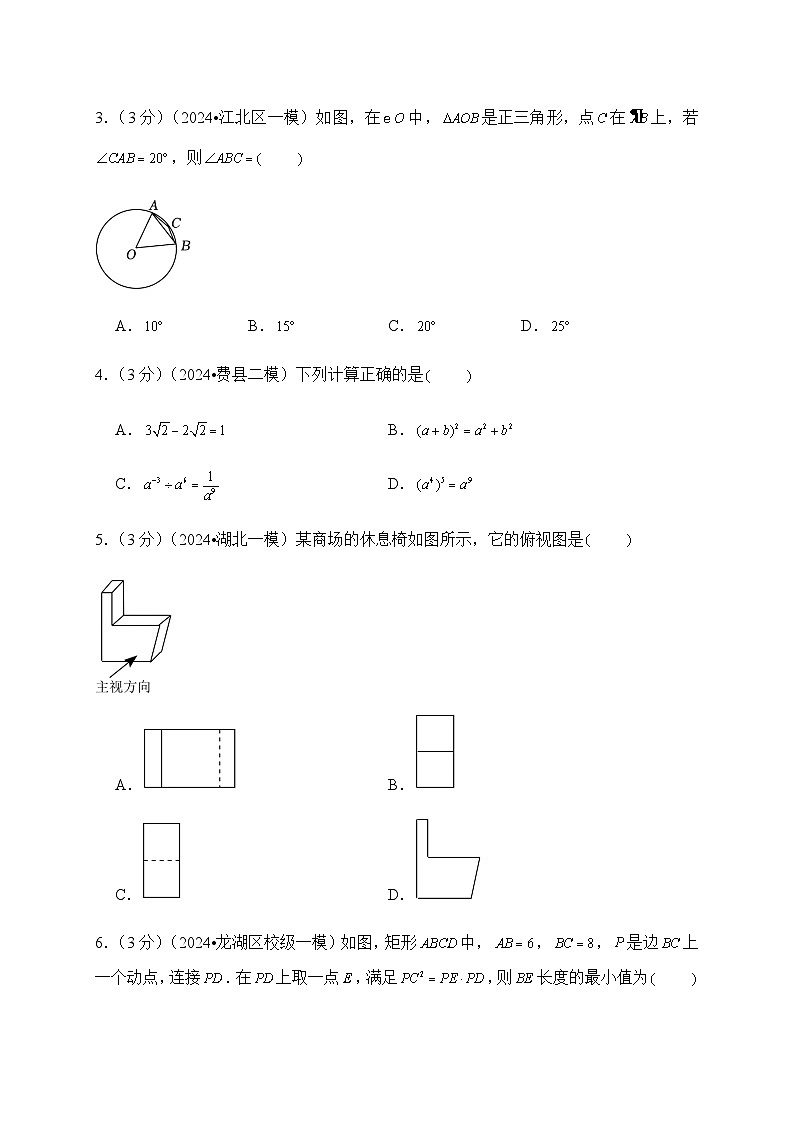
3．（3分）（2024•江北区一模）如图，在中，是正三角形，点在上，若，则
A．B．C．D．
4．（3分）（2024•费县二模）下列计算正确的是
A．B．
C．D．
5．（3分）（2024•湖北一模）某商场的休息椅如图所示，它的俯视图是
A．B．
C．D．
6．（3分）（2024•龙湖区校级一模）如图，矩形中，，，是边上一个动点，连接．在上取一点，满足，则长度的最小值为
A．6.4B．C．D．2
7．（3分）（2024•深圳模拟）如图，在中，，，以点为圆心，以为半径作弧交于点，再分别以，为圆心，以大于长为半径作弧，两弧相交于点，作射线交于点，连接．以下结论不正确的是
A．B．C．D．
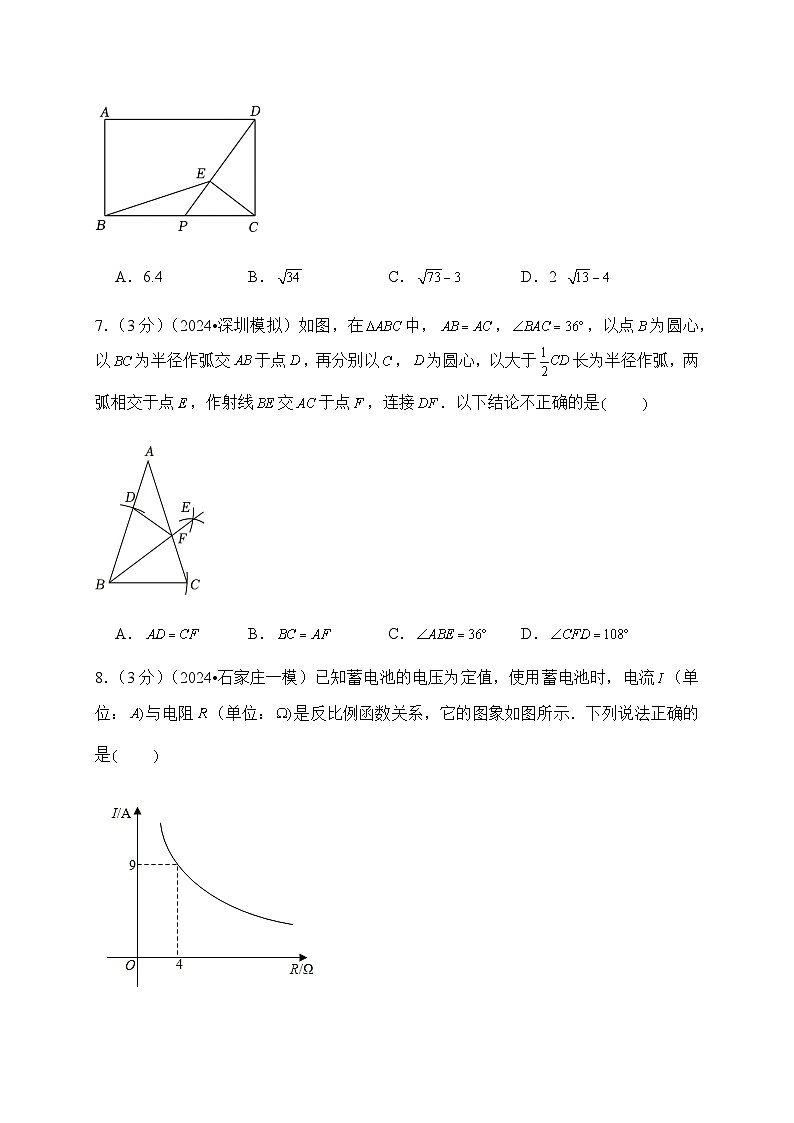
8．（3分）（2024•石家庄一模）已知蓄电池的电压为定值，使用蓄电池时，电流（单位：与电阻（单位：是反比例函数关系，它的图象如图所示．下列说法正确的是
A．函数解析式为B．蓄电池的电压是
C．当时，D．当时，
9．（3分）（2024•崂山区一模）已知二次函数的图象与轴的一个交点坐标为，对称轴为直线，下列结论中：①；②若点，，均在该二次函数图象上，则；③方程的两个实数根为，，且，则，；④若为任意实数，则．正确结论的序号为
A．①②④B．①③④C．②③④D．①③
10．（3分）（2024•费县二模）如图1，在中，点为的中点，动点从点出发，沿着的路径以每秒1个单位长度的速度运动到点，在此过程中线段的长度随着运动时间的函数关系如图2所示，则的长为
A．B．C．D．
第二部分 非选择题（共90分）
二、填空题（本大题共6小题，每小题3分，满分18分．）
11．（3分）（2024•恩施市校级一模）当 时，分式的值为零．
12．（3分）（2024•青白江区模拟）反比例函数的图象在每一象限内，的值随值的增大而减小，那么的取值范围是 ．
13．（3分）（2024•北京模拟）因式分解 ．
14．（3分）（2024•西吉县一模）网络是第五代移动通信网络，它将推动我国数字经济发展迈上新台阶．据预测，2020年到2030年中国直接经济产出和间接经济产出的情况如图所示．
根据如图提供的信息，下列推断合理的是 ．
①2030年间接经济产出比直接经济产出多4.2万亿元；
②2020年到2030年，直接经济产出和间接经济产出都是逐年增长；
③2030年直接经济产出约为2020年直接经济产出的13倍；
④2022年到2023年与2023年到2024年间接经济产出的增长率相同．
15．（3分）（2024•北京一模）如图，是的弦，且，点是弧中点，点是优弧上的一点，，则圆心到弦的距离等于 ．
16．（3分）（2024•丰台区一模）如图，是的中位线，点在上，，连接并延长，与的延长线交于点．若，则线段的长为 ．
三、解答题（本大题共9小题，满分72分．解答应写出文字说明、证明过程或演算步骤．）
17．（4分）（2024•马鞍山一模）解方程：．
18．（4分）（2023•横山区三模）如图，线段，相交于点，且，点，在线段上，．求证：．
19．（6分）（2024•增城区一模）已知．
（1）化简；
（2）若，是方程的两个根，求的值．
20．（6分）（2024•拱墅区模拟）某校随机抽取50位学生测试劳动素养，并将测试结果分别绘制成如图所示的扇形统计图和未完成的频数分布直方图（每组不含前一个边界值，含后一个边界值）．已知测试综合得分大于70分的学生劳动素养为优良．
（1）补全频数分布直方图．
（2）该校共有1000名学生，估计劳动素养为优良的人数．
21．（8分）（2024•湖南模拟）已知是的直径，点是延长线上一点，，是的弦，．
（1）求证：直线是的切线；
（2）若，垂足为，的半径为10，求的长．
22．（10分）（2024•西吉县一模）已知某品牌电动车电池的电压为定值，某校物理小组的同学发现使用该电池时，电流（单位：与电阻（单位：是反比例函数关系，它的图象如图所示．
（1）求该品牌电动车电池的电压；
（2）该物理小组通过询问经销商得知该电动车以最高速度行驶时，工作电压为电池的电压，工作电流在的范围，请你帮该小组确定这时电阻值的范围．
23．（10分）（2024•山亭区一模）为拓展学生视野，某校组织师生开展研学活动，原计划租用甲种客车若干辆，但有15人没有座位；若租用同样数量的乙种客车，则多出三辆车，且其余客车恰好坐满．现有甲、乙两种客车，它们的载客量和租金如表所示：
（1）参加此次研学活动的师生人数是多少？原计划租用多少辆45座客车？
（2）若该校计划租用甲、乙两种客车，共12辆，且每人都有座位，则有哪几种租车方案？请你帮助计算本次研学应该怎样租车才最合算，最少租金是多少？
24．（12分）（2024•南关区一模）如图，在中，，是的角平分线，点是的中点．过点作，作射线交于点，连结．
（1）求证：四边形是矩形．
（2）若，，直接写出矩形的面积．
25．（12分）（2024•唐山一模）如图，在平面直角坐标系中，线段的两个端点坐标分别为，，点是的中点，点与点关于轴对称，直线的关系式为．
（1）若直线经过点，求直线的关系式；
（2）在（1）的条件下，若将直线向左平移个单位长度，且平移后的直线经过点，求的值；
（3）直线经过点，且与线段有交点（包含，点），请直接写出的取值范围．
参考答案
一、选择题（共10小题，满分30分，每小题3分）
1．【答案】
【解答】解：的倒数是5．
故选：．
2．【答案】
【解答】解：．
故选：．
3．【答案】
【解答】解：连接，
是正三角形，
，
，
，
，
，
故选：．
4．【答案】
【解答】解：，
选项不符合题意；
，
选项不符合题意；
，
选项符合题意；
，
选项不符合题意；
故选：．
5．【答案】
【解答】解：从上面看，是一个矩形，矩形的左侧有一条纵向的实线，右侧有一条纵向的虚线．
故选：．
6．【答案】
【解答】解：取的中点，则，连接，
，
，
又，
，
，
点在以为直径的圆上运动，
当点，点，点三点共线时，有最小值，
，，
，
的最小值为，
故选：．
7．【答案】
【解答】解：由作图可知，，为的平分线，
．
，
，
，．
，，
，
，
，
，
，
，
故选项正确，不符合题意；
，
，
，
，
，
，
，
故选项正确，不符合题意，选项正确，不符合题意；
，，
，
故选项不正确，符合题意．
故选：．
8．【答案】
【解答】解：设，
图象过，
，
，
蓄电池的电压是，
、错误，不符合题意；
当时，（A），
错误，不符合题意；
当时，，
由图象知：当时，，
正确，符合题意；
故选：．
9．【答案】
【解答】解：由题意，对称轴是直线，，
当时，随的增大而增大．
，抛物线过点，
当时，故①正确．
，
抛物线开口向下．
又点，，均在该二次函数图象上，且点到对称轴的距离最大，点到对称轴的距离最小，
，②错误．
方程的两实数根为，，
抛物线与直线的交点的横坐标为，．
由抛物线对称性可得抛物线与轴另一交点坐标为，
抛物线与轴交点坐标为，，
抛物线开口向下，，
，，故③正确．
，
．
，
，
抛物线的最大值为，
若为任意实数，则，
，故④正确．
故选：．
10．【答案】
【解答】解：当时，，则，
当，，
则，
在中，，
，
，
则，
，
故选：．
二、填空题（共6小题，满分18分，每小题3分）
11．【答案】．
【解答】解：由题意得：且，
解得：，
故答案为：．
12．【答案】．
【解答】解：反比例函数的图象在每一象限内，的值随值的增大而减小，
，
解得．
故答案为：．
13．【答案】．
【解答】解：原式
，
故答案为：．
14．【答案】①②③．
【解答】解：根据折线统计图，可知
①2030年间接经济产出比直接经济产出多（万亿元），故①正确；
②2020年到2030年，直接经济产出和间接经济产出都是逐年增长，故②正确；
③2030年直接经济产出约为2020年直接经济产出6.4万亿元万亿元倍，故③正确；
④2022年到2023年间接经济产出的增长率：，2023年到2024年间接经济产出的增长率，故④推断不合理．
故答案为：①②③．
15．【答案】．
【解答】解：如图，
连接、，交于点，
点是弧中点，，
，且，
，
，
，
，
故圆心到弦的距离为．
故答案为：．
16．【答案】10．
【解答】解：是的中位线，，
，，
，
，即，
解得：，
，
故答案为：10．
三、解答题（共9小题，满分72分）
17．
【解答】解：方程分解因式得：，
可得或，
解得：，．
18．【答案】证明见解析部分．
【解答】证明：，
，，
，
，
在和中，
，
，
．
19．【答案】（1）；（2）18．
【解答】解：（1）
；
（2），是方程的两个根，
，
．
20．【答案】（1）详见解答；
（2）980人．
【解答】解：（1）的频数为，补全频数分布直方图如下：
（2）（人，
答：估计劳动素养为优良的人数为980人．
21．【答案】．
【解答】（1）证明：如图，连结，
，
，，
，
，
，
是的半径，且，
直线是的切线．
（2）解：如图，是的直径，且于点，
，
，，
，
，
，
．
22．【答案】（1）该品牌电动车电池的电压为；
（2）电阻值的范围是．
【解答】解：（1）由电流（单位：与电阻（单位：是反比例函数关系，设，
把代入得：，
解得，
该品牌电动车电池的电压为；
（2）由（1）知，
当时，，
当时，，
电阻值的范围是．
23．【答案】（1）参加此次研学活动的师生人数是600人，原计划租用13辆甲型客车；
（2）共有九种方案，分别为当甲型客车0辆，则乙型客车12辆，当甲型客车1辆，则乙型客车11辆，当甲型客车2辆，则乙型客车10辆，当甲型客车3辆，则乙型客车9辆，当甲型客车4辆，则乙型客车8辆，当甲型客车5辆，则乙型客车7辆，当甲型客车6辆，则乙型客车6辆，当甲型客车7辆，则乙型客车5辆，当甲型客车8辆，则乙型客车4辆，租金的最小值为3200元．
【解答】解：（1）设参加此次研学活动的师生人数是人，原计划租用辆甲型客车．
根据题意，得，
解：，
答：参加此次研学活动的师生人数是600人，原计划租用13辆甲型客车；
（2）设甲型客车辆，则乙型客车辆，
由题意可得：，
，
为非负整数，
，1，2，3，4，5，6，7，8，
即共有九种方案，
当甲型客车0辆，则乙型客车12辆，
当甲型客车1辆，则乙型客车11辆，
当甲型客车2辆，则乙型客车10辆，
当甲型客车3辆，则乙型客车9辆，
当甲型客车4辆，则乙型客车8辆，
当甲型客车5辆，则乙型客车7辆，
当甲型客车6辆，则乙型客车6辆，
当甲型客车7辆，则乙型客车5辆，
当甲型客车8辆，则乙型客车4辆，
租金，
当时，租金的最小值为3200元，
答：共有九种方案，分别为当甲型客车0辆，则乙型客车12辆，当甲型客车1辆，则乙型客车11辆，当甲型客车2辆，则乙型客车10辆，当甲型客车3辆，则乙型客车9辆，当甲型客车4辆，则乙型客车8辆，当甲型客车5辆，则乙型客车7辆，当甲型客车6辆，则乙型客车6辆，当甲型客车7辆，则乙型客车5辆，当甲型客车8辆，则乙型客车4辆，租金的最小值为3200元．
24．【答案】（1）证明见解析；
（2）60．
【解答】（1）证明：，
，
点是的中点，
，
在和中，
，
，
，
，
四边形是平行四边形，
，是的角平分线，
，
，
平行四边形是矩形；
（2）解：，是的角平分线，
，，
，
，
．
25．【答案】（1）；
（2）；
（3）是．
【解答】解：（1）点与点关于轴对称，，
，
直线的解析式为，且经过点，
，解得，
直线解析式为；
（2）由（1）知直线的解析式为，
，，
线段的中点为，
设平移后的直线的解析式为，
将代入得，
解得；
（3）直线经过点，且与线段有交点（包含，点），
当直线与线段交于点时，
，解得，
直线；
当直线与线段交于点时，
，解得，
直线；
的取值范围是．

菁优网APP 菁优网公众号 菁优网小程序甲型客车
乙型客车
载客量（人辆）
45
60
租金（元辆）
250
300