

山东省青岛市即墨区2023-2024学年八年级下学期期中数学试题
展开
这是一份山东省青岛市即墨区2023-2024学年八年级下学期期中数学试题,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
友情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
本试题共24道题.第1—10题为选择题,共30分;第11—16题为填空题,共18分;第17—24题为解答题,共72分.要求所有题目均在答题卡上作答,在本卷上作答无效.
第Ⅰ卷(共30分)
一、选择题(本题满分30分,共有10道小题,每小题3分)
下列每小题都给出标号为A、B、C、D的四个结论,其中只有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.
1.下列生活垃圾分类标志中,既是轴对称图形又是中心对称图形的是( )
A.B.C.D.
2.下列等式从左到右的变形,属于因式分解的是( )
A.B.
C.D.
3.若,则下列式子错误的是( )
A.B.C.D.
4.已知点在第二象限,则m的取值范围在数轴上表示正确的是( )
A.B.C.D.
5.用反证法证明命题“在直角三角形中,至少有一个锐角不大于”时,首先应假设这个直角三角形中( )
A.两个锐角都大于B.两个锐角都小于
C.两个锐角都不大于D.两个锐角都等于
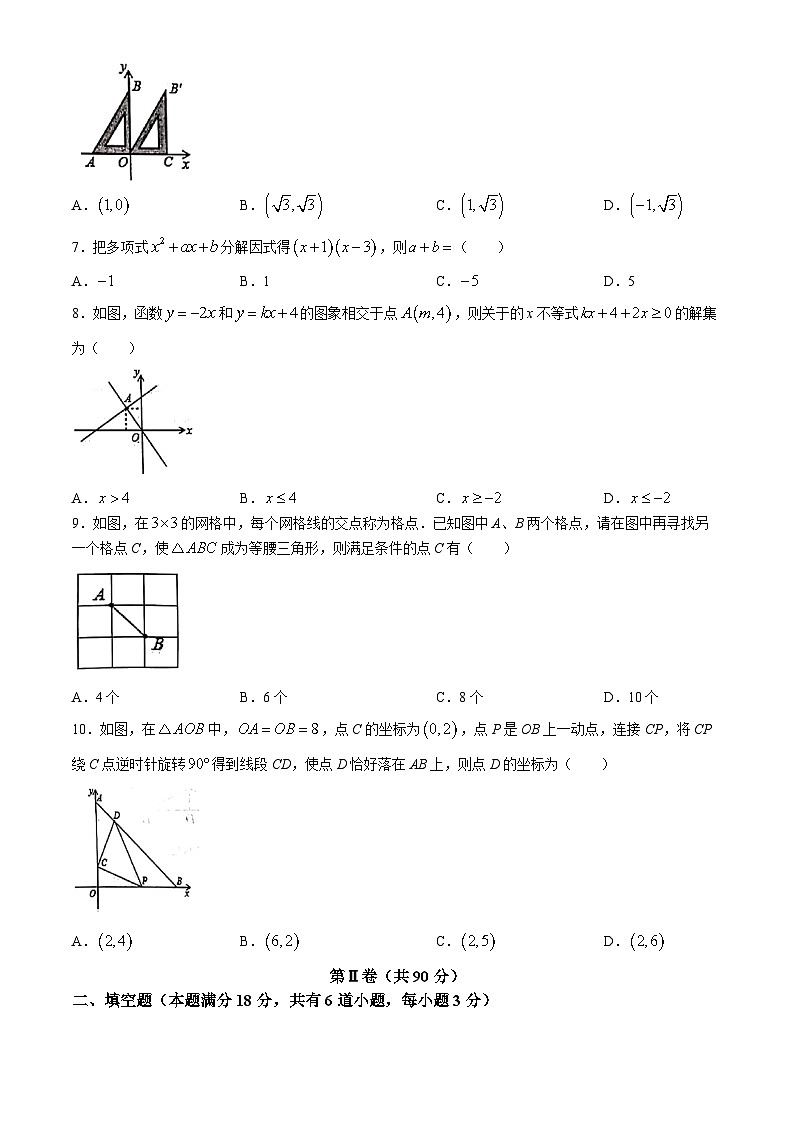
6.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为,.现将该三角板向右平移使点A与点O重合,得到,则点B的对应点的坐标是( )
A.B.C.D.
7.把多项式分解因式得,则( )
A.B.1C.D.5
8.如图,函数和的图象相交于点,则关于的x不等式的解集为( )
A.B.C.D.
9.如图,在的网格中,每个网格线的交点称为格点.已知图中A、B两个格点,请在图中再寻找另一个格点C,使成为等腰三角形,则满足条件的点C有( )
A.4个B.6个C.8个D.10个
10.如图,在中,,点C的坐标为,点P是OB上一动点,连接CP,将CP绕C点逆时针旋转得到线段CD,使点D恰好落在AB上,则点D的坐标为( )
A.B.C.D.
第Ⅱ卷(共90分)
二、填空题(本题满分18分,共有6道小题,每小题3分)
11.若等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边长为______.
12.不等式组的解集是,那么a的取值范围是______.
13.将点向下平移1个单位,向左平移3个单位得到点Q,点Q恰好落在y轴上,则点Q的坐标是______.
14.如图,在中,边AB的垂直平分线分别交AB、AC于点D,E,若,的周长为38,则的周长为______.
15.如图,四边形ABCD中,,连接AC,将绕点B逆时针旋转,点C的对应点与点D重合得到,若,,则AC的长度为______.
16.如图,已知等腰,,,于点D,点P是BA延长线上一点,点O是线段AD上一点,,下面结论:①;②;③;④.其中正确的有______个.
三、解答题(本题满分72分)
17.(本题满分4分)如图所示,已知线段a,b,求作等腰三角形,使腰长为b,底上的高为a(,尺规作图,不写作法,保留作图痕迹).
18.(本题满分16分,每题4分)
分解因式:(1)(2)
解不等式(组):(3)(4)解不等式组:,并写出其整数解.
19.(本小题6分)如图,在平面直角坐标系中,已知的三个顶点坐标分别是,,.
(1)将向左平移5个单位得到,则的坐标为(______,______);
(2)将绕点O顺时针旋转后得到,画出,并写出的坐标为(______,______);
(3)若点P为y轴上一动点,求的最小值.
20.(本题满分8分)如图,“五一”期间,小明一家乘坐高铁前往青岛旅游,计划第二天租用新源汽车去中山公园看樱花.
根据以上信息,解答下列问题:
(1)设租车时间为x小时,租用甲公司的车所需费用为y元,租用乙公司的车所需费用为元,分别求出片,关于x的函数表达式;
(2)当租车时间为多少小时,两种方案所需费用相同;
(3)根据(2)的计算结果,结合图象,请你帮助小明选择怎样的出游方案更合理.
21.(本题满分8分)如图,AD平分,,,垂足分别为点E,F,.
(1)求证:;
(2)如果,,求证:.
22.(本题满分10分)阅读下列材料:
材料1
将一个形如的二次三项式因式分解时,如果能满足且,则可以把因式分解成,
(1);(2),
材料2
因式分解:.
解:将“”看成一个整体,令,则原式,
再将“A”还原,得:原式.
上述解题用到“整体思想”,整体思想是数学解题中常见的一种思想方法,请你解答下列问题:
(1)根据材料1,把分解因式.
(2)结合材料1和材料2,完成下面小题:
①分解因式:;②分解因式:.
23.(本题满分10分)利群商场准备购进甲、乙两种服装出售,甲种服装每件售价130元,乙种服装每件售价100元.每件甲种服装的进价比乙种服装的进价贵20元,购进3件甲种服装的费用和购进4件乙种服装的费用相等,现计划购进两种服装共100件,其中甲种服装不少于65件.
(1)甲、乙两种服装每件的进价分别是多少元?
(2)若购进这100件服装的费用不得超过7500元.
①求甲种服装最多购进多少件;
②利群商场对甲种服装每件降价元,乙种服装价格不变,如果这100件服装都可售完,那么如何进货才能获得最大利润?
24.(本题满分10分)如图,中,,,,若动点P从点C开始,按的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发1秒后,求的周长;
(2)当t为几秒时,AP平分;
(3)问t为何值时,为等腰三角形?
2023—2024学年度第二学期期中学业水平诊断性测试
八年级数学试题答案
一、选择题(共30分,每题3分)
二、填空题(共18分,每题3分)
三、解答题(本大题满分72分,共有9道大题)
17.(本题共16分,每题4分)
结论:即为所求
18.(本题满分16分)
解:(1)原式;
(2)原式
;
(3)解:去分母,得:,
去括号,得:,
移项,得:,
合并同类项,得:,
系数化为1,得:;
(4)解:解不等式①,得:,
解不等式②,得:,
则不等式组的解集为.
∴x的整数解是0、1、2
19.(本题满分6分)
(1)
(2)画出;如图,
(3)
20.(本题满分8分)
解:(1)设方案一的收费(元)与租车时间x(小时)之间的函数关系式是,
∵点,在此函数图象上,
∴,解得,
即方案一的收费 (元)与租车时间x(小时)之间的函数关系式是
;
设方案二的收费(元)与租车时间x(小时)之间的函数关系式是,
∵点在此函数图象上,
∴,得,
即方案二的收费(元)与租车时间x(小时)之间的函数关系式是;
(2)令,
解得,
答:当x为时两种方案收费相等;
(3)由(2)中的结果和图象可得,
当时,选择方案二更合算;
当时,两种方案一样;
当时,选择方案一更合算.
21.(本题满分8分)
证明:(1):AD平分,,,
∴,;
在和中,
,
∴,
∴;
(2)∵AD平分,,
∴,,
∵,
∴,,
∴,
∴,
在中,,
∴,
∴,
∵AD平分,,,
∴,
∴.
22.(本题满分10分)
解:(1);
(2)①令,
则原式,
所以;
②令,
则原式
,
所以原式
.
23.(本题满分10分)
解:(1)设乙种服装的进价为x元,则甲种服装的进价为元,根据题意,得
解得
∴.
答:甲种服装的进价为80元,乙种服装的进价为60元.
(2)①设计划购买m件甲种服装,则购买件乙种服装.根据题意得
解得,
答:甲种服装最多购进75件
②设总利润为W元,则
(1)当时,随m的增大而增大,故当时,W有最大值,故购进甲种服装75件,乙种服装25件才能获得最大利润;
(2)当时,所有进货方案获利相同;
(3)当时,,W随m的增大而减小,故当时,W有最大值,故购进甲种服装65件,乙种服装35件.
24.(本题满分10分)
解:(1)已知..,由勾股定理得:,
动点P从点C开始,按的路径运动,且速度为每秒1cm,出发2秒后,则,那么,
∵,∴由勾股定理得,
∴的周长为;
(2)如图所示,过点P作于点D,
∵,∴,
∵AP平分,∴,
在与中
∴,
∴,,
设,则,
在中,,
即:,解得:,
∴,∴;
(3)①若在P边AC上时,,
此时用的时间为3s,为等腰三角形;
若P边AB上时,有两种情况:
②若使,此时,用的时间为6s,
故时,为等腰三角形;
③若时,则,
∴P点在BC的垂直平分线上,且是的中位线,
∴,此时:.
④若,作于点D,此时D为BP中点
根据面积法求得的高CD为2.4cm,在中,,
所以,
所以P运动的路程为,
则用的时间为5.4s,为等腰三角形;
综上:或6s或6.5s或5.4s时,为等腰三角形.
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
B
D
A
C
C
C
C
D
题号
11
12
13
14
15
16
答案
3cm
28
①②③④
相关试卷
这是一份山东省青岛市即墨区2023-2024学年八年级上学期期末数学试题,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份山东省青岛市即墨区2023-2024学年九年级上学期期中数学试题,共35页。试卷主要包含了选择题,填空题,作图题,解答题等内容,欢迎下载使用。
这是一份山东省青岛市即墨区2023-2024学年九年级上学期期中数学试题,共28页。试卷主要包含了选择题,填空题,作图题,解答题等内容,欢迎下载使用。









