河南省南阳市新野县2023-2024学年八年级下学期期中数学试题

这是一份河南省南阳市新野县2023-2024学年八年级下学期期中数学试题，共9页。试卷主要包含了四象限内D．若，则，解答题等内容，欢迎下载使用。

一、选择题（每小题3分，共30分）．下列各小题均有四个答案，其中只有一个是正确的．
1．若使某个分式无意义，则这个分式可以是
A．B．C．D．
2．小时候我们用肥皂水吹泡泡，泡沫的厚度约为0.000527毫米，将数据0.000527用科学记数法表示为
A．B．C．D．
3．下列各式从左到右的变形一定正确的是
A．B．C．D．
4．已知，，则
A．B．C．D．
5．如图，点A是反比例函数图象上任意一点，轴于B，点C是x轴上的动点，则的面积为
A．3B．6C．8D．不能确定
6．点M在一次函数的图象上，则点M不可能在
A．第一象限B．第二象限C．第三象限D．第四象限
7．已知反比例函数，下列结论不正确的是
A．图象必经过点B．y随x的增大而增大
C．图象在第二、四象限内D．若，则
8．若点，，都在反比例函数的图象上，则，，的大小关系是
A．B．C．D．
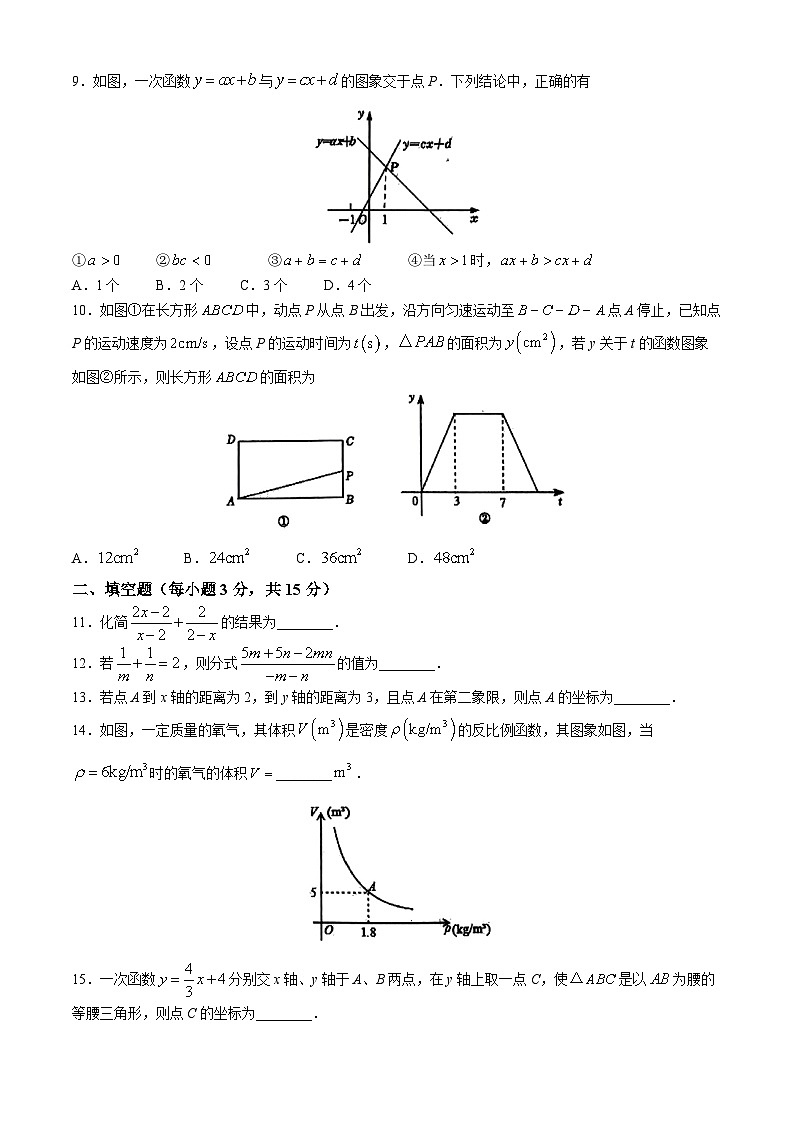
9．如图，一次函数与的图象交于点P．下列结论中，正确的有
①②③④当时，
A．1个B．2个C．3个D．4个
10．如图①在长方形中，动点P从点B出发，沿方向匀速运动至点A停止，已知点P的运动速度为，设点P的运动时间为，的面积为，若y关于t的函数图象如图②所示，则长方形的面积为
A．B．C．D．
二、填空题（每小题3分，共15分）
11．化简的结果为________．
12．若，则分式的值为________．
13．若点A到x轴的距离为2，到y轴的距离为3，且点A在第二象限，则点A的坐标为________．
14．如图，一定质量的氧气，其体积是密度的反比例函数，其图象如图，当时的氧气的体积________．
15．一次函数分别交x轴、y轴于A、B两点，在y轴上取一点C，使是以为腰的等腰三角形，则点C的坐标为________．
三、解答题（共8小题）
16．（8分）（1）（4分）．
（2）（4分）
17．（8分）老师在黑板上写了一个代数式的正确计算结果，随后用“黑板擦”遮住原代数式的一部分，如图：（．
（1）求被“黑板擦”遮住部分的代数式，并将其化简；
（2）原代数式的值能等于吗？请说明理由．
18．（9分）已知一次函数．
（1）在如图所示的平面直角坐标系中，画出函数的图象；
（2）图象与x轴的交点为A，则A点的坐标为________，与y轴交点为B，则B的坐标为________；
（3）在（2）的条件下，求出的面积；
（4）利用图象直接写出：当时，x的取值范围．
19．（9分）在学校开展的“劳动创造美好生活”主题活动中，八（2）班负责校园某绿化角的设计、种植与养护，同学们计划购买绿萝和吊兰两种绿植，已知吊兰的单价比绿萝的单价多5元，且用200元购买绿萝的盆数与用300元购买吊兰的盆数相同．
（1）求购买绿萝和吊兰的单价各是多少元？
（2）若购买绿萝的数量是吊兰数量的两倍，且资金不超过500元，则购买吊兰的数量最多是多少盆？
20．（9分）某地区一家供电公司为了居民能节约用电，采用分段计费的方法来计算电费．月用电量x（度）与相应电费y（元）之间的函数图象如图所示．
（1）月用电量为60度时，应交电费多少元？
（2）当时，求y与x之间的函数关系式；
（3）月用电量为150度时，应交电费多少元？
21．（10分）如图，一次函数的图象与反比例函数的图象交于，两点，与x轴相交于点C．
（1）求反比例函数的表达式；
（2）观察图象，直接写出不等式的解集；
（3）若为x轴上的一动点，连接，当的面积为3时，求点P的坐标．
22．（10分）近年来，市民交通安全意识逐步增强，头盔需求量增大．某商店欲购进甲、乙两种头盔共40只，已知甲种头盔单价是65元，乙种头盔单价是54元。购买时正好赶上厂家进行促销活动，促销方式如下：甲种头盔按单价的八折出售，乙种头盔每只降价6元出售．如果此次购买甲种头盔的数量不低于乙种头盔数量的一半，那么应购买多少只甲种头盔，使此次购买头盔的总费用最小？最小费用是多少元？
23．（12分）如图，在平面直角坐标系中，一次函数的图象（是常数且）分别与x轴和y轴交于点B和点A，一次函数的图象（是常数且）分别与x轴和y轴交于点E和点C，直线与交于点．
（1）求和的值；
（2）不等式的解集为________；方程组的解为________；
（3）若点P是直线上一点，且，求点P的坐标．
新野县2024年春期期中考试质量评估八年级数学参考答案
一、选择题（每题3分，共30分）
1、B2、C3、D4、A5、A6、B7、B8、C9、A10、D
二、填空题（每题3分，共15分）
11．212．13．14．1.515．，（各一分）
三、解答题．
16．（8分）（1）（4分）解：
（2）（4分）原式
17．（8分）解：（1）由题意得：
（2）不能，
假设能，则，
，
，
，
当时，分式，除数为零无意义，则原代数式的值不能等于．
18．（9分）解：（1）当时，当时，，
则图象如图所示
（2），，
（3）
，
（4）．
19．（9分）解：（1）设购买绿萝的单价为x元，则购买吊兰的单价为元，
由题意得：，
解得：，
经检验，是原分式方程的解，且符合题意，
则，
答：购买绿萝的单价为10元，购买吊兰的单价为15元；
（2）设购买吊兰的数量为a盆，则购买绿萝的数量为盆，
由题意得：，
解得：，
为正整数，
的最大值为14，
答：购买吊兰的数量最多是14盆．
20．（9分）解：（1）当时，设，
将代入可得：，
解得：，
当时，，
当时，，
答：月用电量为60度时，应交电费36元；
（2）当时，设，将，代入可得：
解得：，
答：当时，y与x之间的函数关系式为；
（3）当时，，
答：月用电量为150度时，应交电费130元．
21．（10分）解：（1）函数的图象经过，
，
解得：，
，
，
反比例函数表达式为：；
（2）由图可得：或；
（3）如图：
在中，当时，得，
解得：，
，
，
，
，，
，
解得：或8，
点P的坐标为或．
（备注：求出一个点P的坐标给2分）
22．（10分）解：设再次购进甲种头盔m只，总费用为w元，
根据题意，得，
解得，
，
，
随着m增大而增大，
当时，w取得最小值，
即购买14只甲种头盔时，总费用最小，最小费用为（元），
答：购买14只甲种头盔时，总费用最小，最小费用为1976元．
23．（12分）解：（1）将点分别代入一次函数和一次函数的表达式中，
得：，
解得：；
（2）
（3）由（1）可知直线的表达式为，直线的表达式为，
当时，，
解得，
，
，
当时，，
解得，
，
，
，
设点P的坐标为，
，
解得：或，
当时，；当时，，
点P的坐标为或．
（备注：求出一个点P的坐标给2分）