2023年贵州省遵义市第十一中学中考数学模拟预测题（原卷版+解析版）

这是一份2023年贵州省遵义市第十一中学中考数学模拟预测题（原卷版+解析版），文件包含2023年贵州省遵义市第十一中学中考数学模拟预测题原卷版docx、2023年贵州省遵义市第十一中学中考数学模拟预测题解析版docx等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。

一、选择题（本大题共12小题，共36.0分．在每小题列出的选项中，选出符合题目的一项）
1. 下列各数中，为无理数的是（ ）
A. B. C. 0D.
【答案】A
【解析】
【分析】根据无理数的定义逐项判断即可．
【详解】A、是无理数，符合题意；
B、小数点后的是无限循环的，则是有理数，不符题意；
C、0是整数，属于有理数，不符题意；
D、是有理数，不符题意,
故选：A．
【点睛】本题考查了无理数的定义，熟记定义是解题关键．
2. 某几何体如图所示，它的俯视图是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】根据从上面看得到的图形是俯视图，即可得答案．
【详解】解：从上面看，是两个圆形，大圆内部有个小圆．
故选：D．
【点睛】本题考查了简单组合体的三视图，解题的关键是掌握从上面看得到的图形是俯视图．
3. 袁隆平院士被誉为“杂交水稻之父”，经过他带领的团队多年艰苦努力，目前我国杂交水稻种植面积达2.4亿亩，每年增产的粮食可以养活80000000人．将80000000这个数用科学记数法可表示为，则的值是（ ）
A. 6B. 7C. 8D. 9
【答案】B
【解析】
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
【详解】解：∵80000000＝8×107，
∴n＝7，
故选：B．
【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
4. 若关于的一元二次方程 的一个根是2，则的值为（ ）
A. 2B. 3C. 4D. 5
【答案】D
【解析】
【分析】根据韦达定理，可知另一个根为，再根据韦达定理可知的值为根之和，即可求得
【详解】的一个根为2，设另一根为
，解得
又
故选D
【点睛】本题考查了一元二次方程根与系数的关系即韦达定理，熟悉韦达定理是解题的关键．
5. 今年是三年禁毒“大扫除”攻坚克难之年．为了让学生认识毒品的危害，某校举办了禁毒知识比赛，小红所在班级学生的平均成绩是80分，小星所在班级学生的平均成绩是85分，在不知道小红和小星成绩的情况下，下列说法比较合理的是（ ）
A. 小红的分数比小星的分数低B. 小红的分数比小星的分数高
C. 小红的分数与小星的分数相同D. 小红的分数可能比小星的分数高
【答案】D
【解析】
【分析】根据平均数的意义，逐一判断选项，即可．
【详解】解：∵平均数不能代表每组数据中的具体哪个数，
∴小红的分数和小星的分数并不能确定哪个分数高或低，
∴小红的分数可能比小星的分数高，
故选D．
【点睛】本题主要考查平均数的意义，掌握” 平均数不能代表每组数据中的具体哪个数，只能反映数据集中趋势“，是解题的关键．
6. 计算的结果，正确的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】化简二次根式并代入特殊角的锐角三角比，再按照正确的运算顺序进行计算即可．
【详解】解：
＝
＝
＝．
故选：B
【点睛】此题考查了二次根式的运算、特殊角的锐角三角比等知识，熟练掌握运算法则是解题的关键．
7. 如图，拦水坝的横断面为梯形，其中，，，斜坡长，则斜坡的长为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题解直角三角形的应用，正确作出辅助线，构造出直角三角形是解决问题的关键．过作于，过作于，则，在中，根据锐角三角函数求出，在中，根据角的直角三角形的性质求出．
【详解】解：过作于，过作于，
，
，
，
在中，
，
在中，
，
，
，
故选：B．
8. 如图，是内一点，，，，，，，，分别是，，，的中点，则四边形的周长为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查了三角形的中位线定理，勾股定理，解题的关键是熟练掌握三角形的中位线定理．由，，，根据勾股定理可求出，根据，，，分别是，，，的中点，结合中位线定理即可求解．
【详解】解：，，，，，
，
，，，分别是，，，的中点，
，，，，
四边形的周长为：，
故选：A．
9. 如图，一件扇形艺术品完全打开后，夹角为，的长为，扇面的长为，则扇面的面积是（ ）
A. 375πcm2B. 450πcm2C. 600πcm2D. 750πcm2
【答案】C
【解析】
【分析】根据扇形的面积公式，利用减去即可得扇面的面积．
【详解】解：cm，cm
cm
=cm2．
故选：C
【点睛】本题主要考查了扇形的面积公式，熟知扇形面积公式并能够将不规则图形的面积转化为已学图形的面积是解决本题的关键．
10. 如图，正方形ABCD中，AB＝6，E为AB的中点，将△ADE沿DE翻折得到△FDE，延长EF交BC于G，FH⊥BC，垂足为H，连接BF、DG.以下结论：①BF∥ED；②△DFG≌△DCG；③△FHB∽△EAD；④tan∠GEB＝；⑤S△BFG＝2.6；其中正确的个数是( )
A. 2B. 3C. 4D. 5
【答案】C
【解析】
【分析】利用正方形性质和折叠的性质可得∠AED＝∠FED，AD＝FD，AE＝EF，∠A＝∠DFE，即可判定①；证明Rt△DFG≌Rt△DCG，即可判定②；证明△FHB∽△EAD，即可判定③；设FG＝CG＝x，则BG＝6﹣x，EG＝3+x，再利用勾股定理即可判定④；设FH＝a，则HG＝4﹣2a，再利用勾股定理即可判定⑤
【详解】∵正方形ABCD中，AB＝6，E为AB的中点
∴AD＝DC＝BC＝AB＝6，AE＝BE＝3，∠A＝∠C＝∠ABC＝90°
∵△ADE沿DE翻折得到△FDE
∴∠AED＝∠FED，AD＝FD＝6，AE＝EF＝3，∠A＝∠DFE＝90°
∴BE＝EF＝3，∠DFG＝∠C＝90°
∴∠EBF＝∠EFB
∵∠AED+∠FED＝∠EBF+∠EFB
∴∠DEF＝∠EFB
∴BF∥ED
故结论①正确；
∵AD＝DF＝DC＝6，∠DFG＝∠C＝90°，DG＝DG
∴Rt△DFG≌Rt△DCG
∴结论②正确；
∵FH⊥BC，∠ABC＝90°
∴AB∥FH，∠FHB＝∠A＝90°
∵∠EBF＝∠BFH＝∠AED
∴△FHB∽△EAD
∴结论③正确；
∵Rt△DFG≌Rt△DCG
∴FG＝CG
设FG＝CG＝x，则BG＝6﹣x，EG＝3+x
在Rt△BEG中，由勾股定理得：32+(6﹣x)2＝(3+x)2
解得：x＝2
∴BG＝4
∴tan∠GEB＝
故结论④正确；
∵△FHB∽△EAD，且
∴BH＝2FH
设FH＝a，则HG＝4﹣2a
在Rt△FHG中，由勾股定理得：a2+(4﹣2a)2＝22
解得：a＝2(舍去)或a＝
∴S△BFG＝×4×＝2.4
故结论⑤错误；
故选C.
【点睛】此题考查正方形的性质，折叠的性质，三角形全等的判定与性质，勾股定理，解题关键真题掌握各性质
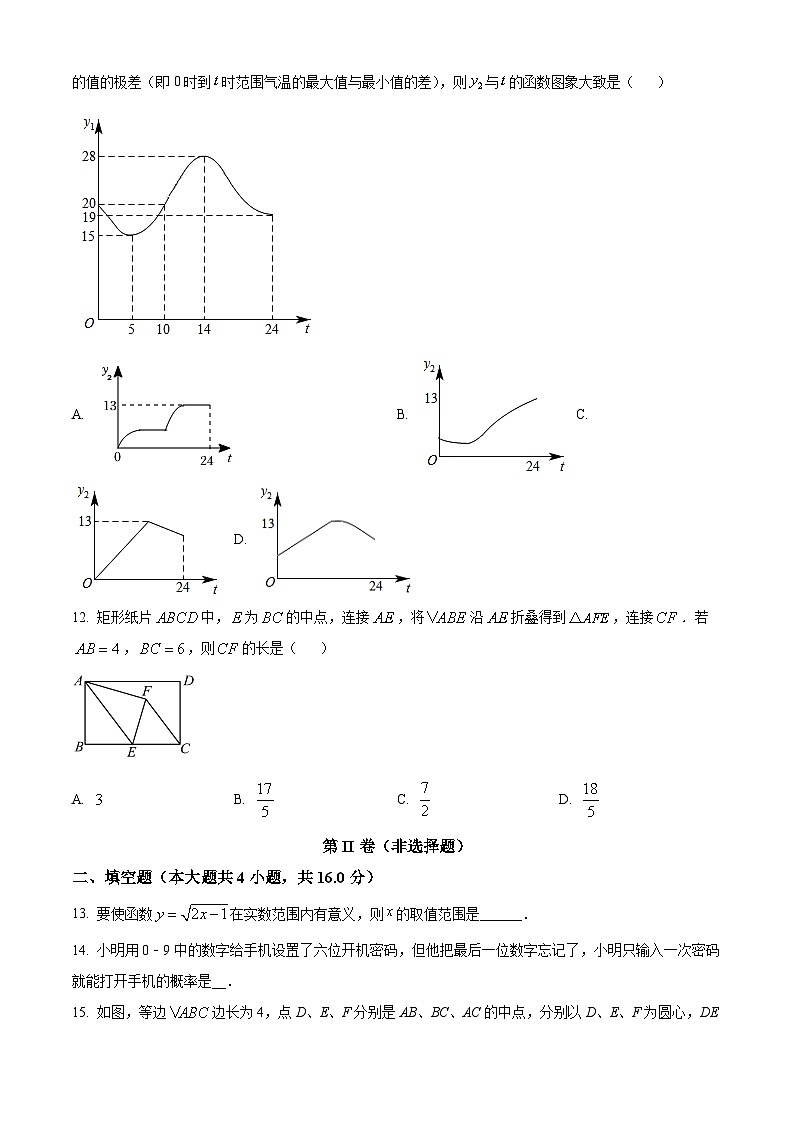
11. 遵义市某天的气温（单位：℃）随时间（单位：）的变化如图所示，设表示0时到时气温的值的极差（即0时到时范围气温的最大值与最小值的差），则与的函数图象大致是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】根据函数图象逐段分析，进而即可求解．
【详解】解：∵根据函数图象可知，从0时至5时，先变大，从5到10时，的值不发生变化
大概12时后变大，从14到24时，不变，
∴的变化规律是，先变大，然后一段时间不变又变大，最后不发生变化，
反映到函数图象上是先升，然后一段平行于的线段，再升，最后不变
故选A
【点睛】本题考查了函数图象，极差，理解题意是解题的关键．
12. 矩形纸片中，为的中点，连接，将沿折叠得到，连接．若，，则的长是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】连接，交于点，根据翻折的性质知，，，垂直平分，说明，利用等积法求出的长，再利用勾股定理可得答案．
【详解】解：连接，交于点，
在矩形中，，，
∴，
∵将沿折叠得到，
∴，，，
∴垂直平分，
∴，，
∵点为的中点，，，
∴，
∴，
∵，
∴，
∴，
∴，
在中，，
∵，
∴，
∴，
在中，，
故选：D．
【点睛】本题考查翻折变换，矩形的性质，垂直平分线的判定和性质，平行线的判定和性质，勾股定理等知识，利用等积法求出的长是解题的关键．
第II卷（非选择题）
二、填空题（本大题共4小题，共16.0分）
13. 要使函数在实数范围内有意义，则的取值范围是______．
【答案】
【解析】
【分析】本题考查的是函数自变量的取值范围的确定，熟记二次根式的被开方数是非负数是解题的关键．
根据二次根式的被开方数是非负数列出不等式，解不等式得到答案．
【详解】解：由题意得：，
解得：，
故答案为：．
14. 小明用0﹣9中的数字给手机设置了六位开机密码，但他把最后一位数字忘记了，小明只输入一次密码就能打开手机的概率是__．
【答案】．
【解析】
【分析】根据最后一个数字可能是0～9中任一个．总共有十种情况，其中开锁只有一种情况．利用概率公式进行计算即可．
【详解】随意拨动最后一位号码正好开锁的概率是：．故答案为．
【点睛】本题考查了概率公式．如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．
15. 如图，等边边长为4，点D、E、F分别是AB、BC、AC的中点，分别以D、E、F为圆心，DE长为半径画弧，围成一个曲边三角形，则曲边三角形的周长为______．
【答案】
【解析】
【分析】证明△DEF是等边三角形，求出圆心角的度数，利用弧长公式计算即可．
【详解】解：连接EF、DF、DE，
∵等边边长为4，点D、E、F分别是AB、BC、AC的中点，
∴是等边三角形，边长为2，
∴∠EDF=60°，
弧EF的长度为，同理可求弧DF、DE的长度为，
则曲边三角形的周长为；
故答案：．
【点睛】本题考查了等边三角形的性质与判定和弧长计算，中位线的性质，解题关键是熟记弧长公式，正确求出圆心角和半径．
16. 如图，在正方形中，，P为对角线上一动点，F为射线上一点，若，则的面积的最大值为________．
【答案】16
【解析】
【分析】本题考查了正方形的性质，等腰三角形的性质，二次函数的最值等知识点，作于M，根据正方形的性质易得，设，则，根据等腰三角形的性质即可得出，由三角形面积公式得出，根据二次函数的性质即可求得结果，熟练掌握二次函数的性质是解题的关键．
【详解】如图，过点P作于M，
∵是正方形的对角线，
∴，
∴是等腰直角三角形，
∴，
设，则，
∵，
∴，
∴，
∵，
∴，
∴当时，有最大值，且最大值为16．
故答案为：16．
三、计算题（本大题共2小题，共10.0分）
17. 计算：2sin60°+|2|+（﹣1）﹣1
【答案】3.
【解析】
【分析】首先计算乘方，然后计算乘法，最后从左向右依次计算，求出算式的值是多少即可．
【详解】2sin60°+|2|+（﹣1）﹣1
＝221﹣（﹣2）
21
＝3.
【点睛】本题考查了实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．
18. 化简式子（1），并在﹣2，﹣1，0，1，2中选取一个合适的数作为a的值代入求值．
【答案】，1.
【解析】
【分析】根据分式的加法和除法可以化简题目中的式子，然后从-2，-1，0，1，2中选取一个使得原分式有意义的值代入化简后的式子即可解答即可．
【详解】（1）
＝[]
＝（）


，
当a＝﹣2时，原式1．
【点睛】本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．
四、解答题（本大题共8小题，共88.0分．解答应写出文字说明，证明过程或演算步骤）
19. 电子政务、数字经济、智慧社会一场数字革命正在神州大地激荡．在第二届数字中国建设峰会召开之际，某校举行了第二届“掌握新技术，走进数时代”信息技术应用大赛，将该校八年级参加竞赛的学生成绩统计后，绘制成如下统计图表（不完整）：
“掌握新技术，走进数时代”信息技术应用大赛成绩频数分布统计表
请观察上面图表，解答下列问题：
（1）统计表中m＝ ；统计图中n＝ ，D组的圆心角是 度．
（2）D组的4名学生中，有2名男生和2名女生．从D组随机抽取2名学生参加5G体验活动，请你画出树状图或用列表法求：
①恰好1名男生和1名女生被抽取参加5G体验活动的概率；
②至少1名女生被抽取参加5G体验活动的概率．
【答案】（1）20、32、28.8；（2）①恰好1名男生和1名女生被抽取参加5G体验活动的概率为；②至少1名女生被抽取参加5G体验活动的概率为．
【解析】
【分析】（1）先根据A组人数及其所占百分比求出总人数，由各组人数之和等于总人数求出B组人数m的值，用360°乘以D组人数所占比例可得；
（2）列表得出所有等可能结果，从中找到符合条件的结果数，再根据概率公式计算可得．
【详解】（1）被调查的总人数为10÷20%＝50，
则m＝50﹣（10+16+4）＝20，
n%100%＝32%，即n＝32，
D组的圆心角是360°28.8°，
故答案为20、32、28.8；
（2）①设男同学标记为A、B；女学生标记为1、2，可能出现的所有结果列表如下：
共有 12 种可能的结果，且每种的可能性相同，其中刚好抽到一男一女的结果有8种，
∴恰好1名男生和1名女生被抽取参加5G体验活动的概率为；
②∵至少1名女生被抽取参加5G体验活动的有10种结果，
∴至少1名女生被抽取参加5G体验活动的概率为．
【点睛】本题考查了频数分布表，解题的关键是明确题意，找出所求问题需要的条件，利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题，也考查了列表法和画树状图求概率．
20. 如图，PA是以AC为直径的☉O的切线，切点为A，过点A作AB⊥OP，交☉O于点B．
（1）求证：PB是☉O的切线；
（2）若AB＝6，，求PO的长．
【答案】（1）见解析；（2）
【解析】
【分析】（1）连接OB，根据切线的性质和垂径定理得到∠POA＝∠POB，然后根据证明△PAO△PBO，然后根据全等三角形的性质即可证明；
（2）根据垂径定理得到DA＝DB＝3，然后根据余弦的定义得到PA＝5，进而应用勾股定理即可求解，然后对继续应用余弦的定义得到，即可最终求解PO的长．
【详解】（1）证明：连接OB，
∵PA是以AC为直径的☉O的切线，切点为A，
∴∠PAO＝，
∵OA＝OB，AB⊥OP，
∴∠POA＝∠POB，
又OP＝OP，
∴△PAO△PBO，
∴∠PBO＝∠PAO＝，
即OB⊥PB，
∴PB是☉O的切线；
（2）解：设OP与AB交于点D．
，
∵AB⊥OP，AB＝6，
∴DA＝DB＝3，∠PDA＝∠PDB＝，
∵，
∴PA＝5，∴PD＝，
在Rt△APD和Rt△APO中，
∵，
∴，
∴．
【点睛】本题考查了切线的判定和性质，解直角三角形，余弦的定义，关键是通过余弦的定义建立等量关系进行求解．
21. 2022北京冬奥会期间，某网店直接从工厂购进A、B两款冰墩墩钥匙扣，进货价和销售价如下表：（注：利润=销售价-进货价）
（1）网店第一次用850元购进A、B两款钥匙扣共30件，求两款钥匙扣分别购进的件数；
（2）第一次购进的冰墩墩钥匙扣售完后，该网店计划再次购进A、B两款冰墩墩钥匙扣共80件（进货价和销售价都不变），且进货总价不高于2200元．应如何设计进货方案，才能获得最大销售利润，最大销售利润是多少？
（3）冬奥会临近结束时，网店打算把B款钥匙扣调价销售．如果按照原价销售，平均每天可售4件．经调查发现，每降价1元，平均每天可多售2件，将销售价定为每件多少元时，才能使B款钥匙扣平均每天销售利润为90元？
【答案】（1）A、B两款钥匙扣分别购进20件和10件
（2）购进A款冰墩墩钥匙扣40件，购进B款冰墩墩钥匙扣40件时利润最大，最大为1080元
（3）销售价定为每件30元或34元时，才能使B款钥匙扣平均每天销售利润为90元
【解析】
【分析】(1)设A、B两款钥匙扣分别购进x和y件，根据“用850元购进A、B两款钥匙扣共30件”列出二元一次方程组即可求解；
(2)设购进A款冰墩墩钥匙扣m件，则购进B款冰墩墩钥匙扣(80-m)件，根据“进货总价不高于2200元”列出不等式求出；设销售利润为元，得到，随着m的增大而增大，结合m的范围由此即可求出最大利润；
(3)设B款冰墩墩钥匙扣降价a元销售，则平均每天多销售2a件，每天能销售(4+2a)件，每件的利润为(12-a)元，由“平均每天销售利润为90元”得到(4+2a)(12-a)=90，求解即可．
【小问1详解】
解：设A、B两款钥匙扣分别购进x和y件，
由题意可知： ，
解出：，
故A、B两款钥匙扣分别购进20和10件．
【小问2详解】
解：设购进A款冰墩墩钥匙扣m件，则购进B款冰墩墩钥匙扣(80-m)件，
由题意可知：，
解出：，
设销售利润为元，则，
∴是关于m的一次函数，且3＞0，
∴随着m的增大而增大，
当时，销售利润最大，最大为元，
故购进A款冰墩墩钥匙扣40件，购进B款冰墩墩钥匙扣40件时利润最大，最大为1080元．
小问3详解】
解：设B款冰墩墩钥匙扣降价a元销售，则平均每天多销售2a件，每天能销售(4+2a)件，每件的利润为(12-a)元，
由题意可知：(4+2a)(12-a)=90，
解出：a1=3，a2=7，
故B款冰墩墩钥匙扣售价为34元或30元一件时，平均每天销售利润为90元．
【点睛】本题考查了二元一次方程组、一元一次不等式的应用、一次函数增减性求利润最大问题及一元二次方程的应用，属于综合题，读懂题意是解决本题的关键．
22. 交通安全心系千万家．高速公路管理局在某隧道内安装了测速仪，如图所示的是该段隧道的截面示意图．测速仪和测速仪到路面之间的距离，测速仪和之间的距离，一辆小汽车在水平的公路上由西向东匀速行驶，在测速仪处测得小汽车在隧道入口点的俯角为25°，在测速仪处测得小汽车在点的俯角为60°，小汽车在隧道中从点行驶到点所用的时间为38s（图中所有点都在同一平面内）．
（1）求，两点之间的距离（结果精确到1m）；
（2）若该隧道限速22m/s，判断小汽车从点行驶到点是否超速？通过计算说明理由．（参考数据：，，，，，）
【答案】（1）760米
（2）未超速，理由见解析
【解析】
【分析】（1）分别解，求得，根据即可求解；
（2）根据路程除以速度，进而比较即可求解．
【小问1详解】
四边形是平行四边形
四边形是矩形，
在中，
在中，
答：，两点之间的距离为760米；
【小问2详解】
，
小汽车从点行驶到点未超速．
【点睛】本题考查了解直角三角形的应用，掌握直角三角形中的边角关系是解题的关键．
23. 如图1，在四边形中，和相交于点O，．
（1）求证：四边形是平行四边形；
（2）如图2，E，F，G分别是的中点，连接，若，求的周长．
【答案】（1）证明过程见解析
（2）24
【解析】
【分析】(1)由得到BC//AD，再证明△AOD≌△COB得到BC=AD，由此即可证明四边形ABCD为平行四边形；
(2)由ABCD为平行四边形得到BD=2BO，结合已知条件BD=2BA得到BO=BA=CD=OD，进而得到△DOF与△BOA均为等腰三角形，结合F为OC中点得到∠DFA=90°，GF为Rt△ADF斜边上的中线求出；过B点作BH⊥AC于H，求出BH=9，再证明四边形BHGE为平行四边形得到GE=BH=9，最后将GE、GF、EF相加即可求解．
【小问1详解】
证明：∵，
∴BC∥AD，
在△AOD和△COB中：，
∴△AOD≌△COB(ASA)，
∴BC=AD，
∴四边形ABCD为平行四边形．
【小问2详解】
解：∵点E、F分别为BO和CO的中点，
∴EF是△OBC的中位线，
∴；
∵ABCD为平行四边形，
∴BD=2BO，
又已知BD=2BA，
∴BO=BA=CD=OD，
∴△DOC与△BOA均为等腰三角形，
又F为OC的中点，连接DF，
∴DF⊥OC，
∴∠AFD=90°，
又G为AD的中点，
由直角三角形斜边上中线等于斜边的一半可知：；
过B点作BH⊥AO于H，连接HG，如上图所示：
由等腰三角形的“三线合一”可知：AH=HO=AO=AC=4，
∴HC=HO+OC=4+8=12，
在Rt△BHC中，由勾股定理可知,
∵H为AO中点，G为AD中点，
∴HG为△AOD的中位线，
∴HG∥BD，即HG∥BE，
且，
∴四边形BHGE为平行四边形，
∴GE=BH=9，
∴．
【点睛】本题考查了三角形全等的判定方法、平行四边形的性质、三角形中位线定理、直角三角形斜边上的中线等于斜边的一半等，熟练掌握各图形的性质及定理是解决本题的关键．
24. 如图，正六边形ABCDEF内接于⊙O，BE是⊙O的直径，连接BF，延长BA，过F作FG⊥BA，垂足为G.
(1)求证：FG是⊙O的切线；
(2)已知FG＝2，求图中阴影部分的面积.
【答案】(1)见解析；(2) 图中阴影部分的面积为.
【解析】
【分析】（1）连接OF，AO，根据题意可得∠ABF＝∠AFB＝∠EBF＝30°，再利用OB＝OF，证明AB∥OF，即可解答
（2）先利用等弧对等角求出△AOF是等边三角形，再证明S△ABF＝S△AOF，即可解答
【详解】(1)证明：连接OF，AO，
∵AB＝AF＝EF，
∴，
∴∠ABF＝∠AFB＝∠EBF＝30°，
∵OB＝OF，
∴∠OBF＝∠BFO＝30°，
∴∠ABF＝∠OFB，
∴AB∥OF，
∵FG⊥BA，
∴OF⊥FG，
∴FG是⊙O的切线；
(2)解：∵，
∴∠AOF＝60°，
∵OA＝OF，
∴△AOF是等边三角形，
∴∠AFO＝60°，
∴∠AFG＝30°，
∵FG＝2，
∴AF＝4，
∴AO＝4，
∵AF∥BE，
∴S△ABF＝S△AOF，
∴图中阴影部分的面积＝.
【点睛】此题考查切线的判定，等边三角形的判定，扇形面积，解题关键在于利用等弧对等角
25. 如图，已知抛物线y＝ax2+bx﹣1与x轴的交点为A(﹣1，0)，B(2，0)，且与y轴交于C点.
(1)求该抛物线的表达式；
(2)点C关于x轴的对称点为C1，M是线段BC1上的一个动点(不与B、C1重合)，ME⊥x轴，MF⊥y轴，垂足分别为E、F，当点M在什么位置时，矩形MFOE的面积最大？说明理由.
(3)已知点P是直线y＝x+1上的动点，点Q为抛物线上的动点，当以C、C1、P、Q为顶点的四边形为平行四边形时，求出相应的点P和点Q的坐标.
【答案】(1) ；(2)点M为线段C1B中点时，S矩形MFOE最大，理由见解析；(3) 点P和点Q的坐标为P1(4，3)，Q1(4，5)或P2(﹣2，0)，Q2(﹣2，2)或P3(2，2)，Q3(2，0)或P4(﹣2，0)，Q4(2，0).
【解析】
【分析】（1）将A(﹣1，0)，B(2，0)分别代入解析式即可解答
（2）令x＝0，y＝﹣1，得出C的坐标，再利用对称轴的性质得出C1，将B(2，0)，C1(0，1)分别代入直线C1B解析式，得出直线C1B的解析式，设M(t，)，则 E(t，0)，F(0，)，根据矩形的面积公式即可解答
（3）根据题意可分情况讨论①当C1C为边，则C1C∥PQ，C1C＝PQ，设P(m，m+1)，Q(m，)，求出m即可解答；②C1C为对角线，∵C1C与PQ互相平分，C1C的中点为(0，0)，PQ的中点为(0，0)，设P(m，m+1)，则Q(﹣m，)，求出m即可
【详解】(1)将A(﹣1，0)，B(2，0)分别代入抛物线y＝ax2+bx﹣1中，得，解得：
∴该抛物线的表达式为：.
(2)在中，令x＝0，y＝﹣1，∴C(0，﹣1)
∵点C关于x轴的对称点为C1，
∴C1(0，1)，设直线C1B解析式为y＝kx+b，将B(2，0)，C1(0，1)分别代入得，解得，
∴直线C1B解析式为，设M(t，)，则 E(t，0)，F(0，)
∴S矩形MFOE＝OE×OF＝t()＝﹣(t﹣1)2+，
∵﹣＜0，
∴当t＝1时，S矩形MFOE最大值＝，此时，M(1，)；即点M为线段C1B中点时，S矩形MFOE最大.
(3)由题意，C(0，﹣1)，C1(0，1)，以C、C1、P、Q为顶点的四边形为平行四边形，分以下两种情况：
①C1C为边，则C1C∥PQ，C1C＝PQ，设P(m，m+1)，Q(m，)，
∴|()﹣(m+1)|＝2，解得：m1＝4，m2＝﹣2，m3＝2，m4＝0(舍)，
P1(4，3)，Q1(4，5)；P2(﹣2，0)，Q2(﹣2，2)；P3(2，2)，Q3(2，0)
②C1C为对角线，∵C1C与PQ互相平分，C1C的中点为(0，0)，
∴PQ的中点为(0，0)，设P(m，m+1)，则Q(﹣m，)
∴(m+1)+()＝0，解得：m1＝0(舍去)，m2＝﹣2，
∴P4(﹣2，0)，Q4(2，0)；
综上所述，点P和点Q的坐标为：P1(4，3)，Q1(4，5)或P2(﹣2，0)，Q2(﹣2，2)或P3(2，2)，Q3(2，0)或P4(﹣2，0)，Q4(2，0).
【点睛】此题考查二次函数综合题，解题关键在于把已知点代入解析式求值
26. 如图1，在中，，，D为内一点，将线段AD绕点A逆时针旋转90°得到AE，连接CE，BD的延长线与CE交于点F．
（1）求证：，；
（2）如图2．连接AF，DC，已知，判断AF与DC的位置关系，并说明理由．
【答案】（1）见解析；（2），理由见解析
【解析】
【分析】（1）首先根据旋转的性质，判断出∠DAE=90°，AD=AE，进而判断出∠BAD=∠CAE；然后根据全等三角形判定的方法，判断出△ABD≌△ACE，即可判断出BD=CE．再证明，即可证明；
（2）由得 ，再证明A，D，F，E在以DE为直径的圆上，即可证明，从而可证明AF//CD．
【详解】解（1）由旋转的性质，可得∠DAE=90°，AD=AE，
∵∠BAD+∠DAC=∠BAC=90°，∠CAE+∠DAC=∠DAE=90°，
∴∠BAD=∠CAE，
在△ABD和△ACE中，
，
∴△ABD≌△ACE（SAS），
∴BD=CE，
∵
∴，即
∴
∴
∴，即;
（2），理由如下：
∵
∴
由（1）知，
∴A，D，F，E在以DE为直径的圆上，如图，
∵AD=AE
∴弧AD=弧AE，
∴
∴
∴；
【点睛】此题主要考查了旋转的性质和应用，要熟练掌握，解答此题的关键是要明确：①对应点到旋转中心的距离相等．②对应点与旋转中心所连线段的夹角等于旋转角．③旋转前、后的图形全等．另外此题还考查了全等三角形的判定和性质的应用，以及四点共圆的知识，要熟练掌握．组别
成绩x（分）
人数
A
60≤x＜70
10
B
70≤x＜80
m
C
80≤x＜90
16
D
90≤x≤100
4
A
B
1
2
A
/
（B，A）
（1，A）
（2，A）
B
（A，B）
/
（1，B）
（2，B）
1
（A，1）
（B，1）
/
（2，1）
2
（A，2）
（B，2）
（1，2）
/
类别
价格
A款钥匙扣
B款钥匙扣
进货价（元/件）
30
25
销售价（元/件）
45
37