

甘肃省白银市名校2024届高三下学期联合调研(二模)数学试卷(含答案)
展开一、选择题
1.已知集合,,则( )
A.B.C.D.
2.已知,则z在复平面内对应的点位于( )
A.第一象限B.第二象限C.第三象限D.第四象限
3.已知等比数列的各项均为正数,若,,则( )
A.4B.C.D.
4.函数的图象大致为( )
A. B.
C.D.
5.已知直线l交抛物线于M,N两点,且MN的中点为,则直线l的斜率为( )
A.B.C.D.
6.某班级举行“变废为宝”手工活动,某学生用扇形纸壳裁成扇环(如图1)后,制成了简易笔筒(如图2)的侧面,在它的轴截面ABCD中,,,则原扇形纸壳中扇形的圆心角为( )
A.B.C.D.
7.已知椭圆,,为两个焦点,P为椭圆C上一点,若,则的面积为( )
A.2B.3C.4D.6
8.在正三棱锥中,的边长为6,侧棱长为8,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
A.B.C.D.
二、多项选择题
9.已知函数的最小正周期为π,则( )
A.
B.
C.图象的一个对称中心为
D.在上单调递增
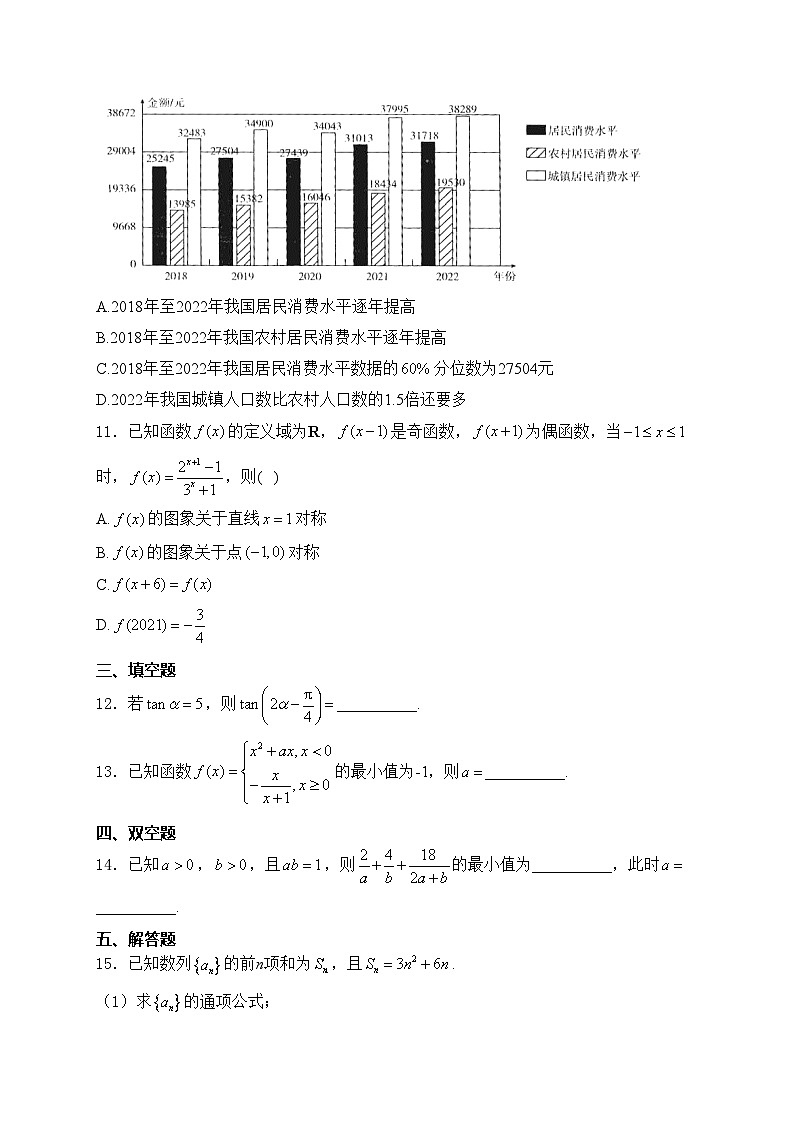
10.国家统计局发布的2018年至2022年我国居民消费水平情况如图所示,则下列说法正确的是()( )
A.2018年至2022年我国居民消费水平逐年提高
B.2018年至2022年我国农村居民消费水平逐年提高
C.2018年至2022年我国居民消费水平数据的分位数为27504元
D.2022年我国城镇人口数比农村人口数的1.5倍还要多
11.已知函数的定义域为R,是奇函数,为偶函数,当时,,则( )
A.的图象关于直线对称
B.的图象关于点对称
C.
D.
三、填空题
12.若,则__________.
13.已知函数的最小值为-1,则__________.
四、双空题
14.已知,,且,则的最小值为__________,此时__________.
五、解答题
15.已知数列的前n项和为,且.
(1)求的通项公式;
(2)设,求数列的前n项和.
16.已知函数.
(1)若,求曲线在处的切线方程;
(2)若,恒成立,求实数a的取值范围.
17.如图,在四棱锥中,四边形ABCD是等腰梯形,,,,.
(1)证明:平面平面ABCD.
(2)若,且,求二面角的正弦值.
18.卫生纸主要供人们生活日常卫生之用,是人民群众生活中不可缺少的纸种之一.某品牌卫生纸生产厂家为保证产品的质量,现从甲、乙两条生产线生产的产品中各随机抽取500件进行品质鉴定,并将统计结果整理如下:
(1)根据的独立性检验,能否认为产品的品质与生产线有关?
(2)用频率近似概率,从甲、乙两条生产线生产的产品中各随机抽取2件进行详细检测,记抽取的产品中优等品的件数为X,求随机变量X的分布列与数学期望.
附:,其中.
19.已知P,Q分别为双曲线的左、右支上的点,C的右焦点为F,O为坐标原点.
(1)若P,Q,F三点共线,且的面积为,求直线PQ的方程.
(2)若直线PQ与圆相切,试判断是否为定值.若是,求出该定值;若不是,请说明理由.
参考答案
1.答案:D
解析:.
2.答案:B
解析:因为,所以z在复平面内对应的点位于第二象限.
3.答案:B
解析:因为,且各项均为正数,所以.
4.答案:B
解析:由题易知为偶函数,排除A选项;当时,,,所以,排除C,D选项.
5.答案:C
解析:易知直线l的斜率存在,设直线l的斜率为k,,,则,两式相减得,整理得.因为MN的中点为,所以,即直线l的斜率为.
6.答案:B
解析:延长CB,DA交于点O,设圆台上、下个底面的圆心分别为,.连接,
设,,.因为,所以,
则.设所求圆心角为,则,所以.
7.答案:C
解析:由,解得,.因为,,所以,.
8.答案:A
解析:如图,取AD的中点F,连接CF,EF.因为E,F分别为AB,AD的中点,所以,所以异面直线CE与BD所成的角为.因为,,所以.因为E为AB的中点,所以.在中,因为,,所以,故异面直线CE与BD所成角的余弦值为.
9.答案:ACD
解析:,因为的最小正周期为π,所以,所以,故A正确,B不正确;因为,所以,所以是图象的一个对称中心,故C正确;令,,得,,当时,,所以D正确.
10.答案:BD
解析:2019年的居民消费水平比2020年的居民消费水平高,A错误.2018年至2022年我国农村居民消费水平逐年提高,B正确.2018年至2022年我国居民消费水平数据从小到大排序为25245,27439,27504,31013,31718,,2018年至2022年我国居民消费水平数据的分位数为元,C错误.设我国农村人口数为x,城镇人口数为y,则,化简得,所以2022年我国城镇人口数比农村人口数的1.5倍还要多,正确.
11.答案:ABD
解析:是奇函数,的图象关于点对称,即.为偶函数,的图象关于直线对称,即,故A,B正确.,,,即函数的周期为8,,故C不正确,D正确.
12.答案:
解析:因为,所以,所以.
13.答案:2
解析:当时,.因为的最小值为-1,所以函数在上取得最小值-1,则,解得.
14.答案:12;1或
解析:因为,当且仅当,即或时,等号成立,所以的最小值为12.
15、
(1)答案:
解析:当时,,当时,.
符合,所以数列的通项公式为.
(2)答案:
解析:,则.
16、
(1)答案:
解析:若,则,所以.
因为,
所以,所以所求切线方程为,即.
(2)答案:
解析:因为,
所以在上单调递减,在上单调递增,
所以.
因为当时,恒成立,
所以,所以,故实数a的取值范围是.
17、
(1)答案:证明见解析
解析:证明:如图1,在等腰梯形ABCD中,作于E,于F.
,所以,,
所以,则.
因为,平面,平面,,所以平面.
因为平面ABCD,所以平面平面ABCD.
(2)答案:
解析:由(1)得平面PBD,所以.
因为,,所以平面.
以点D为原点建立如图2所示的空间直角坐标系,则,,,,,,.设平面PAB的法向量为,则有令,可取.平面的一个法向量.设二面角的平面角为,则,,故二面角的正弦值为.
18.答案:(1)不能认为产品的品质与生产线有关
(2)分布列见解析,
解析:(1)补充列联表如下:
零假设:产品的品质与生产线无关,
根据列联表中的数据,经计算得到,
根据的独立性检验,推断成立,即不能认为产品的品质与生产线有关.
(2)由样本数据可知甲、乙两条生产线生产的产品中优等品的频率分别为,.
所以估计从甲、乙两生产线生产的产品中各随机抽取1件产品,其为优等品的概率分别为,.
X的所有可能值为0,1,2,3,4,
;
;
;
;
.
所以X的分布列为
所以.
19.答案:(1)
(2)为定值,定值为
解析:(1)易知,因为P,Q,F三点共线,所以设直线PQ的方程为,,,
联立方程组,得,
则,,且,所以,
所以.
又原点O到直线PQ的距离,
所以,
则,
解得或(舍去),所以直线PQ的方程为.
(2)设直线PQ的方程为,因为直线PQ与圆相切,
所以,即.联立方程组得,设,,则,.因为,,
所以,
所以,所以,所以,故为定值,且定值为.
合格品
优等品
甲生产线
250
250
乙生产线
300
200
0.050
0.010
0.001
3.841
6.635
10.828
合格品
优等品
总计
甲生产线
250
250
500
乙生产线
300
200
500
总计
550
450
1000
X
0
1
2
3
4
P
甘肃省白银市靖远县2024届高三下学期第三次联考(三模)数学试卷(PDF版附答案): 这是一份甘肃省白银市靖远县2024届高三下学期第三次联考(三模)数学试卷(PDF版附答案),共9页。
甘肃省白银市名校2023-2024学年高三下学期联合检测数学试题及详细答案: 这是一份甘肃省白银市名校2023-2024学年高三下学期联合检测数学试题及详细答案,共19页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2024白银名校高三下学期联合调研试题(二模)数学PDF版含解析: 这是一份2024白银名校高三下学期联合调研试题(二模)数学PDF版含解析,共7页。












