

广西防城港市上思县2023-2024学年六年级下学期数学学习成果监测(一)
展开
这是一份广西防城港市上思县2023-2024学年六年级下学期数学学习成果监测(一),共15页。试卷主要包含了填空,判断,选择,计算,统计,解决问题等内容,欢迎下载使用。
一、填空。(第10题2分,其余每空1分,共22分)
1.扇形统计图中,每个扇形分别表示各部分数量占总数量的 ,可以清楚地表示 与 之间的关系。
2.一个圆柱的底面周长是6.28分米,高5分米,它的侧面积是 平方分米,表面积是 平方分米,体积是 立方分米。
3.用一张边长8分米的正方形铁皮卷成一个最大的圆柱(接头处忽略不计),这个圆柱的高是 分米,侧面积是 平方分米。
4.做一根底面直径20厘米、长50厘米的圆柱形通风管,至少需要铁皮 平方厘米。
5.一个圆锥的体积是6立方分米,底面积是6平方分米,高是 分米。
6.一个圆柱形橡皮泥,底面积是30平方厘米,高是5厘米。把它捏成等底的圆锥,圆锥高是 厘米。
7.把一根圆柱形木料截成2段圆柱,表面积增加了18平方厘米,它的底面积是 平方厘米。如果这根木料原来长2米,它的体积是 立方厘米。
8.一根圆柱形油管,内直径是2分米,油在管内的流速是4分米/秒,每秒流过的油是 立方分米。
9. 一件毛衣中各种材质含量如下图。
(1)兔毛含量占这件毛衣总量的 %。
(2) 含量最多, 含量最少。
(3)这件毛衣重400克,羊毛有 克,棉有 克,涤纶有 克。
10.一根长2米、横截面直径是4分米的圆柱形木头浮在水面上,如果正好有一半露出水面(如下图),这根木头与水面接触的面积是 平方分米。
二、判断。(5分)
11.圆柱的体积是圆锥体积的3倍。( )
12.扇形统计图中,所有百分数之和是1。( )
13.从圆锥顶点到底面任意一点的距离叫作圆锥的高。( )
14.为了反映某地区降雨量的变化情况,用扇形统计图最合适。( )
15.在同一个扇形统计图中,扇形面积越大,它所占的百分比就越大。( )
三、选择。(把正确答案的序号填在括号里)(5分)
16. 用铁皮做一个无盖的圆柱形水桶,至少要用多少铁皮,是求水桶的( )。
A.底面积 B.侧面积 C.一个底面积+侧面积
17.一个圆柱的侧面展开图正好是一个正方形,这个圆柱的高和它的( )相等。
A.底面半径B.底面直径C.底面周长
18. 一个圆柱形罐头盒,底面周长6.28分米,高1.5分米,这个圆柱形罐头盒的体积是( )立方分米。
A.4.71B.6.28C.9.42
19.一个容器上面是圆锥、下面是圆柱,圆柱高10厘米,圆锥高6厘米,容器内的液面高度是8厘米。把容器倒过来,液面高度是( )厘米。
A.10B.12C.18
20. 六年级同学在一次体能测试中的成绩统计如下:
下面图( )能表示六年级同学在这次体能测试成绩的统计结果。
A.B.C.
四、计算。(22分)
21. 直接写出得数。
22.计算下面各题。
914÷718×29 324÷[912×(518−16)]
23.计算圆柱的表面积。
24.计算下面图形的体积。
(1)
(2)
五、统计(8分)
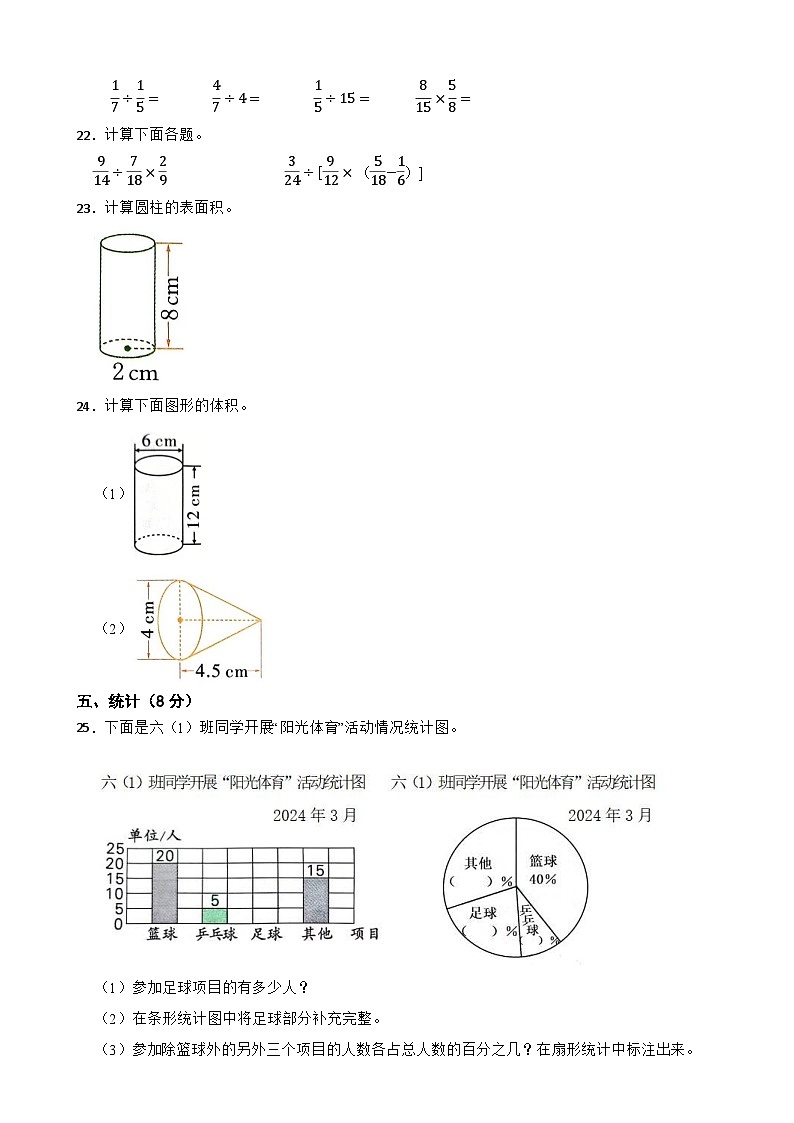
25.下面是六(1)班同学开展“阳光体育”活动情况统计图。
(1)参加足球项目的有多少人?
(2)在条形统计图中将足球部分补充完整。
(3)参加除篮球外的另外三个项目的人数各占总人数的百分之几?在扇形统计中标注出来。
六、解决问题。(38分)
26.一个圆柱形茶杯,茶杯中间有一圈隔热塑料(涂色部分),隔热塑料宽6厘米。
(1)这圈隔热塑料的面积是多少平方厘米?
(2)这个茶杯的体积是多少立方厘米?
27.一个上下都是圆锥形的沙漏,底面半径都是6厘米,高都是10厘米。
(1)在沙漏下面的圆锥中装满沙子,能装沙子多少立方厘米?
(2)将下面圆锥装满沙子的沙漏倒置,如果每分钟向下漏20立方厘米,这些沙子全部漏完,需要多少分钟?
28.一个圆锥形沙堆高3米,占地面积是18平方米。把这堆沙子铺在宽9米的路上,平均厚度5厘米,能铺多长?
29.一个草堆是由一个近似的圆锥形和一个近似的圆柱形组成(如图)。这个草堆的体积大约是多少立方米?
30.一个底面直径是10厘米的容器里装有一些水,水中浸没着一个高6厘米的圆锥形物体(完成浸没),将圆锥形物体从水中取出后,水面下降了0.8厘米,这个圆锥形物体的底面积是多少平方厘米?
31.从一张铁皮上剪下图中的涂色部分(如图),正好可以做成一个底面直径是4分米的圆柱形油桶。
(1)这个油桶的容积是多少立方分米?(铁皮厚度忽略不计)
(2)请提出一个数学问题,并解答。
答案解析部分
1.【答案】百分比;各部分数量;总数量
【知识点】扇形统计图的特点及绘制
【解析】【解答】解:扇形统计图中,每个扇形分别表示各部分数量占总数量的百分比,可以清楚地表示各部分数量与总数量之间的关系。
故答案为:百分比;各部分数量;总数量。【分析】扇形统计图能反映部分与整体的关系;根据扇形统计图的定义及特征解答即可。
2.【答案】31.4;37.68;15.7
【知识点】圆柱的侧面积、表面积;圆柱的体积(容积)
【解析】【解答】解: 侧面积:6.28×5=31.4(平方分米)
6.28÷3.14÷2=1(分米)
表面积:31.4+3.14×12×2
=31.4+6.28
=37.68(平方分米)
体积:3.14×12×5
=3.14×5
=15.7(立方分米)
故答案为:31.4;37.68;15.7。
【分析】根据圆柱的侧面积=底面周长×高,表面积=侧面积+2个底面积,体积=底面积×高,半径=周长÷π÷2,代入公式计算即可。
3.【答案】8;64
【知识点】圆柱的侧面积、表面积
【解析】【解答】解:圆柱的高:8分米
侧面积:8×8=64(平方分米)
故答案为:8;64。
【分析】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个正方形,正方形的边长等于圆柱的底面周长,也等于圆柱的高。根据圆柱的侧面积公式:S=Ch,把数据代入公式解答。
4.【答案】3140
【知识点】圆柱的侧面积、表面积
【解析】【解答】解:3.14×20×50
=3.14×1000
=3140(平方厘米)
故答案为:3140。
【分析】本题就是求底面直径为20厘米,高50厘米的圆柱的侧面积,利用圆柱的侧面积=底面周长×高即可计算。
5.【答案】3
【知识点】圆锥的体积(容积)
【解析】【解答】解:6×3÷6
=18÷6
=3(分米)
故答案为:3。
【分析】根据圆锥的体积公式可得:圆锥的高=圆锥的体积×3÷底面积,代入数据计算即可。
6.【答案】15
【知识点】圆柱与圆锥体积的关系
【解析】【解答】解:5×3=15(厘米)
故答案为:15。
【分析】体积和底面积相等的圆柱与圆锥,圆锥的高是圆柱高的3倍;据此用乘法解答。
7.【答案】9;1800
【知识点】圆柱的侧面积、表面积;圆柱的体积(容积)
【解析】【解答】解:18÷2=9(平方厘米)
2米=200厘米
9×200=1800(立方厘米)
故答案为:9;1800。
【分析】把一根圆柱形木料截成2段圆柱,表面积比原来增加了2个横截面的面积,用增加的表面积除以2就是底面积,再用底面积乘高(即木料的长)即可。
8.【答案】12.56
【知识点】圆柱的体积(容积)
【解析】【解答】解:3.14×(2÷2)2×4
=3.14×1×4
=12.56(立方分米)
故答案为:12.56。
【分析】已知一根圆柱形油管,内直径是2分米,油在管内的形状是圆柱形,油在管内的流速是4分米/秒,相当于圆柱的高;由此可利用圆柱的体积公式V=Sh即可解答。
9.【答案】(1)8
(2)羊毛;棉
(3)240;28;100
【知识点】从扇形统计图获取信息;百分数的应用--运用乘法求部分量
【解析】【解答】解:(1)1-60%-25%-7%=8%
(2)60%>25%>8%>7%
羊毛含量最多,棉含量最少。
(3)羊毛:400×60%=240(克)
棉:400×7%=28(克)
涤纶:400×25%=100(克)
故答案为:(1)8;(2)羊毛,棉;(3)240;28;100。
【分析】(1)把总量看作单位“1”,减去已知各种材质含量占的百分率;
(2)比较各含量的百分率即可
(3)根据一个数的百分之几是多少,用乘法即可解答。
10.【答案】138.16
【知识点】圆柱的侧面积、表面积
【解析】【解答】解:2米=20分米
3.14×4×20÷2+3.14×(4÷2)2
=125.6+12.56
=138.16(平方分米)
故答案为:138.16。
【分析】由题意可知,这根木头与水面接触的面积等于它的侧面积的一半加上一个底面的面积,根据圆柱的侧面积公式“S=Ch”和底面积公式“S=πr2”,代入数据计算即可。
11.【答案】错误
【知识点】圆柱与圆锥体积的关系
【解析】【解答】解:等底等高的圆柱的体积是圆锥体积的3倍,原题说法错误。
故答案为:错误。
【分析】圆柱体积=底面积×高,圆锥体积=底面积×高×13,所以等底等高的圆柱体积是圆锥体积的3倍.
12.【答案】正确
【知识点】扇形统计图的特点及绘制
【解析】【解答】解:扇形统计图中,所有百分数之和是1。说法正确。
故答案为:正确。
【分析】扇形统计图中,圆代表整体,即单位“1”,各个扇形代表部分,各部分之和等于100%。
13.【答案】错误
【知识点】圆锥的特征
【解析】【解答】解: 从圆锥的顶点到底面圆心的距离叫作圆锥的高;
故答案为:错误。
【分析】根据圆锥高的概念进行判断。
14.【答案】错误
【知识点】统计图的选择
【解析】【解答】解:为了反映某地区降雨量的变化情况,用折线统计图最合适。原说法错误。
故答案为:错误。
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此判断。
15.【答案】正确
【知识点】扇形统计图的特点及绘制
【解析】【解答】解:在同一个扇形统计图中,扇形面积越大,它所占的百分比就越大。说法正确。
故答案为:正确。
【分析】同一扇形统计图中,各部分占总体的百分比之和为1,每部分占总体的百分比等于该部分所对应的扇形,所以扇形越大,说明这一部分占总量的百分比就越大。
16.【答案】C
【知识点】圆柱的侧面积、表面积
【解析】【解答】解:用铁皮做一个无盖的圆柱形水桶,至少要用多少铁皮,是求水桶的侧面积和一个底面积的和。
故答案为:C。
【分析】圆柱的上、下底面是完全相同的两个圆,侧面是一个曲面,侧面展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高;根据题意可知,因为铁皮水桶无盖,因此计算做一个无盖的圆柱形铁皮水桶需要多少铁皮,其实就是计算水桶的侧面积和一个底面积的和。
17.【答案】C
【知识点】圆柱的展开图
【解析】【解答】解: 一个圆柱的侧面展开图正好是一个正方形,这个圆柱的高和它的底面周长相等。
故答案为:C。
【分析】根据圆柱体的特征,它的上、下底面是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形或正方形,长方形的长等于圆柱的底面周长,宽等于圆柱的高;由此解答。
18.【答案】A
【知识点】圆柱的体积(容积)
【解析】【解答】解:6.28÷3.14÷2
=2÷2
=1(分米)
3.14×12×1.5
=3.14×1.5
=4.71(立方分米)
故答案为:A。
【分析】已知底面周长,先求出半径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
19.【答案】B
【知识点】圆柱与圆锥体积的关系
【解析】【解答】解:8-6×13+6
=8-2+6
=6+6
=12(厘米)
故答案为:B。
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的13,由此可知,圆柱容器内高(6×13)厘米的水正好倒满圆锥容器,然后用圆柱容器内剩下水的高加上圆锥的高即可。据此解答即可。
20.【答案】B
【知识点】扇形统计图的特点及绘制
【解析】【解答】解:总人数:40+20+10+10=80(人)
优秀:40÷80×100%=50%
良好:20÷80×100%=25%
达标:10÷80×100%=12.5%
不合格:10÷80×100%=12.5%
能表示这次体能测试的统计结果。
故答案为:B。
【分析】结合统计表中的数据,分别计算出每个等级的人数占总人数的百分比,从而选择合适的统计图。
21.【答案】
【知识点】分数与整数相乘;分数与分数相乘;除数是整数的分数除法;除数是分数的分数除法
【解析】【分析】异分数分数的加减法计算,先通分再计算;
分数乘整数,分母不变,只把分子与整数相乘,能约分的要约分;
分数乘分数,分子与分子相乘,分母与分母相乘,能约分的要约分;
分数除法的计算,先乘除数的倒数,再根据分数乘分数的计算法则进行计算。
22.【答案】解:914÷718×29
=914×187×29
=1849
324÷[912×(518−16)]
=324÷[912×(518−318)]
=324÷[912×19]
=324÷112
=324×12
=32
【知识点】分数四则混合运算及应用
【解析】【分析】(1)先算除法,再算乘法;
(2)先算小括号里面的减法,再算中括号里面的乘法,最后算括号外面的除法。
23.【答案】解:2×3.14×2×8+3.14×22×2
=12.56×8+3.14×4×2
=100.48+25.12
=125.6(平方厘米)
圆柱的表面积是125.6平方厘米。
【知识点】圆柱的侧面积、表面积
【解析】【分析】圆柱的表面积=侧面积+底面积×2,把数据代入公式解答。
24.【答案】(1)解:3.14×(6÷2)2×12
=3.14×9×12
=28.26×12
=339.12(立方厘米)
(2)解:3.14×(4÷2)2×4.5×13
=3.14×4×1.5
=3.14×6
=18.84(立方厘米)
【知识点】圆柱的体积(容积);圆锥的体积(容积)
【解析】【分析】圆柱的体积公式V=πr2h,圆锥的体积公式V=13πr2h,将数据代入公式即可解答。
25.【答案】(1)解:20÷40%=50(人)
50-20-5-15=10(人)
答:参加足球项目的有10人。
(2)
(3)解:乒乓球:5÷50=0.1=10%
足球:10÷50=0.2=20%
其他:15÷50=0.3=30%
【知识点】扇形统计图的特点及绘制;从单式折线统计图获取信息;从扇形统计图获取信息
【解析】【分析】(1)由图可知,打篮球的有20人,占总人数的40%,据此用除法即可求出参加“阳光体育活动”的总人数,再用总人数减去篮球、乒乓球、其他的人数,就是参加足球项目的人数;
(2)已知参加足球项目的有10人,据此完成条形统计图;
(3)分别用部分量除以总量,求出占的百分率,据此求出乒乓球、足球和其他各占总人数的百分之几,再完成统计图即可。
26.【答案】(1)解:3.14×8×6
=25.12×6
=150.72(平方厘米)
答: 这圈隔热塑料的面积是150.72平方厘米。
(2)8÷2=4(厘米)
3.14×42×15
=3.14×16×15
=50.24×15
=753.6(立方厘米)
答:这个茶杯的体积是753.6立方厘米。
【知识点】圆柱的侧面积、表面积;圆柱的体积(容积)
【解析】【分析】(1)根据圆柱的侧面积公式:S=Ch, 隔热塑料宽 6厘米,把数据代入公式解答;
(2)根据圆柱的体积公式:V=Sh,把数据代入公式解答。
27.【答案】(1)解:3.14×62×10×13
=3.14×36×10×13
=3.14×120
=376.8(立方厘米)
答:能装沙子376.8立方厘米。
(2)解:376.8÷20=18.84(分)
答:这些沙子全部漏完,需要18.84分钟。
【知识点】除数是整数的小数除法;圆锥的体积(容积)
【解析】【分析】(1)圆锥体积公式:V=13Sh,代入数据解答即可;
(2)根据“包含”除法的意义,用沙漏内沙子的体积除以每分钟漏掉的体积即可。
28.【答案】解:5厘米=0.05米
13×18×3÷(9×0.05)
=18÷0.45
=40(米)
答:能铺40米长。
【知识点】圆锥的体积(容积);体积的等积变形;长方体、正方体的容积
【解析】【分析】根据圆锥的体积公式:V=13Sh,计算出这堆沙的体积,把这堆沙平铺在路面上,只是形状改变了,沙的体积没变,由长方体的公式:V=Sh,用体积除以底面积就是铺的长度;由此解答。
29.【答案】解:3.14×(3÷2)2×1+3.14×(3÷2)2×2×13
=3.14×2.25+3.14×2.25×2×13
=7.065+4.71
=11.775(立方米)
答:这个草堆的体积大约是11.775立方米。
【知识点】圆柱的体积(容积);圆锥的体积(容积);组合体的体积的巧算
【解析】【分析】根据圆锥的体积公式V=13πr2h和圆柱的体积公式V=πr2h,把数据代入公式求出它们的体积后求和即可。
30.【答案】解:10÷2=5(厘米)
3.14×52×0.8
=3.14×25×0.8
=62.8(立方厘米)
62.8×3÷6
=188.4÷6
=31.4(平方厘米)
答:这个铅锤的底面积是31.4平方厘米。
【知识点】圆柱的体积(容积);圆锥的体积(容积)
【解析】【分析】当把铅锤取出圆柱形容器中下降部分水的体积等于铅锤的体积,根据圆柱的体积公式:V=πr2h,把数据代入公式求出圆锥的体积,进而求出圆锥的底面积。
31.【答案】(1)解:4÷2=2(分米)
3.14×22×4
=3.14×4×4
=50.24(立方分米)
答:这个油桶的容积是50.24立方分米。
(2)解:提问:这个圆柱的底面积是多少平方分米?
3.14×(4÷2)2
=3.14×4
=12.56(平方分米)
答:这个圆柱的底面积是12.56平方分米。
【知识点】圆柱的侧面积、表面积;圆柱的体积(容积)
【解析】【分析】(1)从图中可以看出,做成的圆柱形油桶的底面直径和高都是4分米; 根据圆柱的容积公式:V=πr2h,把数据代入公式解答;
(2)提出合理问题并解答即可。等级
优秀
良好
达标
不合格
人数
40
20
10
10
38+14=
15−16=
79×27=
28×57=
17÷15=
47÷4=
15÷15=
815×58=
38+14=58
15−16=130
79×27=21
28×57=20
17÷15=57
47÷4=17
15÷15=175
815×58=13
相关试卷
这是一份广西防城港市上思县2023-2024学年四年级下学期数学学习成果监测(一),共14页。试卷主要包含了填空,判断,选择,实践操作,解决问题等内容,欢迎下载使用。
这是一份广西防城港市上思县2023-2024学年五年级下学期数学学习成果监测(一),共13页。试卷主要包含了填空,判断,选择题,解方程,求x的值,列方程解决问题,统计等内容,欢迎下载使用。
这是一份广西防城港市上思县2023-2024学年三年级下学期数学学习成果监测(一),共12页。试卷主要包含了填空题,判断题,选择题,计算题,按要求完成下面各题,解决问题等内容,欢迎下载使用。










