2024年中考数学二轮题型突破练习题型9 二次函数综合题 类型6 二次函数与等腰三角形有关的问题（专题训练）（2份打包，原卷版+教师版）

这是一份2024年中考数学二轮题型突破练习题型9 二次函数综合题 类型6 二次函数与等腰三角形有关的问题（专题训练）（2份打包，原卷版+教师版），文件包含2024年中考数学二轮题型突破练习题型9二次函数综合题类型6二次函数与等腰三角形有关的问题专题训练原卷版doc、2024年中考数学二轮题型突破练习题型9二次函数综合题类型6二次函数与等腰三角形有关的问题专题训练教师版doc等2份试卷配套教学资源，其中试卷共61页， 欢迎下载使用。
(1)求该抛物线的表达式；
(2)点 SKIPIF 1 < 0 是直线 SKIPIF 1 < 0 下方抛物线上一动点，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的最大值及此时点 SKIPIF 1 < 0 的坐标；
(3)在（2）的条件下，将该抛物线向右平移 SKIPIF 1 < 0 个单位，点 SKIPIF 1 < 0 为点 SKIPIF 1 < 0 的对应点，平移后的抛物线与 SKIPIF 1 < 0 轴交于点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 为平移后的抛物线的对称轴上任意一点．写出所有使得以 SKIPIF 1 < 0 为腰的 SKIPIF 1 < 0 是等腰三角形的点 SKIPIF 1 < 0 的坐标，并把求其中一个点 SKIPIF 1 < 0 的坐标的过程写出来．
【答案】(1) SKIPIF 1 < 0 ；(2) SKIPIF 1 < 0 取得最大值为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；(3) SKIPIF 1 < 0 点的坐标为 SKIPIF 1 < 0 或 SKIPIF 1 < 0 或 SKIPIF 1 < 0
【分析】（1）待定系数法求二次函数解析式即可求解；
（2）直线 SKIPIF 1 < 0 的解析式为 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 ，交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，进而根据二次函数的性质即可求解；
（3）根据平移的性质得出 SKIPIF 1 < 0 ，对称轴为直线 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 向右平移5个单位得到 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，勾股定理分别表示出 SKIPIF 1 < 0 ，进而分类讨论即可求解．
【详解】（1）解：将点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．代入 SKIPIF 1 < 0 得，
SKIPIF 1 < 0
解得： SKIPIF 1 < 0 ，
∴抛物线解析式为： SKIPIF 1 < 0 ，
（2）∵ SKIPIF 1 < 0 与 SKIPIF 1 < 0 轴交于点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0
解得： SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ,
∵ SKIPIF 1 < 0 ．
设直线 SKIPIF 1 < 0 的解析式为 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
解得： SKIPIF 1 < 0
∴直线 SKIPIF 1 < 0 的解析式为 SKIPIF 1 < 0 ，
如图所示，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 ，交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，

设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得最大值为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ；
（3）∵抛物线 SKIPIF 1 < 0 SKIPIF 1 < 0
将该抛物线向右平移 SKIPIF 1 < 0 个单位，得到 SKIPIF 1 < 0 ，对称轴为直线 SKIPIF 1 < 0 ，
点 SKIPIF 1 < 0 向右平移5个单位得到 SKIPIF 1 < 0
∵平移后的抛物线与 SKIPIF 1 < 0 轴交于点 SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0
∵ SKIPIF 1 < 0 为平移后的抛物线的对称轴上任意一点．
则 SKIPIF 1 < 0 点的横坐标为 SKIPIF 1 < 0 ，
设 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 SKIPIF 1 < 0 SKIPIF 1 < 0 ，
解得： SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 SKIPIF 1 < 0 SKIPIF 1 < 0 ，
解得： SKIPIF 1 < 0
综上所述， SKIPIF 1 < 0 点的坐标为 SKIPIF 1 < 0 或 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ．
【点睛】本题考查了二次函数综合问题，解直角三角形，待定系数法求解析式，二次函数的平移，线段周长问题，特殊三角形问题，熟练掌握二次函数的性质是解题的关键．
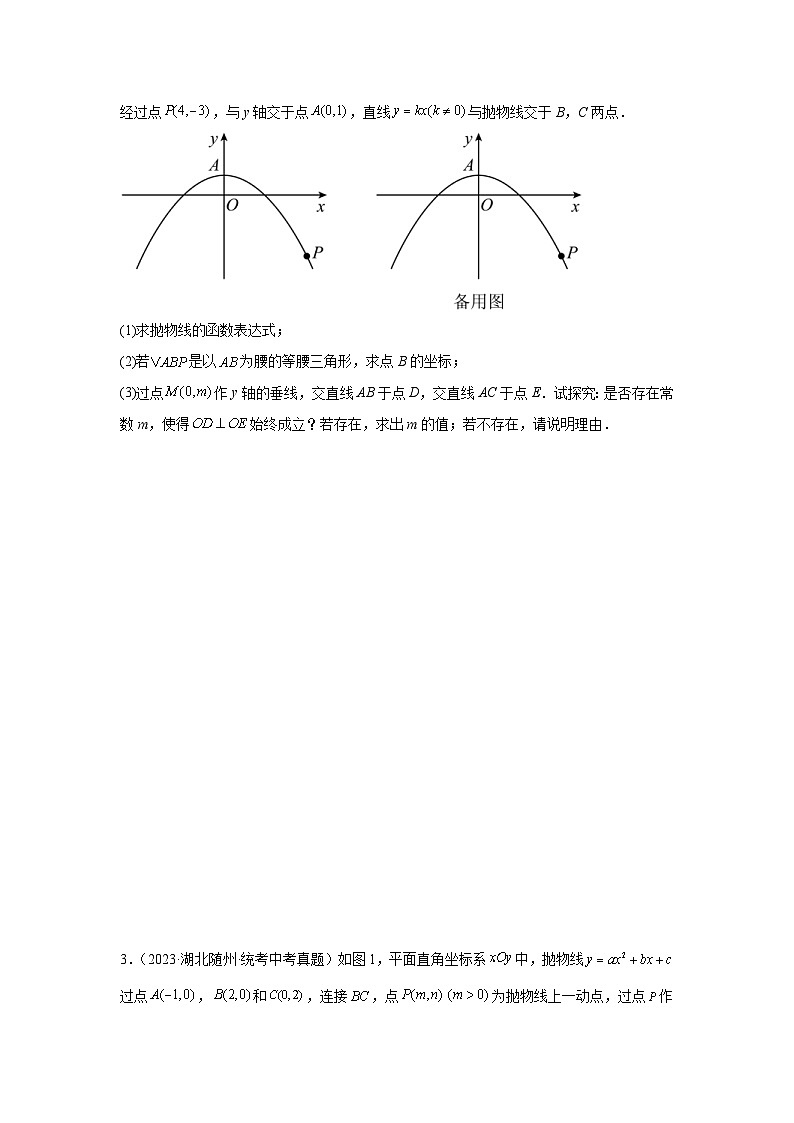
2．（2023·四川成都·统考中考真题）如图，在平面直角坐标系 SKIPIF 1 < 0 中，已知抛物线 SKIPIF 1 < 0 经过点 SKIPIF 1 < 0 ，与y轴交于点 SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 与抛物线交于B，C两点．

(1)求抛物线的函数表达式；
(2)若 SKIPIF 1 < 0 是以 SKIPIF 1 < 0 为腰的等腰三角形，求点B的坐标；
(3)过点 SKIPIF 1 < 0 作y轴的垂线，交直线AB于点D，交直线AC于点E．试探究：是否存在常数m，使得 SKIPIF 1 < 0 始终成立？若存在，求出m的值；若不存在，请说明理由．
【答案】(1) SKIPIF 1 < 0 ；(2)点B的坐标为 SKIPIF 1 < 0 或 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ；(3)存在，m的值为2或 SKIPIF 1 < 0
【分析】（1）利用待定系数法求解即可；
（2）设 SKIPIF 1 < 0 ，分 SKIPIF 1 < 0 和 SKIPIF 1 < 0 两种情况，分别根据等腰三角形性质和两点坐标距离公式列方程求解即可；
（3）先根据题意画出图形，设抛物线 SKIPIF 1 < 0 与直线 SKIPIF 1 < 0 的交点坐标为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，联立抛物线和直线解析式，根据根与系数关系得到 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，利用待定系数法分别求得直线 SKIPIF 1 < 0 、 SKIPIF 1 < 0 的表达式为得到 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，过E作 SKIPIF 1 < 0 轴于Q，过D作 SKIPIF 1 < 0 轴于N，证明 SKIPIF 1 < 0 得到 SKIPIF 1 < 0 ，整理可得到 SKIPIF 1 < 0 ，进而求解即可．
【详解】（1）解：∵抛物线 SKIPIF 1 < 0 经过点 SKIPIF 1 < 0 ，与y轴交于点 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
∴抛物线的函数表达式为 SKIPIF 1 < 0 ；
（2）解：设 SKIPIF 1 < 0 ，
根据题意， SKIPIF 1 < 0 是以 SKIPIF 1 < 0 为腰的等腰三角形，有两种情况：
当 SKIPIF 1 < 0 时，点B和点P关于y轴对称，

∵ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 时，则 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
整理，得 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
综上，满足题意的点B的坐标为 SKIPIF 1 < 0 或 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ；
（3）解：存在常数m，使得 SKIPIF 1 < 0 ．
根据题意，画出图形如下图，

设抛物线 SKIPIF 1 < 0 与直线 SKIPIF 1 < 0 的交点坐标为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
由 SKIPIF 1 < 0 得 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；
设直线 SKIPIF 1 < 0 的表达式为 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
∴直线 SKIPIF 1 < 0 的表达式为 SKIPIF 1 < 0 ，
令 SKIPIF 1 < 0 ，由 SKIPIF 1 < 0 得 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
同理，可得直线 SKIPIF 1 < 0 的表达式为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
过E作 SKIPIF 1 < 0 轴于Q，过D作 SKIPIF 1 < 0 轴于N，
则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，
整理，得 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，
将 SKIPIF 1 < 0 ， SKIPIF 1 < 0 代入，得 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
综上，存在常数m，使得 SKIPIF 1 < 0 ，m的值为2或 SKIPIF 1 < 0 ．
【点睛】本题是二次函数的综合题，主要考查了待定系数法求函数的解析式、等腰三角形的性质、一元二次方程根与系数关系、相似三角形的判定与性质、解一元二次方程、坐标与图形等知识，综合性强，难度较大，熟练掌握相关知识的联系与运用，添加辅助线构造相似三角形，并利用数形结合和分类讨论思想解决问题是解答的关键．
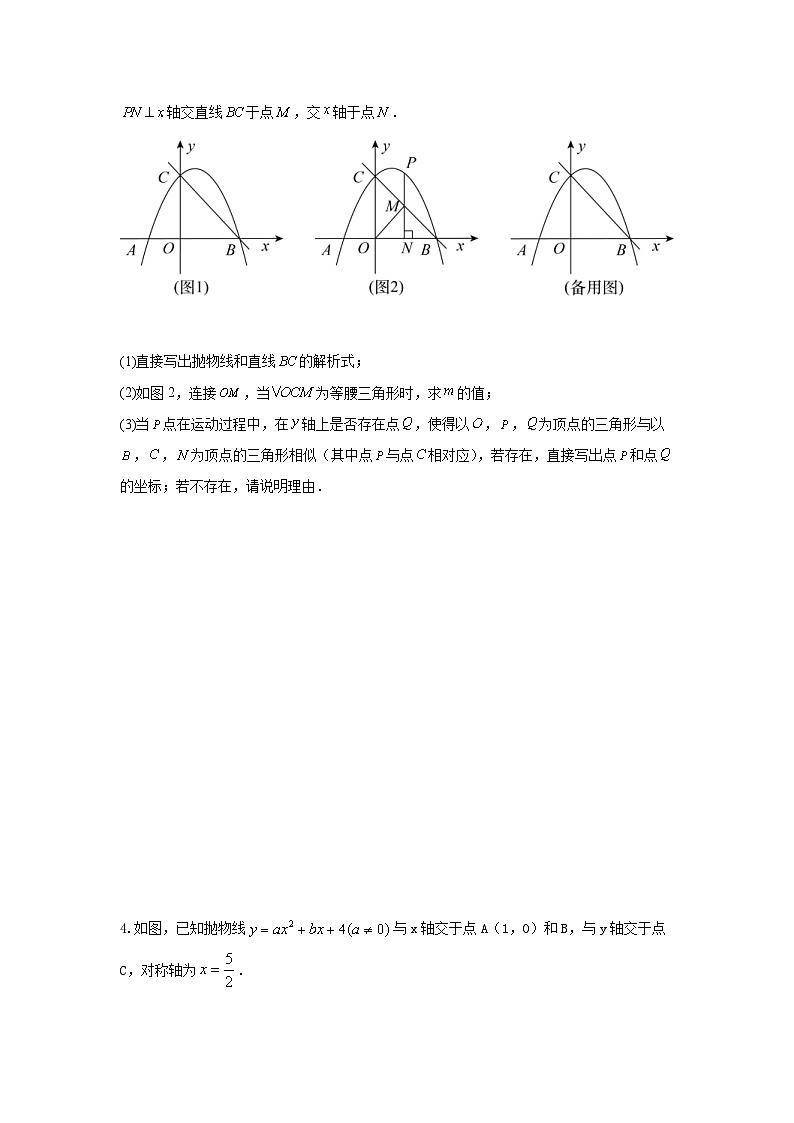
3．（2023·湖北随州·统考中考真题）如图1，平面直角坐标系 SKIPIF 1 < 0 中，抛物线 SKIPIF 1 < 0 过点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 SKIPIF 1 < 0 为抛物线上一动点，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 轴交直线 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，交 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 ．

(1)直接写出抛物线和直线 SKIPIF 1 < 0 的解析式；
(2)如图2，连接 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 为等腰三角形时，求 SKIPIF 1 < 0 的值；
(3)当 SKIPIF 1 < 0 点在运动过程中，在 SKIPIF 1 < 0 轴上是否存在点 SKIPIF 1 < 0 ，使得以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 为顶点的三角形与以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 为顶点的三角形相似（其中点 SKIPIF 1 < 0 与点 SKIPIF 1 < 0 相对应），若存在，直接写出点 SKIPIF 1 < 0 和点 SKIPIF 1 < 0 的坐标；若不存在，请说明理由．
【答案】(1)抛物线： SKIPIF 1 < 0 ；直线 SKIPIF 1 < 0 ： SKIPIF 1 < 0 ；(2) SKIPIF 1 < 0 或 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ；(3) SKIPIF 1 < 0 ， SKIPIF 1 < 0 或 SKIPIF 1 < 0 ， SKIPIF 1 < 0 或 SKIPIF 1 < 0 ， SKIPIF 1 < 0
【分析】（1）由题得抛物线的解析式为 SKIPIF 1 < 0 ，将点 SKIPIF 1 < 0 代入求 SKIPIF 1 < 0 ，进而得抛物线的解析式；设直线 SKIPIF 1 < 0 的解析式为 SKIPIF 1 < 0 ，将点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的坐标代入求 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，进而得直线 SKIPIF 1 < 0 的解析式．
（2）由题得 SKIPIF 1 < 0 ，分别求出 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，对等腰 SKIPIF 1 < 0 中相等的边进行分类讨论，进而列方程求解；
（3）对点 SKIPIF 1 < 0 在点 SKIPIF 1 < 0 左侧或右侧进行分类讨论，设法表示出各线段的长度，利用相似三角形的相似比求解 SKIPIF 1 < 0 ，进而可得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的坐标．
【详解】（1）解： SKIPIF 1 < 0 抛物线过点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 抛物线的表达式为 SKIPIF 1 < 0 ，
将点 SKIPIF 1 < 0 代入上式，得 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 SKIPIF 1 < 0 ．
SKIPIF 1 < 0 抛物线的表达式为 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ．
设直线 SKIPIF 1 < 0 的表达式为 SKIPIF 1 < 0 ，
将点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 代入上式，
得 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 ．
SKIPIF 1 < 0 直线 SKIPIF 1 < 0 的表达式为 SKIPIF 1 < 0 ．
（2）解： SKIPIF 1 < 0 点 SKIPIF 1 < 0 在直线 SKIPIF 1 < 0 上，且 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 点 SKIPIF 1 < 0 的坐标为 SKIPIF 1 < 0 ．
SKIPIF 1 < 0 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
当 SKIPIF 1 < 0 为等腰三角形时，
①若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 ．
②若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 （舍去）．
③若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 （舍去）或 SKIPIF 1 < 0 ．
综上， SKIPIF 1 < 0 或 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ．
（3）解： SKIPIF 1 < 0 点 SKIPIF 1 < 0 与点 SKIPIF 1 < 0 相对应，
SKIPIF 1 < 0 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ．
①若点 SKIPIF 1 < 0 在点 SKIPIF 1 < 0 左侧，
则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
当 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 时，
直线 SKIPIF 1 < 0 的表达式为 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 （舍去）．
SKIPIF 1 < 0 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ．
SKIPIF 1 < 0 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 ．
SKIPIF 1 < 0 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
当 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 时，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 （舍去）或 SKIPIF 1 < 0 （舍去）．
②若点 SKIPIF 1 < 0 在点 SKIPIF 1 < 0 右侧，
则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
当 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 时，
直线 SKIPIF 1 < 0 的表达式为 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 （舍去），
SKIPIF 1 < 0 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 ．
SKIPIF 1 < 0 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
当 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 时，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
SKIPIF 1 < 0 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 （舍去）．
SKIPIF 1 < 0 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
综上， SKIPIF 1 < 0 ， SKIPIF 1 < 0 或 SKIPIF 1 < 0 ， SKIPIF 1 < 0 或 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
【点睛】本题是二次函数的综合应用，考查了待定系数法求函数解析式，等腰三角形的性质与判定，平面直角坐标系中两点距离的算法，相似三角形的性质与判定等，熟练掌握相关知识是解题的关键．
4.如图，已知抛物线 SKIPIF 1 < 0 与x轴交于点A（1，0）和B，与y轴交于点C，对称轴为 SKIPIF 1 < 0 ．
（1）求抛物线的解析式；
（2）如图1，若点P是线段BC上的一个动点（不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，连接OQ．当线段PQ长度最大时，判断四边形OCPQ的形状并说明理由．
（3）如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且 SKIPIF 1 < 0 ．在y轴上是否存在点F，使得 SKIPIF 1 < 0 为等腰三角形？若存在，求点F的坐标；若不存在，请说明理由．
【答案】（1） SKIPIF 1 < 0 ；（2）四边形OCPQ是平行四边形，理由见详解；（3）（0， SKIPIF 1 < 0 ）或（0，1）或（0，-1）
【分析】
（1）设抛物线 SKIPIF 1 < 0 ，根据待定系数法，即可求解；
（2）先求出直线BC的解析式为：y=-x+4，设P（x，-x+4），则Q（x， SKIPIF 1 < 0 ），（0≤x≤4），得到PQ = SKIPIF 1 < 0 ，从而求出线段PQ长度最大值，进而即可得到结论；
（3）过点Q作QM⊥y轴，过点Q作QN∥y轴，过点E作EN∥x轴，交于点N，推出 SKIPIF 1 < 0 ，从而得 SKIPIF 1 < 0 ，进而求出E（5，4），设F（0，y），分三种情况讨论，即可求解．
【详解】
解：（1）∵抛物线 SKIPIF 1 < 0 与x轴交于点A（1，0）和B，与y轴交于点C，对称轴为直线 SKIPIF 1 < 0 ，
∴B（4，0），C（0，4），
设抛物线 SKIPIF 1 < 0 ，把C（0，4）代入得： SKIPIF 1 < 0 ，解得：a=1，
∴抛物线的解析式为： SKIPIF 1 < 0 ；
（2）∵B（4，0），C（0，4），
∴直线BC的解析式为：y=-x+4，
设P（x，-x+4），则Q（x， SKIPIF 1 < 0 ），（0≤x≤4），
∴PQ=-x+4-( SKIPIF 1 < 0 )= SKIPIF 1 < 0 = SKIPIF 1 < 0 ，
∴当x=2时，线段PQ长度最大=4，
∴此时，PQ=CO，
又∵PQ∥CO，
∴四边形OCPQ是平行四边形；
（3）过点Q作QM⊥y轴，过点Q作QN∥y轴，过点E作EN∥x轴，交于点N，
由（2）得：Q（2，-2），
∵D是OC的中点，
∴D（0，2），
∵QN∥y轴，
∴ SKIPIF 1 < 0 ，
又∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，即： SKIPIF 1 < 0 ，
设E（x， SKIPIF 1 < 0 ），则 SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 ， SKIPIF 1 < 0 （舍去），
∴E（5，4），
设F（0，y），则 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
①当BF=EF时， SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 ，
②当BF=BE时， SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
③当EF=BE时， SKIPIF 1 < 0 ，无解，
综上所述：点F的坐标为：（0， SKIPIF 1 < 0 ）或（0，1）或（0，-1）．
．
【点睛】
本题主要考查二次函数与平面几何的综合，掌握二次函数的性质以及图像上点的坐标特征，添加辅助线，构造直角三角形，是解题的关键．
5.如图，抛物线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 轴交于A(-1，0)，B(4，0)，与 SKIPIF 1 < 0 轴交于点C．连接AC，BC，点P在抛物线上运动．
(1)求抛物线的表达式；
(2)如图①，若点P在第四象限，点Q在PA的延长线上，当∠CAQ=∠CBA SKIPIF 1 < 0 45°时，求点P的坐标；
(3)如图②，若点P在第一象限，直线AP交BC于点F，过点P作 SKIPIF 1 < 0 轴的垂线交BC于点H，当△PFH为等腰三角形时，求线段PH的长．
【答案】（1） SKIPIF 1 < 0 ；（2）（6，-7）；（3）PH= SKIPIF 1 < 0 或1.5或 SKIPIF 1 < 0
【分析】
（1）根据待定系数法解答即可；
（2）求得点C的坐标后先利用勾股定理的逆定理判断∠ACB=90°，继而可得∠ACO=∠CBA，在x轴上取点E（2，0），连接CE，易得△OCE是等腰直角三角形，可得∠OCE=45°，进一步可推出∠ACE=∠CAQ，可得CE∥PQ，然后利用待定系数法分别求出直线CE与PQ的解析式，再与抛物线的解析式联立方程组求解即可；
（3）设直线AP交y轴于点G，如图，由题意可得若△PFH为等腰三角形，则△CFG也为等腰三角形，设G（0，m），求出直线AF和直线BC的解析式后，再解方程组求出点F的坐标，然后分三种情况求出m的值，再求出直线AP的解析式，进而可求出点P的坐标，于是问题可求解．
【详解】
解：（1）把A(-1，0)，B(4，0)代入 SKIPIF 1 < 0 ，得
SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 ，
∴抛物线的解析式是 SKIPIF 1 < 0 ；
（2）令x=0，则y=2，即C（0，2），
∵ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，AB2=25，
∴ SKIPIF 1 < 0 ，
∴∠ACB=90°，
∵∠ACO+∠CAO=∠CBA+∠CAO=90°，
∴∠ACO=∠CBA，
在x轴上取点E（2，0），连接CE，如图，
则CE=OE=2，
∴∠OCE=45°，
∴∠ACE=∠ACO+45°=∠CBA+45°=∠CAQ，
∴CE∥PQ，
∵C（0，2），E（2，0），
∴直线CE的解析式为y=-x+2，
设直线PQ的解析式为y=-x+n，把点A（-1，0）代入，可得n=-1，
∴直线PQ的解析式为y=-x-1，
解方程组 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
∴点P的坐标是（6，-7）；
（3）设直线AP交y轴于点G，如图，
∵PH∥y轴，
∴∠PHC=∠OCB，∠FPH=∠CGF，
∴若△PFH为等腰三角形，则△CFG也为等腰三角形，
∵C（0，2），B（4，0），
∴直线BC的解析式为 SKIPIF 1 < 0 ，
设G（0，m），∵A（-1，0），
∴直线AF的解析式为y=mx+m，
解方程组 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，
∴点F的坐标是 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
当CG=CF时， SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 （舍去负值），
此时直线AF的解析式为y= SKIPIF 1 < 0 x+ SKIPIF 1 < 0 ，
解方程组 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
∴点P的坐标是（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ），此时点H的坐标是（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ），
∴PH= SKIPIF 1 < 0 ；
当FG=FC时， SKIPIF 1 < 0 ，解得m= SKIPIF 1 < 0 或m= SKIPIF 1 < 0 （舍）或m=2（舍），
此时直线AF的解析式为y= SKIPIF 1 < 0 x+ SKIPIF 1 < 0 ，
解方程组 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
∴点P的坐标是（3，2），此时点H的坐标是（3， SKIPIF 1 < 0 ），
∴PH=2- SKIPIF 1 < 0 =1.5；
当GF=GC时， SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 或m=2（舍去），
此时直线AF的解析式为y= SKIPIF 1 < 0 x+ SKIPIF 1 < 0 ，
解方程组 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
∴点P的坐标是（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ），此时点H的坐标是（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ），
∴PH= SKIPIF 1 < 0 ；
综上，PH= SKIPIF 1 < 0 或1.5或 SKIPIF 1 < 0 ．
【点睛】
本题是二次函数的综合题，主要考查了待定系数法求二次函数的解析式、二次函数图象上点的坐标特征、直线与抛物线的交点以及等腰三角形的判定和性质等知识，具有相当的难度，熟练掌握二次函数的图象和性质、灵活应用数形结合的思想是解题的关键．
6.如图，已知二次函数 SKIPIF 1 < 0 的图象经过点 SKIPIF 1 < 0 且与 SKIPIF 1 < 0 轴交于原点及点 SKIPIF 1 < 0 ．
（1）求二次函数的表达式；
（2）求顶点 SKIPIF 1 < 0 的坐标及直线 SKIPIF 1 < 0 的表达式；
（3）判断 SKIPIF 1 < 0 的形状，试说明理由；
（4）若点 SKIPIF 1 < 0 为 SKIPIF 1 < 0 上的动点，且 SKIPIF 1 < 0 的半径为 SKIPIF 1 < 0 ，一动点 SKIPIF 1 < 0 从点 SKIPIF 1 < 0 出发，以每秒2个单位长度的速度沿线段 SKIPIF 1 < 0 匀速运动到点 SKIPIF 1 < 0 ，再以每秒1个单位长度的速度沿线段 SKIPIF 1 < 0 匀速运动到点 SKIPIF 1 < 0 后停止运动，求点 SKIPIF 1 < 0 的运动时间 SKIPIF 1 < 0 的最小值．
【答案】（1） SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；（3）等腰直角三角形，理由见解析；（4） SKIPIF 1 < 0
【分析】
（1）根据已知条件，运用待定系数法直接列方程组求解即可；
（2）根据（1）中二次函数解析式，直接利用顶点坐标公式计算即可，再根据点A、B坐标求出AB解析式即可；
（3）根据二次函数对称性可知 SKIPIF 1 < 0 为等腰三角形，再根据O、A、B三点坐标，求出三条线段的长，利用勾股定理验证即可；
（4）根据题意可知动点 SKIPIF 1 < 0 的运动时间为 SKIPIF 1 < 0 ，在 SKIPIF 1 < 0 上取点 SKIPIF 1 < 0 ，使 SKIPIF 1 < 0 ， SKIPIF 1 < 0 可证明 SKIPIF 1 < 0 SKIPIF 1 < 0 SKIPIF 1 < 0 ，根据相似三角形比例关系得 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 三点共线时， SKIPIF 1 < 0 取得最小值，再根据等腰直角三角形的性质以及勾股定理进一步计算即可．
【详解】
解：（1） SKIPIF 1 < 0 二次函数 SKIPIF 1 < 0 的图象经过 SKIPIF 1 < 0 ，且与 SKIPIF 1 < 0 轴交于原点及点 SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，二次函数表达式可设为： SKIPIF 1 < 0
将 SKIPIF 1 < 0 ， SKIPIF 1 < 0 代入 SKIPIF 1 < 0 得：
SKIPIF 1 < 0 解这个方程组得 SKIPIF 1 < 0
∵二次函数的函数表达式为 SKIPIF 1 < 0
（2）∵点 SKIPIF 1 < 0 为二次函数图像的顶点，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0
∴顶点坐标为： SKIPIF 1 < 0 ，
设直线 SKIPIF 1 < 0 的函数表达式为 SKIPIF 1 < 0 ，则有：
SKIPIF 1 < 0 解之得： SKIPIF 1 < 0
∴直线 SKIPIF 1 < 0 的函数表达式为 SKIPIF 1 < 0
（3） SKIPIF 1 < 0 是等腰直角三角形，
过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，易知其坐标为 SKIPIF 1 < 0
∵ SKIPIF 1 < 0 的三个顶点分别是 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0
SKIPIF 1 < 0
且满足 SKIPIF 1 < 0
∴ SKIPIF 1 < 0 是等腰直角三角形
（4）如图，以 SKIPIF 1 < 0 为圆心， SKIPIF 1 < 0 为半径作圆，则点 SKIPIF 1 < 0 在圆周上，依题意知：
动点 SKIPIF 1 < 0 的运动时间为 SKIPIF 1 < 0
在 SKIPIF 1 < 0 上取点 SKIPIF 1 < 0 ，使 SKIPIF 1 < 0 ，
连接 SKIPIF 1 < 0 ，则在 SKIPIF 1 < 0 和 SKIPIF 1 < 0 中，
满足： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ∴ SKIPIF 1 < 0 SKIPIF 1 < 0 SKIPIF 1 < 0 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
从而得： SKIPIF 1 < 0
∴ SKIPIF 1 < 0
显然当 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 三点共线时， SKIPIF 1 < 0 取得最小值，
过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，由于 SKIPIF 1 < 0 ，
且 SKIPIF 1 < 0 为等腰直角三角形，
则有 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴动点 SKIPIF 1 < 0 的运动时间 SKIPIF 1 < 0 的最小值为：
SKIPIF 1 < 0 ．
【点睛】
本题主要考查待定系数法求函数解析式，抛物线顶点坐标，等腰直角三角形的性质与判定，相似三角形的判定与性质等知识点，将运动时间的最小值转换为线段长度的最小值是解题的关键．
7.如图，已知抛物线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 轴交于点 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 ，（点 SKIPIF 1 < 0 在点 SKIPIF 1 < 0 的左边），与 SKIPIF 1 < 0 轴交于点 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 为抛物线的顶点，连接 SKIPIF 1 < 0 ．直线 SKIPIF 1 < 0 经过点 SKIPIF 1 < 0 ，且与 SKIPIF 1 < 0 轴交于点 SKIPIF 1 < 0 ．
（1）求抛物线的解析式；
（2）点 SKIPIF 1 < 0 是抛物线上的一点，当 SKIPIF 1 < 0 是以 SKIPIF 1 < 0 为腰的等腰三角形时，求点 SKIPIF 1 < 0 的坐标；
（3）点 SKIPIF 1 < 0 为线段 SKIPIF 1 < 0 上的一点，点 SKIPIF 1 < 0 为线段 SKIPIF 1 < 0 上的一点，连接 SKIPIF 1 < 0 ，并延长 SKIPIF 1 < 0 与线段 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 （点 SKIPIF 1 < 0 在第一象限）．当 SKIPIF 1 < 0 且 SKIPIF 1 < 0 时，求出点 SKIPIF 1 < 0 的坐标．
【答案】（1） SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0 ； SKIPIF 1 < 0 SKIPIF 1 < 0 ；（3） SKIPIF 1 < 0
【分析】
（1）直接利用待定系数法求出a、b的值即可得出抛物线解析式；
（2）当 SKIPIF 1 < 0 时，根据抛物线对称性可求得N的坐标；当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 在 SKIPIF 1 < 0 的垂直平分线上，与抛物线产生两个交点，将两点坐标求出即可；
（3）在 SKIPIF 1 < 0 上取一点 SKIPIF 1 < 0 ，作 SKIPIF 1 < 0 的垂直平分线交 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，在 SKIPIF 1 < 0 上 SKIPIF 1 < 0 点的右侧作 SKIPIF 1 < 0 ，移动 SKIPIF 1 < 0 点，当 SKIPIF 1 < 0 时，点 SKIPIF 1 < 0 为所求，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 垂直于 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 垂直于 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，设 SKIPIF 1 < 0 ，根据相似三角形性质列比例求解，解出点F的坐标即可．
【详解】
（1）将 SKIPIF 1 < 0 代入 SKIPIF 1 < 0 得：
SKIPIF 1 < 0
解得： SKIPIF 1 < 0
∴抛物线的解析式 SKIPIF 1 < 0
（2）顶点 SKIPIF 1 < 0
①当 SKIPIF 1 < 0 时，根据抛物线对称性， SKIPIF 1 < 0 与 SKIPIF 1 < 0 重合
SKIPIF 1 < 0
②方法一：如图一
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 在 SKIPIF 1 < 0 的垂直平分线上
如图 SKIPIF 1 < 0 的垂直平分线交 SKIPIF 1 < 0 于 SKIPIF 1 < 0 ，交 SKIPIF 1 < 0 轴于 SKIPIF 1 < 0 点， SKIPIF 1 < 0 与 SKIPIF 1 < 0 轴交点为 SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0 ，
在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 是 SKIPIF 1 < 0 的中点， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
设 SKIPIF 1 < 0 ，
代入得 SKIPIF 1 < 0 ，
解得： SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
联立得，
SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
方法二：如图二，
过 SKIPIF 1 < 0 作 SKIPIF 1 < 0 轴垂线交 SKIPIF 1 < 0 轴于 SKIPIF 1 < 0 ，
过 SKIPIF 1 < 0 作 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于 SKIPIF 1 < 0 ，
设 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
解得： SKIPIF 1 < 0 ，
把 SKIPIF 1 < 0 代入， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
综上 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
（3）如图一，在 SKIPIF 1 < 0 上取一点 SKIPIF 1 < 0 ，作 SKIPIF 1 < 0 的垂直平分线交 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，在 SKIPIF 1 < 0 上 SKIPIF 1 < 0 点的右侧作 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
移动 SKIPIF 1 < 0 点，当 SKIPIF 1 < 0 时，点 SKIPIF 1 < 0 为所求．
过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 垂直于 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 垂直于 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
设 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴在 SKIPIF 1 < 0 中，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
代入 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 代入 SKIPIF 1 < 0 得，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ．
【点睛】
本题主要考查待定系数法求二次函数解析式，二次函数与几何图形综合，二次函数与一次函数综合，解直角三角形，相似三角形等知识点，题型难度大，属于中考压轴题．
8.已知抛物线y＝ax2+bx+c（a≠0）与x轴交于A、B两点（点A在点B的左边），与y轴交于点C（0，﹣3），顶点D的坐标为（1，﹣4）．
（1）求抛物线的解析式．
（2）在y轴上找一点E，使得△EAC为等腰三角形，请直接写出点E的坐标．
（3）点P是x轴上的动点，点Q是抛物线上的动点，是否存在点P、Q，使得以点P、Q、B、D为顶点，BD为一边的四边形是平行四边形？若存在，请求出点P、Q坐标；若不存在，请说明理由．
【分析】（1）根据抛物线的顶点坐标设出抛物线的解析式，再将点C坐标代入求解，即可得出结论；
（2）先求出点A，C坐标，设出点E坐标，表示出AE，CE，AC，再分三种情况建立方程求解即可；
（3）利用平移先确定出点Q的纵坐标，代入抛物线解析式求出点Q的横坐标，即可得出结论．
【解析】（1）∵抛物线的顶点为（1，﹣4），
∴设抛物线的解析式为y＝a（x﹣1）2﹣4，
将点C（0，﹣3）代入抛物线y＝a（x﹣1）2﹣4中，得a﹣4＝﹣3，
∴a＝1，
∴抛物线的解析式为y＝a（x﹣1）2﹣4＝x2﹣2x﹣3；
（2）由（1）知，抛物线的解析式为y＝x2﹣2x﹣3，
令y＝0，则x2﹣2x﹣3＝0，
∴x＝﹣1或x＝3，
∴B（3，0），A（﹣1，0），
令x＝0，则y＝﹣3，
∴C（0，﹣3），
∴AC，
设点E（0，m），则AE，CE＝|m+3|，
∵△ACE是等腰三角形，
∴①当AC＝AE时，，
∴m＝3或m＝﹣3（点C的纵坐标，舍去），
∴E（0，3），
②当AC＝CE时，|m+3|，
∴m＝﹣3±，
∴E（0，﹣3）或（0，﹣3），
③当AE＝CE时，|m+3|，
∴m，
∴E（0，），
即满足条件的点E的坐标为（0，3）、（0，﹣3）、（0，﹣3）、（0，）；
（3）如图，存在，∵D（1，﹣4），
∴将线段BD向上平移4个单位，再向右（或向左）平移适当的距离，使点B的对应点落在抛物线上，这样便存在点Q，此时点D的对应点就是点P，
∴点Q的纵坐标为4，
设Q（t，4），
将点Q的坐标代入抛物线y＝x2﹣2x﹣3中得，t2﹣2t﹣3＝4，
∴t＝1+2或t＝1﹣2，
∴Q（1+2，4）或（1﹣2，4），
分别过点D，Q作x轴的垂线，垂足分别为F，G，
∵抛物线y＝x2﹣2x﹣3与x轴的右边的交点B的坐标为（3，0），且D（1，﹣4），
∴FB＝PG＝3﹣1＝2，
∴点P的横坐标为（1+2）﹣2＝﹣1+2或（1﹣2）﹣2＝﹣1﹣2，
即P（﹣1+2，0）、Q（1+2，4）或P（﹣1﹣2，0）、Q（1﹣2，4）．
如图，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，AC，BC．M为线段OB上的一个动点，过点M作PM⊥x轴，交抛物线于点P，交BC于点Q．
（1）求抛物线的表达式；
（2）过点P作PN⊥BC，垂足为点N．设M点的坐标为M（m，0），请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？
（3）试探究点M在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标；若不存在，请说明理由．
【分析】（1）将点A、B的坐标代入抛物线表达式，即可求解；
（2）PN＝PQsin45°（m2m）（m﹣2）2，即可求解；
（3）分AC＝CQ、AC＝AQ、CQ＝AQ三种情况，分别求解即可．
【解析】（1）将点A、B的坐标代入抛物线表达式得，解得，
故抛物线的表达式为：yx2x+4；
（2）由抛物线的表达式知，点C（0，4），
由点B、C的坐标得，直线BC的表达式为：y＝﹣x+4；
设点M（m，0），则点P（m，m2m+4），点Q（m，﹣m+4），
∴PQm2m+4+m﹣4m2m，
∵OB＝OC，故∠ABC＝∠OCB＝45°，
∴∠PQN＝∠BQM＝45°，
∴PN＝PQsin45°（m2m）（m﹣2）2，
∵0，故当m＝2时，PN有最大值为；
（3）存在，理由：
点A、C的坐标分别为（﹣3，0）、（0，4），则AC＝5，
①当AC＝CQ时，过点Q作QE⊥y轴于点E，
则CQ2＝CE2+EQ2，即m2+[4﹣（﹣m+4）]2＝25，
解得：m＝±（舍去负值），
故点Q（，）；
②当AC＝AQ时，则AQ＝AC＝5，
在Rt△AMQ中，由勾股定理得：[m﹣（﹣3）]2+（﹣m+4）2＝25，解得：m＝1或0（舍去0），
故点Q（1，3）；
③当CQ＝AQ时，则2m2＝[m＝（﹣3）]2+（﹣m+4）2，解得：m（舍去）；
综上，点Q的坐标为（1，3）或（，）．
10.如图，抛物线与x轴交于点和点，与y轴交于点C，顶点为D，连接与抛物线的对称轴l交于点E．
（1）求抛物线的表达式；
（2）点P是第一象限内抛物线上的动点，连接，当时，求点P的坐标；
（3）点N是对称轴l右侧抛物线上的动点，在射线上是否存在点M，使得以点M，N，E为顶点的三角形与相似？若存在，求点M的坐标；若不存在，请说明理由．
【答案】（1）；（2）；（3）在射线上存在点M，使得以点M，N，E为顶点的三角形与相似，点M的坐标为：，或．
【解析】
【分析】
（1）直接将和点代入，解出a，b的值即可得出答案；
（2）先求出点C的坐标及直线BC的解析式，再根据图及题意得出三角形PBC的面积；过点P作PG轴，交轴于点G，交BC于点F，设，根据三角形PBC的面积列关于t的方程，解出t的值，即可得出点P的坐标；
（3）由题意得出三角形BOC为等腰直角三角形，然后分MN=EM，MN=NE，NE=EM三种情况讨论结合图形得出边之间的关系，即可得出答案．
【详解】
（1）抛物线过点和点
抛物线解析式为：
（2）当时，
直线BC解析式为：
过点P作PG轴，交轴于点G，交BC于点F
设
即
（3）
为等腰直角三角形
抛物线的对称轴为
点E的横坐标为3
又点E在直线BC上
点E的纵坐标为5
设
①当MN=EM，,时
解得或（舍去）
此时点M的坐标为
②当ME=EN，时
解得：或（舍去）
此时点M的坐标为
③当MN=EN，时
连接CM，易知当N为C关于对称轴l的对称点时，，
此时四边形CMNE为正方形
解得：（舍去）
此时点M的坐标为
在射线上存在点M，使得以点M，N，E为顶点的三角形与相似，点M的坐标为：，或．
【点睛】
本题是一道综合题，涉及到二次函数的综合、相似三角形的判定及性质、等腰三角形的性质、勾股定理、正方形的性质等知识点，综合性比较强，解答类似题的关键是添加合适的辅助线．
11.已知直线与抛物线（b，c为常数，）的一个交点为，点是x轴正半轴上的动点．
（1）当直线与抛物线（b，c为常数，）的另一个交点为该抛物线的顶点E时，求k，b，c的值及抛物线顶点E的坐标；
（2）在（1）的条件下，设该抛物线与y轴的交点为C，若点Q在抛物线上，且点Q的横坐标为b，当时，求m的值；
（3）点D在抛物线上，且点D的横坐标为，当的最小值多时，求b的值．
【答案】（1）-2，2，-3，；（2）3或7；（3）3
【解析】
【分析】
（1）由题意可知直线经过，因而把代入直线即可求出k的值，然后把代入抛物线得出含b的代数式表达c，再根据直线与抛物线（b，c为常数，）的另一个交点得出抛物线的顶点坐标E，并代入直线，解方程即可求出b的值，代入即可求解；
（2）由（1）可知直线的解析式是，抛物线的解析式为，根据题意使求出C的坐标，使求出Q的坐标，根据已知条件作图，延长EQ交x轴于点B，因为点D在y轴上且在直线上，所以令时求出点D的坐标，看图可知AO是△ACE以CD为底的高，设E到y轴的距离为，是△CED以CD为底的高，因此可以求出，根据求出，设点E和Q所在直线的解析式为，求出点B的坐标，设点Q和点E到x轴的距离分别为，是△EMB以MB为底的高，是△BQM以MB为底的高，再根据求解，即可求出m的值；
（3）将点D的横坐标代入抛物线（b，c为常数，），根据点A的坐标得到含b的代数式表达c，求出点D的纵坐标为，可知点D在第四象限，且在直线的右侧，取点，过点D作直线AN的垂线，垂足为G，DG与x轴相交于点M，过点D作QH⊥x轴于点H，则点H，在Rt△MDH中，可知，由题意可知点，用含b的代数式表示m，因，可得方程，求解即可得出答案．
【详解】
解：（1）∵直线经过，
∴把代入直线，可得，解得；
∵抛物线（b，c为常数，）经过，
∴把代入抛物线，可得，
∵当直线与抛物线（b，c为常数，）的另一个交点为该抛物线的顶点E，
∴顶点的坐标为，把代入直线，
可得，
∴，解得，
∵，∴，∴，
∴顶点的坐标为．
（2）由（1）可知直线的解析式是，抛物线的解析式为，
∵抛物线与y轴的交点为C，
∴令，C的坐标为，
∵点Q在抛物线上，且点Q的横坐标为b，
由（1）可知，∴，
∴Q的坐标为．
延长EQ交x轴于点B，如图1所示，
∵D在y轴上，且在直线上，
∴当时，点D的坐标为，
∵AO是△ACE以CD为底的高，设E到y轴的距离为，是△CED以CD为底的高，
∴，
∴．
设点E和Q所在直线的解析式为，
把点E和点Q代入，解得：，∴该直线的解析式为，
令，求得点B的坐标为．
设点Q和点E到x轴的距离分别为，是△EMB以MB为底的高，是△BQM以MB为底的高，
∴，
解得：或7，．
（3）∵点D在抛物线（b，c为常数，）上，且点D的横坐标为，
∴，
∵在抛物线（b，c为常数，）上，
∴，即，
∴，
可知点D在第四象限，且在直线的右侧．
∵，
∴可取点，
如图2，过点D作直线AN的垂线，垂足为G，DG与x轴相交于点M，
∴，得，
则此时点M满足题意，过点D作QH⊥x轴于点H，则点H，
在Rt△MDH中，可知，
∴，
∵点，
∴，解得：，
∵，
∴，
∴．
【点睛】
本题是二次函数综合题，主要考查了待定系数法求解析式、二次函数的性质、等腰三角形的性质、三角形的面积公式等知识点，解题的关键是学会使用待定系数法求出抛物线的解析式．
12.如图，抛物线交x轴于两点，交y轴于点C．直线经过点．
（1）求抛物线的解析式；
（2）抛物线的对称轴l与直线相交于点P，连接，判定的形状，并说明理由；
（3）在直线上是否存在点M，使与直线的夹角等于的2倍？若存在，请求出点M的坐标；若不存在，请说明理由．
【答案】（1）；（2）的为直角三角形，理由见解析；（3）存在使与直线的夹角等于的2倍的点，且坐标为M1（），M2（，）．
【解析】
【分析】
（1）先根据直线经过点，即可确定B、C的坐标，然后用带定系数法解答即可；
（2）先求出A、B的坐标结合抛物线的对称性，说明三角形APB为等腰三角形；再结合OB=OC得到∠ABP=45°，进一步说明∠APB=90°，则∠APC=90°即可判定的形状；
（3）作AN⊥BC于N，NH⊥x轴于H，作AC的垂直平分线交BC于M1，AC于E；然后说明△ANB为等腰直角三角形，进而确定N的坐标；再求出AC的解析式，进而确定M1E的解析式；然后联立直线BC和M1E的解析式即可求得M1的坐标；在直线BC上作点M1关于N点的对称点M2，利用中点坐标公式即可确定点M2的坐标
【详解】
解：（1）∵直线经过点
∴当x=0时，可得y=5，即C的坐标为（0,5）
当y=0时，可得x=5，即B的坐标为（5,0）
∴解得
∴该抛物线的解析式为
（2）的为直角三角形，理由如下：
∵解方程=0，则x1=1，x2=5
∴A（1,0），B（5,0）
∵抛物线的对称轴l为x=3
∴△APB为等腰三角形
∵C的坐标为（5,0）, B的坐标为（5,0）
∴OB=CO=5,即∠ABP=45°
∴∠ABP=45°，
∴∠APB=180°-45°-45°=90°
∴∠APC=180°-90°=90°
∴的为直角三角形；
（3）如图：作AN⊥BC于N，NH⊥x轴于H，作AC的垂直平分线交BC于M1，AC于E，
∵M1A=M1C，
∴∠ACM1=∠CAM1
∴∠AM1B=2∠ACB
∵△ANB为等腰直角三角形.
∴AH=BH=NH=2
∴N（3，2）
设AC的函数解析式为y=kx+b
∵C(0，5),A(1，0)
∴ 解得b=5，k=-5
∴AC的函数解析式为y=-5x+5
设EM1的函数解析式为y=x+n
∵点E的坐标为（）
∴=× +n，解得：n=
∴EM1的函数解析式为y=x+
∵ 解得
∴M1的坐标为（）；
在直线BC上作点M1关于N点的对称点M2
设M2（a，-a+5）
则有：3=，解得a=
∴-a+5=
∴M2的坐标为（，）．
综上，存在使与直线的夹角等于的2倍的点，且坐标为M1（），M2（，）．
【点睛】
本题属于二次函数与几何的综合题，主要考查了待定系数法确定函数解析式、等腰直角三角形的判定与性质、一次函数图像、三角形外角等知识，考查知识点较多，综合应用所学知识成为解答本题的关键．
13.如图1所示，在平面直角坐标系中，抛物线与轴交于点和点，与轴交于点．
（1）求抛物线的表达式；
（2）如图2，将抛物线先向左平移1个单位，再向下平移3个单位，得到抛物线，若抛物线与抛物线相交于点，连接，，．
①求点的坐标；
②判断的形状，并说明理由；
（3）在（2）的条件下，抛物线上是否存在点，使得为等腰直角三角形，若存在，求出点的坐标；若不存在，请说明理由．

【答案】（1）；（2）①点的坐标；②是等腰直角三角形，理由见解析；（3）或．
【解析】
【分析】
（1）将点代入即可得；
（2）①先根据二次函数的平移规律得出抛物线的表达式，再联立两条抛物线的表达式求解即可得；
②先根据抛物线的表达式求出点B、C的坐标，再利用两点之间的距离公式分别求出BC、BD、CD的长，然后根据勾股定理的逆定理、等腰三角形的定义即可得；
（3）设点P的坐标为，根据等腰直角三角形的定义分三种情况：①当时，先根据等腰直角三角形的性质、线段中点的点坐标求出点P的坐标，再代入抛物线的表达式，检验点P是否在抛物线的表达式上即可；②当时，先根据平行四边形的判定得出四边形BCDP是平行四边形，再根据点C至点B的平移方式与点D至点P的平移方式相同可求出点P的坐标，然后代入抛物线的表达式，检验点P是否在抛物线的表达式上即可；③当时，先根据等腰直角三角形的性质得出点P在在线段BD的垂直平分线上，再利用待定系数法求出BD的垂直平分线上所在直线的解析式，然后根据两点之间的距离公式和可求出点P的坐标，最后代入抛物线的表达式，检验点P是否在抛物线的表达式上即可．
【详解】
（1）将点代入抛物线的表达式得：
解得
则抛物线的表达式为
故抛物线的表达式为；
（2）①由二次函数的平移规律得：抛物线的表达式为
即
联立，解得
则点的坐标为；
②对于
当时，，解得或
则点B的坐标为
当时，，则点C的坐标为
由两点之间的距离公式得：
则，
故是等腰直角三角形；
（3）抛物线的表达式为
设点P的坐标为
由题意，分以下三种情况：
①当时，为等腰直角三角形
是等腰直角三角形，，
点D是CP的中点
则，解得
即点P的坐标为
对于抛物线的表达式
当时，
即点在抛物线上，符合题意
②当时，为等腰直角三角形
，
，
四边形BCDP是平行四边形
点C至点B的平移方式与点D至点P的平移方式相同
点C至点B的平移方式为先向下平移4个单位长度，再向右平移2个单位长度
即点P的坐标为
对于抛物线的表达式
当时，
即点在抛物线上，符合题意
③当时，为等腰直角三角形
则点P在线段BD的垂直平分线上
设直线BD的解析式
将点代入得：，解得
则直线BD的解析式
设BD的垂线平分线所在直线的解析式为
点的中点的坐标为，即
将点代入得：，解得
则BD的垂线平分线所在直线的解析式为
因此有，即点P的坐标为
由两点之间的距离公式得：
又，为等腰直角三角形
则
解得或
当时，，即点P的坐标为
当时，，即点P的坐标为
对于抛物线的表达式
当时，
即点不在抛物线上，不符合题意，舍去
当时，
即点不在抛物线上，不符合题意，舍去
综上，符合条件的点P的坐标为或．
【点睛】
本题考查了利用待定系数法求二次函数的解析式、二次函数图象的平移，点坐标的平移、等腰直角三角形的判定与性质等知识点，较难的是题（3），正确分三种情况，结合等腰直角三角形的性质是解题关键．
14.如图，抛物线 SKIPIF 1 < 0 交x轴于 SKIPIF 1 < 0 ， SKIPIF 1 < 0 两点，与y轴交于点C，AC，BC．M为线段OB上的一个动点，过点M作 SKIPIF 1 < 0 轴，交抛物线于点P，交BC于点Q．
（1）求抛物线的表达式；
（2）过点P作 SKIPIF 1 < 0 ，垂足为点N．设M点的坐标为 SKIPIF 1 < 0 ，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？
（3）试探究点M在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标；若不存在，请说明理由．
【答案】（1） SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时，PN有最大值，最大值为 SKIPIF 1 < 0 ． （3）满足条件的点Q有两个，坐标分别为： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
【解析】
【分析】
（1）将点A、B的坐标代入解析式中求解即可；
（2）由(1)求得点C坐标，利用待定系数法求得直线BC的解析式，然后用m表示出PN，再利用二次函数的性质即可求解；
（3）分三种情况：①AC=CQ；②AC=AQ；③CQ=AQ，分别求解即可．
【详解】
解：（1）将 SKIPIF 1 < 0 ， SKIPIF 1 < 0 代入 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，解之，得 SKIPIF 1 < 0 ．
所以，抛物线的表达式为 SKIPIF 1 < 0 ．
（2）由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ．
将点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 代入 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，解之，得 SKIPIF 1 < 0 ．
所以，直线BC的表达式为： SKIPIF 1 < 0 ．
由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
∴ SKIPIF 1 < 0
∵ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ．
∴ SKIPIF 1 < 0 ．
∴ SKIPIF 1 < 0 ．
SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0
∴当 SKIPIF 1 < 0 时，PN有最大值，最大值为 SKIPIF 1 < 0 ．
（3）存在，理由如下：由点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，知 SKIPIF 1 < 0 ．
①当 SKIPIF 1 < 0 时，过Q作 SKIPIF 1 < 0 轴于点E，易得 SKIPIF 1 < 0 ，
由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 （舍）
此时，点 SKIPIF 1 < 0 ；
②当 SKIPIF 1 < 0 时，则 SKIPIF 1 < 0 ．
在 SKIPIF 1 < 0 中，由勾股定理，得 SKIPIF 1 < 0 ．
解之，得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 （舍）
此时，点 SKIPIF 1 < 0 ；
③当 SKIPIF 1 < 0 时，
由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 （舍）．
综上知所述，可知满足条件的点Q有两个，坐标分别为： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
【点睛】
本题是一道二次函数与几何图形的综合题，解答的关键是认真审题，找出相关条件，运用待定系数法、数形结合法等解题方法确定解题思路，对相关信息进行推理、探究、发现和计算．