2024年中考数学二轮题型突破练习题型11 综合探究题 类型1 非动态探究题（专题训练）（2份打包，原卷版+教师版）

这是一份2024年中考数学二轮题型突破练习题型11 综合探究题 类型1 非动态探究题（专题训练）（2份打包，原卷版+教师版），文件包含2024年中考数学二轮题型突破练习题型11综合探究题类型1非动态探究题专题训练原卷版doc、2024年中考数学二轮题型突破练习题型11综合探究题类型1非动态探究题专题训练教师版doc等2份试卷配套教学资源，其中试卷共68页， 欢迎下载使用。

(1)若正方形 SKIPIF 1 < 0 的边长为2，E是 SKIPIF 1 < 0 的中点．
①如图1，当 SKIPIF 1 < 0 时，求证： SKIPIF 1 < 0 ；
②如图2，当 SKIPIF 1 < 0 时，求 SKIPIF 1 < 0 的长；
(2)如图3，延长 SKIPIF 1 < 0 ， SKIPIF 1 < 0 交于点G，当 SKIPIF 1 < 0 时，求证： SKIPIF 1 < 0 ．
【答案】(1)①详见解析；② SKIPIF 1 < 0
(2)详见解析
【分析】（1）①由 SKIPIF 1 < 0 ，证明 SKIPIF 1 < 0 ，可得结论；②如图，延长 SKIPIF 1 < 0 ， SKIPIF 1 < 0 交于点G作 SKIPIF 1 < 0 ，垂足为H，证明 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，设 SKIPIF 1 < 0 可得 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，证明 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，从而可得答案；
（2）如图，延长 SKIPIF 1 < 0 ，作 SKIPIF 1 < 0 ，垂足为H，证明 SKIPIF 1 < 0 ，设 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，由 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，由 SKIPIF 1 < 0 可得 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，证明 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，从而可得答案．
【详解】（1）解：如图，

正方形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，
① SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
②如图，

延长 SKIPIF 1 < 0 ， SKIPIF 1 < 0 交于点G，
作 SKIPIF 1 < 0 ，垂足为H，
SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
方法一：设 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
SKIPIF 1 < 0 在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
方法二：在 SKIPIF 1 < 0 中，由 SKIPIF 1 < 0 ，设 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ；
（2）如图

延长 SKIPIF 1 < 0 ，作 SKIPIF 1 < 0 ，垂足为H，
SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
设 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ．
【点睛】本题考查的是正方形的性质，勾股定理的应用，相似三角形的判定与性质，锐角三角函数的应用，本题计算量大，对学生的要求高，熟练的利用参数建立方程是解本题的关键．
2.(2021·四川省达州市)某数学兴趣小组在数学课外活动中，对多边形内两条互相垂直的线段做了如下探究：
【观察与猜想】
如图，在正方形中，点，分别是，上的两点，连接，，，则的值为______ ；
如图，在矩形中，，，点是上的一点，连接，，且，则的值为______ ；
【类比探究】
如图，在四边形中，，点为上一点，连接，过点作的垂线交的延长线于点，交的延长线于点，求证：；
【拓展延伸】
如图，在中，，，，将沿翻折，点落在点处得，点，分别在边，上，连接，，．
求的值；
连接，若，直接写出的长度．
解：如图，设与交于点，
四边形是正方形，
，，
，
，
，，
，
在和中，
，
≌，
，
；
如图，设与交于点，
四边形是矩形，
，
，
，
，，
，
，
∽，
，
故答案为：．
证明：如图，过点作交的延长线于点，
，
，
四边形为矩形，
，，
，，
∽，
，
，
；
如图，过点作于点，连接交于点，与相交于点，
，，
，
，，
∽，
，
在中，，，
，
在中，，
，
设，则，
，
，
负值舍去，
，，
，
，
，
，
；
，，，
，
由得：∽，
，
又，，
，
，
．
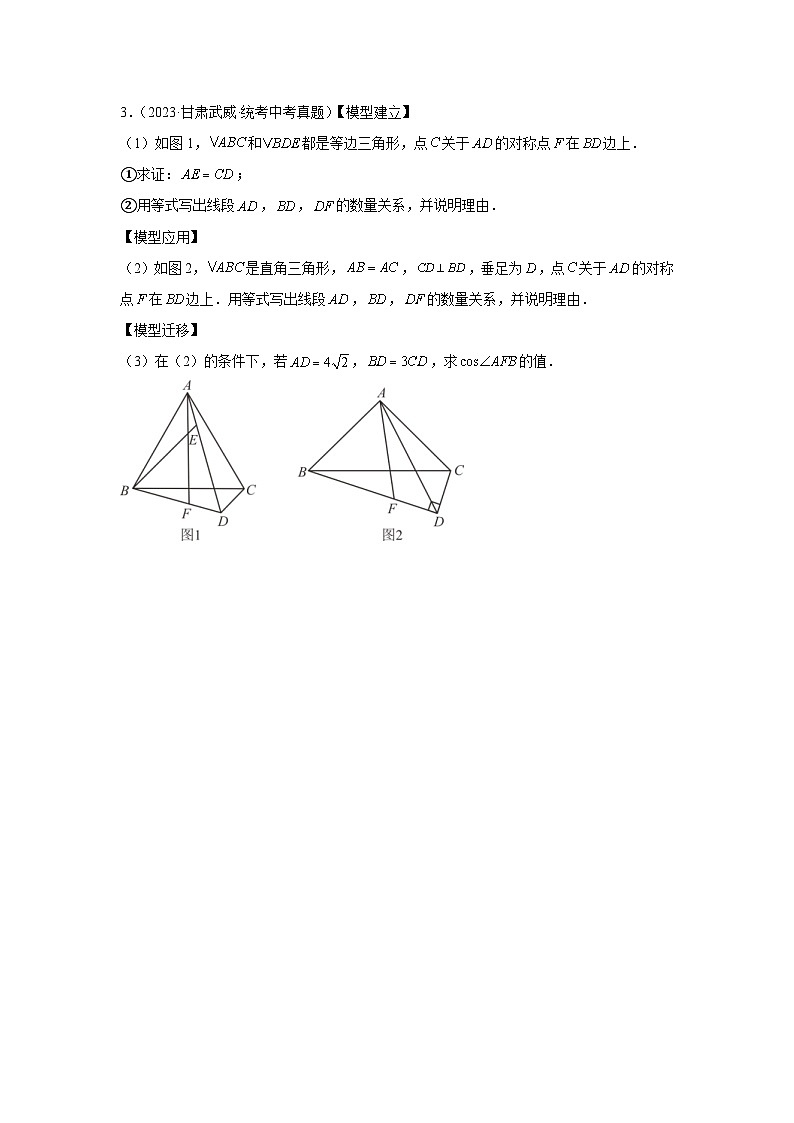
3．（2023·甘肃武威·统考中考真题）【模型建立】
（1）如图1， SKIPIF 1 < 0 和 SKIPIF 1 < 0 都是等边三角形，点 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 的对称点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 边上．
①求证： SKIPIF 1 < 0 ；
②用等式写出线段 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的数量关系，并说明理由．
【模型应用】
（2）如图2， SKIPIF 1 < 0 是直角三角形， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，垂足为 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 的对称点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 边上．用等式写出线段 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的数量关系，并说明理由．
【模型迁移】
（3）在（2）的条件下，若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的值．

【答案】（1）①见解析；② SKIPIF 1 < 0 ，理由见解析；（2） SKIPIF 1 < 0 ，理由见解析；（3） SKIPIF 1 < 0
【分析】（1）①证明： SKIPIF 1 < 0 ，再证明 SKIPIF 1 < 0 即可；②由 SKIPIF 1 < 0 和 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称，可得 SKIPIF 1 < 0 ．证明 SKIPIF 1 < 0 ，从而可得结论；
（2）如图，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，证明 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．可得 SKIPIF 1 < 0 ，证明 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，从而可得结论；
（3）由 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，结合 SKIPIF 1 < 0 ，求解 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，如图，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ．可得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，再利用余弦的定义可得答案．
【详解】（1）①证明：∵ SKIPIF 1 < 0 和 SKIPIF 1 < 0 都是等边三角形，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
∴ SKIPIF 1 < 0 ．

② SKIPIF 1 < 0 ．理由如下：
∵ SKIPIF 1 < 0 和 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称，
∴ SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
∴ SKIPIF 1 < 0 ．
（2） SKIPIF 1 < 0 ．理由如下：
如图，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ．

∵ SKIPIF 1 < 0 和 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
∴ SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 是直角三角形， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
∴ SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ．
（3）∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
如图，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ．

∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ．
∴ SKIPIF 1 < 0 ．
∴ SKIPIF 1 < 0 ．
【点睛】本题考查的是全等三角形的判定与性质，等边三角形的性质，勾股定理的应用，轴对称的性质，锐角三角函数的灵活应用，本题难度较高，属于中考压轴题，作出合适的辅助线是解本题的关键．
4.（2021·湖北中考真题）问题提出 如图（1），在 SKIPIF 1 < 0 和 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 内部，直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 ，线段 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 之间存在怎样的数量关系？
问题探究 （1）先将问题特殊化．如图（2），当点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 重合时，直接写出一个等式，表示 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 之间的数量关系；
（2）再探究一般情形．如图（1），当点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 不重合时，证明（1）中的结论仍然成立．
问题拓展 如图（3），在 SKIPIF 1 < 0 和 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 （ SKIPIF 1 < 0 是常数），点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 内部，直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 ，直接写出一个等式，表示线段 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 之间的数量关系．
【答案】（1） SKIPIF 1 < 0 ．（2）见解析；问题拓展： SKIPIF 1 < 0 ．
【分析】
（1）先证明△BCE≌△ACD,得到AF=BE，BF-BE=BF-AF=EF= SKIPIF 1 < 0 ；
（2）过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，证明 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 是等腰直角三角形即可；利用前面的方法变全等为相似证明即可．
【详解】
问题探究 （1） SKIPIF 1 < 0 ．理由如下：如图（2），
∵∠BCA=∠ECF=90°，
∴∠BCE=∠ACF，
∵BC=AC，EC=CF，
△BCE≌△ACF，
∴BE=AF，
∴BF-BE=BF-AF=EF= SKIPIF 1 < 0 ；
（2）证明：过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
又∵ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
∴ SKIPIF 1 < 0 ．
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 是等腰直角三角形．
∴ SKIPIF 1 < 0 ．
∴ SKIPIF 1 < 0 ．
问题拓展 SKIPIF 1 < 0 ．理由如下：
∵∠BCA=∠ECD=90°，
∴∠BCE=∠ACD，
∵BC=kAC，EC=kCD，
∴△BCE∽△ACD，
∴∠EBC=∠FAC，
过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点M，则 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
∴△BCM∽△ACF，
∴BM:AF=BC:AC=MC:CF=k，
∴BM=kAF,MC=kCF，
∴BF-BM=MF，MF= SKIPIF 1 < 0 = SKIPIF 1 < 0
∴BF- kAF = SKIPIF 1 < 0 ．
【点睛】
本题考查了等腰直角三角形的性质，三角形全等的判定和性质，三角形相似的判定和性质，勾股定理，熟练掌握三角形全等的判定，三角形相似的判定，勾股定理是解题的关键．
5．（2023·湖北武汉·统考中考真题）问题提出：如图（1）， SKIPIF 1 < 0 是菱形 SKIPIF 1 < 0 边 SKIPIF 1 < 0 上一点， SKIPIF 1 < 0 是等腰三角形， SKIPIF 1 < 0 ， SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，探究 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的数量关系．

问题探究：
(1)先将问题特殊化，如图（2），当 SKIPIF 1 < 0 时，直接写出 SKIPIF 1 < 0 的大小；
(2)再探究一般情形，如图（1），求 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的数量关系．
问题拓展：
(3)将图（1）特殊化，如图（3），当 SKIPIF 1 < 0 时，若 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的值．
【答案】(1) SKIPIF 1 < 0
(2) SKIPIF 1 < 0
(3) SKIPIF 1 < 0
【分析】（1）延长 SKIPIF 1 < 0 过点F作 SKIPIF 1 < 0 ，证明 SKIPIF 1 < 0 即可得出结论．
（2）在 SKIPIF 1 < 0 上截取 SKIPIF 1 < 0 ，使 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，证明 SKIPIF 1 < 0 ，通过边和角的关系即可证明．
（3）过点A作 SKIPIF 1 < 0 的垂线交 SKIPIF 1 < 0 的延长线于点 SKIPIF 1 < 0 ，设菱形的边长为 SKIPIF 1 < 0 ，由（2）知， SKIPIF 1 < 0 ，通过相似求出 SKIPIF 1 < 0 ，即可解出．
【详解】（1）延长 SKIPIF 1 < 0 过点F作 SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
在 SKIPIF 1 < 0 和 SKIPIF 1 < 0 中
SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．

故答案为： SKIPIF 1 < 0 ．
（2）解：在 SKIPIF 1 < 0 上截取 SKIPIF 1 < 0 ，使 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ．
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ．
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ．
SKIPIF 1 < 0 ．
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ．
SKIPIF 1 < 0
SKIPIF 1 < 0 ．

（3）解：过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 的垂线交 SKIPIF 1 < 0 的延长线于点 SKIPIF 1 < 0 ，设菱形的边长为 SKIPIF 1 < 0 ，
SKIPIF 1 < 0
SKIPIF 1 < 0 ．
在 SKIPIF 1 < 0 中，
SKIPIF 1 < 0
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ．
SKIPIF 1 < 0 ，由（2）知， SKIPIF 1 < 0 ．
SKIPIF 1 < 0
SKIPIF 1 < 0 ．
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
在 SKIPIF 1 < 0 上截取 SKIPIF 1 < 0 ，使 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，作 SKIPIF 1 < 0 于点O．
由（2）知， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
SKIPIF 1 < 0
SKIPIF 1 < 0 ．

【点睛】此题考查菱形性质、三角形全等、三角形相似，解题的关键是熟悉菱形性质、三角形全等、三角形相似．
6.（2021·浙江中考真题）（证明体验）
（1）如图1， SKIPIF 1 < 0 为 SKIPIF 1 < 0 的角平分线， SKIPIF 1 < 0 ，点E在 SKIPIF 1 < 0 上， SKIPIF 1 < 0 ．求证： SKIPIF 1 < 0 平分 SKIPIF 1 < 0 ．
（思考探究）
（2）如图2，在（1）的条件下，F为 SKIPIF 1 < 0 上一点，连结 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点G．若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的长．
（拓展延伸）
（3）如图3，在四边形 SKIPIF 1 < 0 中，对角线 SKIPIF 1 < 0 平分 SKIPIF 1 < 0 ，点E在 SKIPIF 1 < 0 上， SKIPIF 1 < 0 ．若 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的长．
【答案】（1）见解析；（2） SKIPIF 1 < 0 ；（3） SKIPIF 1 < 0
【分析】
（1）根据SAS证明 SKIPIF 1 < 0 ，进而即可得到结论；
（2）先证明 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，进而即可求解；
（3）在 SKIPIF 1 < 0 上取一点F，使得 SKIPIF 1 < 0 ，连结 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，从而得 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，最后证明 SKIPIF 1 < 0 ，即可求解．
【详解】
解：（1）∵ SKIPIF 1 < 0 平分 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 平分 SKIPIF 1 < 0 ；
（2）∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ；
（3）如图，在 SKIPIF 1 < 0 上取一点F，使得 SKIPIF 1 < 0 ，连结 SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 平分 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 ，
又∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
【点睛】
本题主要考查全等三角形的判定和性质，相似三角形的判定和性质，添加辅助线，构造全等三角形和相似三角形，是解题的关键．
7．（2023·山东·统考中考真题）（1）如图1，在矩形 SKIPIF 1 < 0 中，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别在边 SKIPIF 1 < 0 ， SKIPIF 1 < 0 上， SKIPIF 1 < 0 ，垂足为点 SKIPIF 1 < 0 ．求证： SKIPIF 1 < 0 ．

【问题解决】
（2）如图2，在正方形 SKIPIF 1 < 0 中，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别在边 SKIPIF 1 < 0 ， SKIPIF 1 < 0 上， SKIPIF 1 < 0 ，延长 SKIPIF 1 < 0 到点 SKIPIF 1 < 0 ，使 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ．求证： SKIPIF 1 < 0 ．
【类比迁移】
（3）如图3，在菱形 SKIPIF 1 < 0 中，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别在边 SKIPIF 1 < 0 ， SKIPIF 1 < 0 上， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的长．
【答案】（1）见解析
（2）见解析
（3）3
【分析】（1）由矩形的性质可得 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，再由 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，根据等角的余角相等得 SKIPIF 1 < 0 ，即可得证；
（2）利用“ SKIPIF 1 < 0 ”证明 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，由 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，利用“ SKIPIF 1 < 0 ”证明 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，由正方形的性质可得 SKIPIF 1 < 0 ，根据平行线的性质，即可得证；
（3）延长 SKIPIF 1 < 0 到点 SKIPIF 1 < 0 ，使 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，由菱形的性质可得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，推出 SKIPIF 1 < 0 ，由全等的性质可得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，进而推出 SKIPIF 1 < 0 是等边三角形，再根据线段的和差关系计算求解即可．
【详解】（1）证明： SKIPIF 1 < 0 四边形 SKIPIF 1 < 0 是矩形，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ；
（2）证明： SKIPIF 1 < 0 四边形 SKIPIF 1 < 0 是正方形，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 的延长线上，
SKIPIF 1 < 0 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ；
（3）解：如图，延长 SKIPIF 1 < 0 到点 SKIPIF 1 < 0 ，使 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，

SKIPIF 1 < 0 四边形 SKIPIF 1 < 0 是菱形，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 是等边三角形，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ．
【点睛】本题是四边形综合题，主要考查了矩形的性质，正方形的性质，菱形的性质，相似三角形的判定，全等三角形的判定和性质，等边三角形的判定和性质，熟练掌握这些知识点并灵活运用是解题的关键．
8.（2021·安徽中考真题）如图1，在四边形ABCD中， SKIPIF 1 < 0 ，点E在边BC上，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，作 SKIPIF 1 < 0 交线段AE于点F，连接BF．
（1）求证： SKIPIF 1 < 0 ；
（2）如图2，若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求BE的长；
（3）如图3，若BF的延长线经过AD的中点M，求 SKIPIF 1 < 0 的值．
【答案】（1）见解析；（2）6；（3） SKIPIF 1 < 0
【分析】
（1）根据平行线的性质及已知条件易证 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，即可得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；再证四边形AFCD是平行四边形即可得 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，根据SAS即可证得 SKIPIF 1 < 0 ；
（2）证明 SKIPIF 1 < 0 ，利用相似三角形的性质即可求解；
（3）延长BM、ED交于点G．易证 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ；设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，由此可得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；再证明 SKIPIF 1 < 0 ，根据全等三角形的性质可得 SKIPIF 1 < 0 ．证明 SKIPIF 1 < 0 ，根据相似三角形的性质可得 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，解方程求得x的值，继而求得 SKIPIF 1 < 0 的值．
【详解】
（1）证明： SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ；
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 四边形AFCD是平行四边形
SKIPIF 1 < 0
SKIPIF 1 < 0
在 SKIPIF 1 < 0 与 SKIPIF 1 < 0 中．
SKIPIF 1 < 0 ，
SKIPIF 1 < 0
（2） SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
在 SKIPIF 1 < 0 与 SKIPIF 1 < 0 中．
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ；
SKIPIF 1 < 0 ；
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ；
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ；
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 或 SKIPIF 1 < 0 （舍）；
（3）延长BM、ED交于点G．
SKIPIF 1 < 0 与 SKIPIF 1 < 0 均为等腰三角形， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ；
在 SKIPIF 1 < 0 与 SKIPIF 1 < 0 中，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ；
SKIPIF 1 < 0 ．
SKIPIF 1 < 0 ；
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 （舍）， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ．
【点睛】
本题是三角形综合题，考查了全等三角形的性质及判定、相似三角形的性质及判定，熟练判定三角形全等及相似是解决问题的关键．
9．（2023·黑龙江·统考中考真题）如图①， SKIPIF 1 < 0 和 SKIPIF 1 < 0 是等边三角形，连接 SKIPIF 1 < 0 ，点F，G，H分别是 SKIPIF 1 < 0 和 SKIPIF 1 < 0 的中点，连接 SKIPIF 1 < 0 ．易证： SKIPIF 1 < 0 ．
若 SKIPIF 1 < 0 和 SKIPIF 1 < 0 都是等腰直角三角形，且 SKIPIF 1 < 0 ，如图②：若 SKIPIF 1 < 0 和 SKIPIF 1 < 0 都是等腰三角形，且 SKIPIF 1 < 0 ，如图③：其他条件不变，判断 SKIPIF 1 < 0 和 SKIPIF 1 < 0 之间的数量关系，写出你的猜想，并利用图②或图③进行证明．

【答案】图②中 SKIPIF 1 < 0 ，图③中 SKIPIF 1 < 0 ，证明见解析
【分析】图②：如图②所示，连接 SKIPIF 1 < 0 ，先由三角形中位线定理得到 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，再证明 SKIPIF 1 < 0 得到 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，进一步证明 SKIPIF 1 < 0 ，即可证明 SKIPIF 1 < 0 是等腰直角三角形，则 SKIPIF 1 < 0 ；
图③：仿照图②证明 SKIPIF 1 < 0 是等边三角形，则 SKIPIF 1 < 0 ．
【详解】解：图②中 SKIPIF 1 < 0 ，图③中 SKIPIF 1 < 0 ，
图②证明如下：
如图②所示，连接 SKIPIF 1 < 0 ，
∵点F，G分别是 SKIPIF 1 < 0 的中点，
∴ SKIPIF 1 < 0 是 SKIPIF 1 < 0 的中位线，
∴ SKIPIF 1 < 0 ，
同理可得 SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 和 SKIPIF 1 < 0 都是等腰直角三角形，且 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 是等腰直角三角形，
∴ SKIPIF 1 < 0 ；

图③证明如下：
如图③所示，连接 SKIPIF 1 < 0 ，
∵点F，G分别是 SKIPIF 1 < 0 的中点，
∴ SKIPIF 1 < 0 是 SKIPIF 1 < 0 的中位线，
∴ SKIPIF 1 < 0 ，
同理可得 SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 和 SKIPIF 1 < 0 都是等腰三角形，且 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 是等边三角形，
∴ SKIPIF 1 < 0 ．

【点睛】本题主要考查了全等三角形的性质与判定，三角形中位线定理，等边三角形的性质与判定，勾股定理等等，正确作出辅助线构造全等三角形是解题的关键．
10.（2021·湖南中考真题）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，N是 SKIPIF 1 < 0 边上的一点，D为 SKIPIF 1 < 0 的中点，过点A作 SKIPIF 1 < 0 的平行线交 SKIPIF 1 < 0 的延长线于T，且 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ．
（1）求证： SKIPIF 1 < 0 ；
（2）在如图中 SKIPIF 1 < 0 上取一点O，使 SKIPIF 1 < 0 ，作N关于边 SKIPIF 1 < 0 的对称点M，连接 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 得如图．
①求证： SKIPIF 1 < 0 ；
②设 SKIPIF 1 < 0 与 SKIPIF 1 < 0 相交于点P，求证： SKIPIF 1 < 0 ．
【答案】(1)见解析；(2)①见解析，②见解析．
【分析】
（1）先用 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 证明出四边形ATBN是平行四边形，得到△TAD≌△CND，用对应边相等与等量代换，从而得出结论．
（2）①连接AM、MN，利用矩形的性质与等腰三角形的性质，证明出△OCM是直角三角形，证明出Rt△OAT≌Rt△OCM，得到对应角相等，则得到答案；
②连接OP，由①中 SKIPIF 1 < 0 ，得到∠OTM=∠OAP，点O、T、A、P共圆，由直径所对的圆周角为直角，证明出∠OPT=90︒，再根据等腰三角形的三线合一性得出结论．
【详解】
证明：（1）∵ SKIPIF 1 < 0 ，且 SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，
∴四边形ATBN是平行四边形，
∴ SKIPIF 1 < 0 ，
∴∠DTA=∠DCN，
∵∠ADT=∠NDC，
∵点D为AN的中点，
∴AD=ND，
∴△TAD≌△CND（AAS）
∴TA=CN，
∵ SKIPIF 1 < 0 ，
∴BN=CN，
（2）①如图所示，连接AM、MN，
∵点N关于边 SKIPIF 1 < 0 的对称点为M，
∴△ANC≌△AMC，
∴∠ACN=∠ACM，
∵AB=AC，点N为AC的中点，
∴平行四边形ATBN是矩形，
∴∠TAB=∠ABN=∠ACN=∠ACM，∠BAN=∠MAC=∠CAN，AT=BN=NC=MC，
∵OA=OC，
∴∠CAN=∠ACO，
∴∠TAB+∠BAN=∠ACM+∠ACO=90︒，
∴∠OAT=∠OCM=90︒，
在Rt△OAT和Rt△OCM中，
∵AT=CM，∠OAT=∠OCM ，OA=OC，
∴Rt△OAT≌Rt△OCM（SAS），
∴∠AOT=∠COM，OT=OM，
∴∠AOT+∠AOM=∠COM+∠AOM，
∴∠TOM=∠AOC
∵OA=OC，OT=OM，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ；
②如图所示，连接OP，
∵ SKIPIF 1 < 0 ，
∴∠OTM=∠OAP，
∴点O、T、A、P共圆，
∵∠OAT=90︒，
∴OT为圆的直径，
∴∠OPT=90︒，
∵OT=OM，
∴点P为TM的中点，
∵由（1）得△TAD≌△CND，
∴TD=CD，
∴点D为TC的中点，
∴DP为△TCM的中位线，
∴ SKIPIF 1 < 0 ．
【点睛】
本题主要考查了矩形的判定与性质、等腰三角形的性质、三角形全等的判定与性质、以及相似三角形的判定与性质、圆中直径的性质，关键在于通过等量代换，换出角相等，证明出直角三角形全等，再证明三角形相似．
11．（2023·广东深圳·统考中考真题）（1）如图，在矩形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 为 SKIPIF 1 < 0 边上一点，连接 SKIPIF 1 < 0 ，
①若 SKIPIF 1 < 0 ，过 SKIPIF 1 < 0 作 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，求证： SKIPIF 1 < 0 ；
②若 SKIPIF 1 < 0 时，则 SKIPIF 1 < 0 ______．

（2）如图，在菱形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，过 SKIPIF 1 < 0 作 SKIPIF 1 < 0 交 SKIPIF 1 < 0 的延长线于点 SKIPIF 1 < 0 ，过 SKIPIF 1 < 0 作 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 时，求 SKIPIF 1 < 0 的值．

（3）如图，在平行四边形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上，且 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 为 SKIPIF 1 < 0 上一点，连接 SKIPIF 1 < 0 ，过 SKIPIF 1 < 0 作 SKIPIF 1 < 0 交平行四边形 SKIPIF 1 < 0 的边于点 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 时，请直接写出 SKIPIF 1 < 0 的长．

【答案】（1）①见解析；② SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0 ；（3） SKIPIF 1 < 0 或 SKIPIF 1 < 0 或 SKIPIF 1 < 0
【分析】（1）①根据矩形的性质得出 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，进而证明 SKIPIF 1 < 0 结合已知条件，即可证明 SKIPIF 1 < 0 ；
②由①可得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，证明 SKIPIF 1 < 0 ，得出 SKIPIF 1 < 0 ，根据 SKIPIF 1 < 0 ，即可求解；
（2）根据菱形的性质得出 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，根据已知条件得出 SKIPIF 1 < 0 ，证明 SKIPIF 1 < 0 ，根据相似三角形的性质即可求解；
（3）分三种情况讨论，①当点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 边上时，如图所示，延长 SKIPIF 1 < 0 交 SKIPIF 1 < 0 的延长线于点 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，证明 SKIPIF 1 < 0 ，解 SKIPIF 1 < 0 ，进而得出 SKIPIF 1 < 0 ，根据 SKIPIF 1 < 0 ，得出 SKIPIF 1 < 0 ，建立方程解方程即可求解；②当 SKIPIF 1 < 0 点在 SKIPIF 1 < 0 边上时，如图所示，连接 SKIPIF 1 < 0 ，延长 SKIPIF 1 < 0 交 SKIPIF 1 < 0 的延长线于点 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，四边形 SKIPIF 1 < 0 是平行四边形，同理证明 SKIPIF 1 < 0 ，根据 SKIPIF 1 < 0 得出 SKIPIF 1 < 0 ，建立方程，解方程即可求解；③当 SKIPIF 1 < 0 点在 SKIPIF 1 < 0 边上时，如图所示，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，求得 SKIPIF 1 < 0 ，而 SKIPIF 1 < 0 ，得出矛盾，则此情况不存在．
【详解】解：（1）①∵四边形 SKIPIF 1 < 0 是矩形，则 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
又∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
又∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ；
②由①可得 SKIPIF 1 < 0 ， SKIPIF 1 < 0
∴ SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，
又∵ SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ,
故答案为： SKIPIF 1 < 0 ．
（2）∵在菱形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ， SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ,
又 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 SKIPIF 1 < 0 ；
（3）①当点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 边上时，如图所示，延长 SKIPIF 1 < 0 交 SKIPIF 1 < 0 的延长线于点 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，

∵平行四边形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ,
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
∴ SKIPIF 1 < 0 SKIPIF 1 < 0
在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
∴ SKIPIF 1 < 0
∴ SKIPIF 1 < 0
∴ SKIPIF 1 < 0
设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
解得： SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
②当 SKIPIF 1 < 0 点在 SKIPIF 1 < 0 边上时，如图所示，

连接 SKIPIF 1 < 0 ，延长 SKIPIF 1 < 0 交 SKIPIF 1 < 0 的延长线于点 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，四边形 SKIPIF 1 < 0 是平行四边形，
设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0
∴ SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0
∴ SKIPIF 1 < 0
过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，
在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0
SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
即 SKIPIF 1 < 0
解得： SKIPIF 1 < 0 （舍去）
即 SKIPIF 1 < 0 ；
③当 SKIPIF 1 < 0 点在 SKIPIF 1 < 0 边上时，如图所示，

过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，
在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 点不可能在 SKIPIF 1 < 0 边上，
综上所述， SKIPIF 1 < 0 的长为 SKIPIF 1 < 0 或 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ．
【点睛】本题考查了相似三角形的性质与判定，平行四边形的性质，解直角三角形，矩形的性质，熟练掌握相似三角形的性质与判定，分类讨论是解题的关键．
12.（2020•山西）综合与实践
问题情境：
如图①，点E为正方形ABCD内一点，∠AEB＝90°，将Rt△ABE绕点B按顺时针方向旋转90°，得到△CBE′（点A的对应点为点C）．延长AE交CE′于点F，连接DE．
猜想证明：
（1）试判断四边形BE'FE的形状，并说明理由；
（2）如图②，若DA＝DE，请猜想线段CF与FE'的数量关系并加以证明；
解决问题：
（3）如图①，若AB＝15，CF＝3，请直接写出DE的长．
【分析】（1）由旋转的性质可得∠AEB＝∠CE'B＝90°，BE＝BE'，∠EBE'＝90°，由正方形的判定可证四边形BE'FE是正方形；
（2）过点D作DH⊥AE于H，由等腰三角形的性质可得AHAE，DH⊥AE，由“AAS”可得△ADH≌△BAE，可得AH＝BEAE，由旋转的性质可得AE＝CE'，可得结论；
（3）利用勾股定理可求BE＝BE'＝9，再利用勾股定理可求DE的长．
【解析】（1）四边形BE'FE是正方形，
理由如下：
∵将Rt△ABE绕点B按顺时针方向旋转90°，
∴∠AEB＝∠CE'B＝90°，BE＝BE'，∠EBE'＝90°，
又∵∠BEF＝90°，
∴四边形BE'FE是矩形，
又∵BE＝BE'，
∴四边形BE'FE是正方形；
（2）CF＝E'F；
理由如下：如图②，过点D作DH⊥AE于H，
∵DA＝DE，DH⊥AE，
∴AHAE，DH⊥AE，
∴∠ADH+∠DAH＝90°，
∵四边形ABCD是正方形，
∴AD＝AB，∠DAB＝90°，
∴∠DAH+∠EAB＝90°，
∴∠ADH＝∠EAB，
又∵AD＝AB，∠AHD＝∠AEB＝90°，
∴△ADH≌△BAE（AAS），
∴AH＝BEAE，
∵将Rt△ABE绕点B按顺时针方向旋转90°，
∴AE＝CE'，
∵四边形BE'FE是正方形，
∴BE＝E'F，
∴E'FCE'，
∴CF＝E'F；
（3）如图①，过点D作DH⊥AE于H，
∵四边形BE'FE是正方形，
∴BE'＝E'F＝BE，
∵AB＝BC＝15，CF＝3，BC2＝E'B2+E'C2，
∴225＝E'B2+（E'B+3）2，
∴E'B＝9＝BE，
∴CE'＝CF+E'F＝12，
由（2）可知：BE＝AH＝9，DH＝AE＝CE'＝12，
∴HE＝3，
∴DE3．
13.（2020•湘西州）问题背景：如图1，在四边形ABCD中，∠BAD＝90°，∠BCD＝90°，BA＝BC，∠ABC＝120°，∠MBN＝60°，∠MBN绕B点旋转，它的两边分别交AD、DC于E、F．探究图中线段AE，CF，EF之间的数量关系．
小李同学探究此问题的方法是：延长FC到G，使CG＝AE，连接BG，先证明△BCG≌△BAE，再证明△BFG≌△BFE，可得出结论，他的结论就是 ；
探究延伸1：如图2，在四边形ABCD中，∠BAD＝90°，∠BCD＝90°，BA＝BC，∠ABC＝2∠MBN，∠MBN绕B点旋转．它的两边分别交AD、DC于E、F，上述结论是否仍然成立？请直接写出结论（直接写出“成立”或者“不成立”），不要说明理由；
探究延伸2：如图3，在四边形ABCD中，BA＝BC，∠BAD+∠BCD＝180°，∠ABC＝2∠MBN，∠MBN绕B点旋转．它的两边分别交AD、DC于E、F．上述结论是否仍然成立？并说明理由；
实际应用：如图4，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处．舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以75海里/小时的速度前进，同时舰艇乙沿北偏东50°的方向以100海里/小时的速度前进，1.2小时后，指挥中心观测到甲、乙两舰艇分别到达E、F处．且指挥中心观测两舰艇视线之间的夹角为70°．试求此时两舰艇之间的距离．
【分析】问题背景：延长FC到G，使CG＝AE，连接BG，先证明△BCG≌△BAE，再证明△BFG≌△BFE，即可得出结论：EF＝AE+CF；
探究延伸1：延长FC到G，使CG＝AE，连接BG，先证明△BCG≌△BAE，再证明△BFG≌△BFE，可得出结论：EF＝AE+CF；
探究延伸2：延长DC到H，使得CH＝AE，连接BH，先证明△BCH≌△BAE，即可得到BE＝HB，∠ABE＝∠HBC，再证明△HBF≌△EBF，即可得出EF＝HF＝HC+CF＝AE+CF；
实际应用：连接EF，延长BF交AE的延长线于G，根据题意可转化为如下的数学问题：在四边形GAOB中，OA＝OB，∠A+∠B＝180°，∠AOB＝2∠EOF，∠EOF的两边分别交AG，BG于E，F，求EF的长．再根据探究延伸2的结论：EF＝AE+BF，即可得到两舰艇之间的距离．
【解析】问题背景：
如图1，延长FC到G，使CG＝AE，连接BG，先证明△BCG≌△BAE，再证明△BFG≌△BFE，可得出结论：EF＝AE+CF；
故答案为：EF＝AE+CF；
探究延伸1：
如图2，延长FC到G，使CG＝AE，连接BG，先证明△BCG≌△BAE，再证明△BFG≌△BFE，可得出结论：EF＝AE+CF；
探究延伸2：
上述结论仍然成立，即EF＝AE+CF，理由：
如图3，延长DC到H，使得CH＝AE，连接BH，
∵∠BAD+∠BCD＝180°，∠BCH+∠BCD＝180°，
∴∠BCH＝∠BAE，
∵BA＝BC，CH＝AE，
∴△BCH≌△BAE（SAS），
∴BE＝HB，∠ABE＝∠HBC，
∴∠HBE＝∠ABC，
又∵∠ABC＝2∠MBN，
∴∠EBF＝∠HBF，
∵BF＝BF，
∴△HBF≌△EBF（SAS），
∴EF＝HF＝HC+CF＝AE+CF；
实际应用：
如图4，连接EF，延长BF交AE的延长线于G，
因为舰艇甲在指挥中心（O处）北偏西30°的A处．舰艇乙在指挥中心南偏东70°的B处，所以∠AOB＝140°，
因为指挥中心观测两舰艇视线之间的夹角为70°，所以∠EOF＝70°，所以∠AOB＝2∠EOF．
依题意得，OA＝OB，∠A＝60°，∠B＝120°，所以∠A+∠B＝180°，
因此本题的实际的应用可转化为如下的数学问题：
在四边形GAOB中，OA＝OB，∠A+∠B＝180°，∠AOB＝2∠EOF，∠EOF的两边分别交AG，B于E，F，求EF的长．
根据探究延伸2的结论可得：EF＝AE+BF，
根据题意得，AE＝75×1.2＝90（海里），BF＝100×1.2＝120（海里），
所以EF＝90+120＝210（海里）．
答：此时两舰艇之间的距离为210海里．
14.（2020•扬州）如图1，已知点O在四边形ABCD的边AB上，且OA＝OB＝OC＝OD＝2，OC平分∠BOD，与BD交于点G，AC分别与BD、OD交于点E、F．
（1）求证：OC∥AD；
（2）如图2，若DE＝DF，求的值；
（3）当四边形ABCD的周长取最大值时，求的值．
【分析】（1）由等腰三角形的性质及角平分线的定义证得∠ADO＝∠DOC，则可得出结论；
（2）过点E作EM∥FD交AD的延长线于点M，证得∠M＝∠ADF＝45°，由直角三角形的性质得出EMDEDF，证明△AME∽△ADF，得出；
（3）设BC＝CD＝x，CG＝m，则OG＝2﹣m，由勾股定理得出4﹣（2﹣m）2＝x2﹣m2，解得：m，可用x表示四边形ABCD的周长，根据二次函数的性质可求出x＝2时，四边形ABCD有最大值，得出∠ADF＝∠DOC＝60°，∠DAE＝30°，由直角三角形的性质可得出答案．
【解答】（1）证明：∵AO＝OD，
∴∠OAD＝∠ADO，
∵OC平分∠BOD，
∴∠DOC＝∠COB，
又∵∠DOC+∠COB∠＝∠OAD+∠ADO，
∴∠ADO＝∠DOC，
∴CO∥AD；
（2）解：如图1，过点E作EM∥FD交AD的延长线于点M，
设∠DAC＝α，
∵CO∥AD，
∴∠ACO＝∠DAC＝α，
∵AO＝OC，
∴∠OAC＝∠OCA＝α，
∵OA＝OD，
∴∠ODA＝∠OAD＝2α，
∵DE＝EF，
∴∠DFE＝∠DEF＝3α，
∵AO＝OB＝OD，
∴∠ADB＝90°，
∴∠DAE+∠AED＝90°，
即4α＝90°，
∴∠ADF＝2α＝45°，
∴∠FDE＝45°，
∴∠M＝∠ADF＝45°，
∴EMDEDF，
∵DF∥EM，
∴△AME∽△ADF，
∴；
（3）解：如图2，
∵OD＝OB，∠BOC＝∠DOC，
∴△BOC≌△DOC（SAS），
∴BC＝CD，
设BC＝CD＝x，CG＝m，则OG＝2﹣m，
∵OB2﹣OG2＝BC2﹣CG2，
∴4﹣（2﹣m）2＝x2﹣m2，
解得：m，
∴OG＝2，
∵OD＝OB，∠DOG＝∠BOG，
∴G为BD的中点，
又∵O为AB的中点，
∴AD＝2OG＝4，
∴四边形ABCD的周长为2BC+AD+AB＝2x+442x+810，
∵0，
∴x＝2时，四边形ABCD的周长有最大值为10．
∴BC＝2，
∴△BCO为等边三角形，
∴∠BOC＝60°，
∵OC∥AD，
∴∠DAC＝∠COB＝60°，
∴∠ADF＝∠DOC＝60°，∠DAE＝30°，
∴∠AFD＝90°，
∴，DFDA，
∴．
15.（2020•南京）如图①，要在一条笔直的路边l上建一个燃气站，向l同侧的A、B两个城镇分别铺设管道输送燃气．试确定燃气站的位置，使铺设管道的路线最短．
（1）如图②，作出点A关于l的对称点A'，线段A'B与直线l的交点C的位置即为所求，即在点C处建燃气站，所得路线ACB是最短的．
为了证明点C的位置即为所求，不妨在直线1上另外任取一点C'，连接AC'、BC'，证明AC+CB＜AC′+C'B．请完成这个证明．
（2）如果在A、B两个城镇之间规划一个生态保护区，燃气管道不能穿过该区域．请分别给出下列两种情形的铺设管道的方案（不需说明理由）．
①生态保护区是正方形区域，位置如图③所示；
②生态保护区是圆形区域，位置如图④所示．
【分析】（1）由轴对称的性质可得CA＝CA'，可得AC+BC＝A'C+BC＝A'B，AC'+C'B＝A'C'+BC'，由三角形的三边关系可得A'B＜A'C'+C'B，可得结论；
（2）①由（1）的结论可求；
②由（1）的结论可求解．
【解答】证明：（1）如图②，连接A'C'，
∵点A，点A'关于l对称，点C在l上，
∴CA＝CA'，
∴AC+BC＝A'C+BC＝A'B，
同理可得AC'+C'B＝A'C'+BC'，
∵A'B＜A'C'+C'B，
∴AC+BC＜AC'+C'B；
（2）如图③，
在点C出建燃气站，铺设管道的最短路线是ACDB，（其中点D是正方形的顶点）；
如图④，
在点C出建燃气站，铺设管道的最短路线是ACDEB，（其中CD，BE都与圆相切）
16.（2020•达州）（1）[阅读与证明]
如图1，在正△ABC的外角∠CAH内引射线AM，作点C关于AM的对称点E（点E在∠CAH内），连接BE，BE、CE分别交AM于点F、G．
①完成证明：∵点E是点C关于AM的对称点，
∴∠AGE＝90°，AE＝AC，∠1＝∠2．
∵正△ABC中，∠BAC＝60°，AB＝AC，
∴AE＝AB，得∠3＝∠4．
在△ABE中，∠1+∠2+60°+∠3+∠4＝180°，∴∠1+∠3＝ °．
在△AEG中，∠FEG+∠3+∠1＝90°，∴∠FEG＝ °．
②求证：BF＝AF+2FG．
（2）[类比与探究]
把（1）中的“正△ABC”改为“正方形ABDC”，其余条件不变，如图2．类比探究，可得：
①∠FEG＝ °；
②线段BF、AF、FG之间存在数量关系 ．
（3）[归纳与拓展]
如图3，点A在射线BH上，AB＝AC，∠BAC＝α（0°＜α＜180°），在∠CAH内引射线AM，作点C关于AM的对称点E（点E在∠CAH内），连接BE，BE、CE分别交AM于点F、G．则线段BF、AF、GF之间的数量关系为 ．
【分析】（1）①利用等腰三角形的性质，三角形内角和定理解决问题即可．
②如图1中，连接CF，在FB上取一点T，使得FT＝CF，连接CT．证明△BCT≌△ACF（SAS可得结论．
（2）①如图2中，利用圆周角定理解决问题即可．
②结论：BFAFFG．如图2中，连接CF，在FB上取一点T，使得FT＝CF，连接CT．证明△BCT∽△ACF，推出，推出BTAF可得结论．
（3）如图3中，连接CF，BC，在BF上取一点T，使得FT＝CF．构造相似三角形，利用相似三角形的性质解决问题即可．
【解答】（1）①解：如图1中，∵点E是点C关于AM的对称点，
∴∠AGE＝90°，AE＝AC，∠1＝∠2．
∵正△ABC中，∠BAC＝60°，AB＝AC，
∴AE＝AB，得∠3＝∠4．
在△ABE中，∠1+∠2+60°+∠3+∠4＝180°，
∴∠1+∠3＝60°．
在△AEG中，∠FEG+∠3+∠1＝90°，
∴∠FEG＝30°．
故答案为60，30．
②证明：如图1中，连接CF，在FB上取一点T，使得FT＝CF，连接CT．
∵C，E关于AM对称，
∴AM垂直平分线段EC，
∴FE＝FC，
∴∠FEC＝∠FCE＝30°，EF＝2FG，
∴∠CFT＝∠FEC+∠FCE＝60°，
∵FC＝FT，
∴△CFT是等边三角形，
∴∠ACB＝∠FCT＝60°，CF＝CT＝FT，
∴∠BCT＝∠ACF，
∵CB＝CA，
∴△BCT≌△ACF（SAS），
∴BT＝AF，
∴BF＝BT+FT＝AF+EF＝AF+2FG．
（2）解：①如图2中，∵AB＝AC＝AE，
∴点A是△ECB的外接圆的圆心，
∴∠BEC∠BAC，
∵∠BAC＝90°，
∴∠FEG＝45°．
故答案为45．
②结论：BFAFFG．
理由：如图2中，连接CF，在FB上取一点T，使得FT＝CF，连接CT．
∵AM⊥EC，CG＝CE，
∴FC＝EF，
∴∠FEC＝∠FCE＝45°，EFFG，
∴∠CFT＝∠FEC+∠FCE＝90°，
∵CF＝CT，
∴△CFT是等腰直角三角形，
∴CTCF，
∵△ABC是等腰直角三角形，
∴BCAC，
∴，
∵∠BCA＝∠TCF＝45°，
∴∠BCT＝∠ACF，
∴△BCT∽△ACF，
∴，
∴BTAF，
∴BF＝BT+TFAFFG．．
（3）如图3中，连接CF，BC，在BF上取一点T，使得FT＝CF．
∵AB＝AC，∠BAC＝α，
∴sinα，
∴2•sinα，
∵AB＝AC＝AE，
∴∠BEC∠BACα，EF，
∵FC＝FE，
∴∠FEC＝∠FCEα，
∴∠CFT＝∠FEC+∠FCE＝α，
同法可证，△BCT∽△ACF，
∴2•sinα，
∴BT＝2AF•sinα，
∴BF＝BT+FT＝2AF•sinα+EF．即BF＝2AF•sinα．
故答案为：BF＝2AF•sinα．