2024年中考数学二轮题型突破练习题型12 二次函数与圆的问题（专题训练）（2份打包，原卷版+教师版）

这是一份2024年中考数学二轮题型突破练习题型12 二次函数与圆的问题（专题训练）（2份打包，原卷版+教师版），文件包含2024年中考数学二轮题型突破练习类型12二次函数与圆的问题专题训练原卷版doc、2024年中考数学二轮题型突破练习类型12二次函数与圆的问题专题训练教师版doc等2份试卷配套教学资源，其中试卷共87页， 欢迎下载使用。

(1)求的长和关于的函数表达式．
(2)当，且长度分别等于，，的三条线段组成的三角形与相似时，求的值．
(3)延长交半圆于点，当时，求的长．
【答案】(1)，
(2)或或
(3)
【分析】（1）如图1，连接，根据切线的性质得出，证明，得出，即可得出；证明四边形是平行四边形，得出，代入数据可得；
（2）根据三边之比为，可分为三种情况．当时，当时，当时，分别列出比例式，进而即可求解．
（3）连接，，过点作于点，根据，得出，由，可得，代入（1）中解析式，即可求解．
【详解】（1）解：如图1，连接．

∵切半圆于点，
∴．
∵，，
∴，
∴．
∵，
∴，
∴，
即，
∴．
如图2，，
∴．

∵，
∴四边形是平行四边形，
∴．
∵，
∴，
∴．
（2）∵，，三边之比为（如图2），
∴可分为三种情况．
i）当时，
，，
解得，
∴．
ii）当时，
，，
解得，
∴．
iii）当时，
，，
解得，
∴．
（3）如图3，连接，，过点作于点，

则，，
∴．
∵，，
∴．
∵，
∴，
∴，
∴，
∴，，
∴，即的长为．
【点睛】本题考查了切线的性质，解直角三角形，相似三角形的性质与判定，函数解析式，分类讨论，作出辅助线是解题的关键．
2．（2023·山东烟台·统考中考真题）如图，抛物线与轴交于两点，与轴交于点．抛物线的对称轴与经过点的直线交于点，与轴交于点．

(1)求直线及抛物线的表达式；
(2)在抛物线上是否存在点，使得是以为直角边的直角三角形?若存在，求出所有点的坐标；若不存在，请说明理由；
(3)以点为圆心，画半径为2的圆，点为上一个动点，请求出的最小值．
【答案】(1)直线的解析式为；抛物线解析式为；(2)存在，点M的坐标为或 或；(3)
【分析】（1）根据对称轴，，得到点A及B的坐标，再利用待定系数法求解析式即可；
（2）先求出点D的坐标，再分两种情况：①当时，求出直线的解析式为，解方程组，即可得到点M的坐标；②当时，求出直线的解析式为，解方程组，即可得到点M的坐标；
（3）在上取点，使，连接，证得，又，得到，推出，进而得到当点C、P、F三点共线时，的值最小，即为线段的长，利用勾股定理求出即可．
【详解】（1）解：∵抛物线的对称轴，，
∴，
将代入直线，得，
解得，
∴直线的解析式为；
将代入，得
，解得，
∴抛物线的解析式为；
（2）存在点，
∵直线的解析式为，抛物线对称轴与轴交于点．
∴当时，，
∴，
①当时，
设直线的解析式为，将点A坐标代入，
得，
解得，
∴直线的解析式为，
解方程组，
得或，
∴点M的坐标为；
②当时，
设直线的解析式为，将代入，
得，
解得，
∴直线的解析式为，
解方程组，
解得或，
∴点M的坐标为 或
综上，点M的坐标为或 或；
（3）如图，在上取点，使，连接，
∵，
∴，
∵，、
∴，
又∵，
∴，
∴，即，
∴，
∴当点C、P、F三点共线时，的值最小，即为线段的长，
∵，
∴，
∴的最小值为．

【点睛】此题是一次函数，二次函数及圆的综合题，掌握待定系数法求函数解析式，直角三角形的性质，勾股定理，相似三角形的判定和性质，求两图象的交点坐标，正确掌握各知识点是解题的关键．
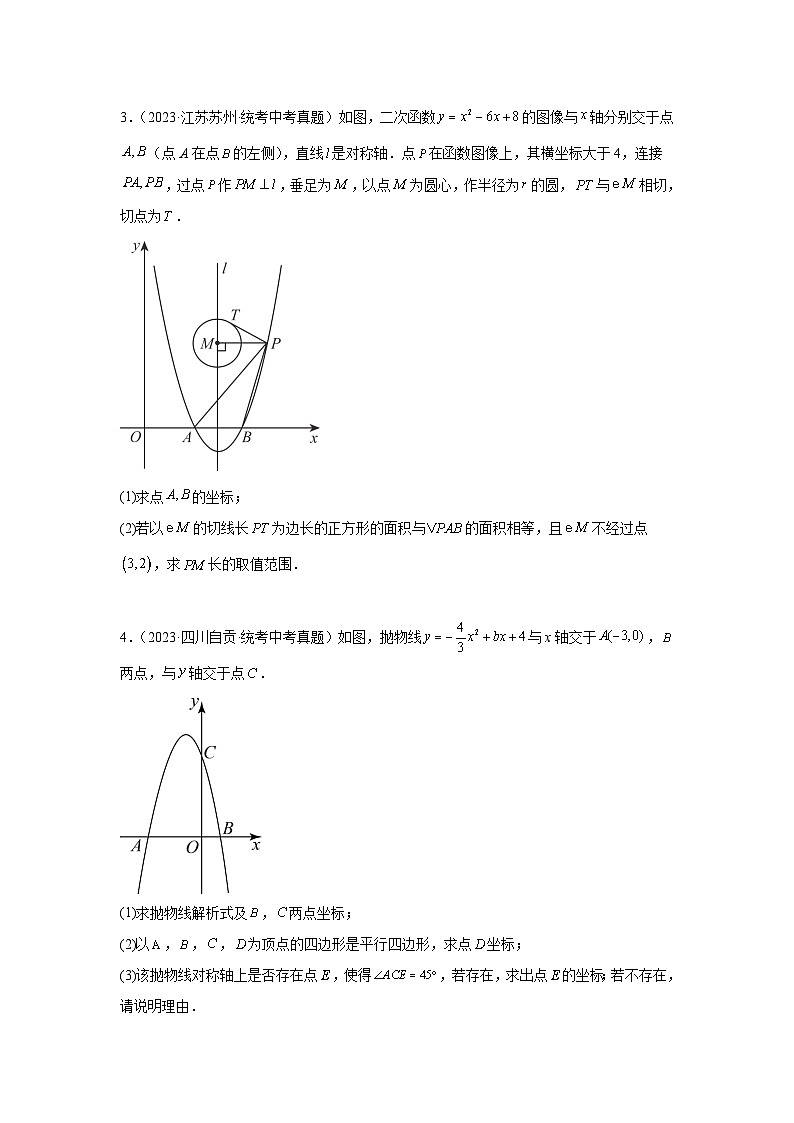
3．（2023·江苏苏州·统考中考真题）如图，二次函数的图像与轴分别交于点（点A在点的左侧），直线是对称轴．点在函数图像上，其横坐标大于4，连接，过点作，垂足为，以点为圆心，作半径为的圆，与相切，切点为．

(1)求点的坐标；
(2)若以的切线长为边长的正方形的面积与的面积相等，且不经过点，求长的取值范围．
【答案】(1)；(2)或或
【分析】（1）令求得点的横坐标即可解答；
（2）由题意可得抛物线的对称轴为，设，则；如图连接，则，进而可得切线长为边长的正方形的面积为；过点P作轴，垂足为H，可得；由题意可得，解得；然后再分当点M在点N的上方和下方两种情况解答即可．
【详解】（1）解：令，则有：，解得：或，
∴．
（2）解：∵抛物线过
∴抛物线的对称轴为，
设，
∵，
∴,
如图：连接，则，
∴，
∴切线为边长的正方形的面积为，
过点P作轴，垂足为H，则：，
∴
∵，
∴，

假设过点,则有以下两种情况：
①如图1：当点M在点N的上方，即

∴，解得：或，
∵
∴；
②如图2：当点M在点N的上方，即

∴，解得：，
∵
∴；
综上，或．
∴当不经过点时，或或．
【点睛】本题主要考查了二次函数的性质、切线的性质、勾股定理等知识点，掌握分类讨论思想是解答本题的关键．
4．（2023·四川自贡·统考中考真题）如图，抛物线与x轴交于，两点，与轴交于点．

(1)求抛物线解析式及，两点坐标；
(2)以，，，为顶点的四边形是平行四边形，求点坐标；
(3)该抛物线对称轴上是否存在点，使得，若存在，求出点的坐标；若不存在，请说明理由．
【答案】(1)抛物线解析式为，，；(2)或或；(3)
【分析】（1）将点代入抛物线解析式，待定系数法求解析式，进而分别令，即可求得两点的坐标；
（2）分三种情况讨论，当，为对角线时，根据中点坐标即可求解；
（3）根据题意，作出图形，作交于点，为的中点，连接，则在上，根据等弧所对的圆周角相等，得出在上，进而勾股定理，根据建立方程，求得点的坐标，进而得出的解析式，即可求解．
【详解】（1）解：∵抛物线与x轴交于，
∴
解得：，
∴抛物线解析式为，
当时，，
∴，
当时，
解得：，
∴
（2）∵，，，
设，
∵以，，，为顶点的四边形是平行四边形
当为对角线时，
解得：，
∴；
当为对角线时，
解得：
∴
当为对角线时，
解得：
∴
综上所述，以，，，为顶点的四边形是平行四边形，或或
（3）解：如图所示，作交于点，为的中点，连接，

∵
∴是等腰直角三角形，
∴在上，
∵，，
∴，，
∵，
∴在上，
设，则
解得：（舍去）
∴点
设直线的解析式为
∴
解得：.
∴直线的解析式
∵，，
∴抛物线对称轴为直线，
当时，，
∴．
【点睛】本题考查了二次函数的综合运用，待定系数法求解析式，平行四边形的性质，圆周角角定理，勾股定理，求一次函数解析式，熟练掌握以上知识是解题的关键．
5．（2023·四川乐山·统考中考真题）已知是抛物（b为常数）上的两点，当时，总有
(1)求b的值；
(2)将抛物线平移后得到抛物线．
探究下列问题：
①若抛物线与抛物线有一个交点，求m的取值范围；
②设抛物线与x轴交于A，B两点，与y轴交于点C，抛物线的顶点为点E，外接圆的圆心为点F，如果对抛物线上的任意一点P，在抛物线上总存在一点Q，使得点P、Q的纵坐标相等．求长的取值范围．
【答案】(1)0；(2)①②
【分析】（1）根据，且时，总有，变形后即可得到结论；
（2）按照临界情形，画出图象分情况讨论求解即可．
【详解】（1）解：由题可知：
时，总有，
．
则，
∴，
∴总成立，且，
；
（2）①注意到抛物线最大值和开口大小不变，m只影响图象左右平移下面考虑满足题意的两种临界情形：
（i）当抛物线过点时，如图所示，

此时，，解得或（舍）．
（ii）当抛物线过点时，如图所示，

此时，，
解得或（舍），
综上，，
②同①考虑满足题意的两种临界情形：
（i）当抛物线过点时，如图所示，

此时，，解得或（舍）．
（ii）当抛物线过点时，如图所示，

此时，，解得或0（舍）．
综上，
如图，由圆的性质可知，点E、F在线段的垂直平分线上．

令，解得，
，
，
，
设，
，
，
，
，
，即，
．
，即，
，
【点睛】此题考查了二次函数的图象和性质、垂径定理、解一元二次方程等知识，数形结合和分类讨论是解题的关键．
6．（2023·四川宜宾·统考中考真题）如图，抛物线与x轴交于点、，且经过点．

(1)求抛物线的表达式；
(2)在x轴上方的抛物线上任取一点N，射线、分别与抛物线的对称轴交于点P、Q，点Q关于x轴的对称点为，求的面积；
(3)点M是y轴上一动点，当最大时，求M的坐标．
【答案】(1)；(2)；(3)
【分析】（1）设抛物线的解析式为，代入点C的坐标，确定a值即可．
（2）设，直线的解析式为，直线的解析式为，表示出P，Q，的坐标，进而计算即可．
（3）当M是y轴与经过A，C，M三点的圆的切点是最大计算即可.
【详解】（1）∵抛物线与x轴交于点、，
∴设抛物线的解析式为，
∵经过点，
∴，
解得，
∴，
∴．
（2）如图，当点N在对称轴的右侧时，
∵，
∴对称轴为直线，

设，直线的解析式为，直线的解析式为，
∴
解得，
∴直线的解析式为，直线的解析式为，
当时，，
，
∴，，，
∴，
∴．
如图，当点N在对称轴的左侧时，
∵，
∴对称轴为直线，

设，，，，
∴，
∴．
综上所述，．
（3）当的外接圆与相切，切点为M时， 最大，
设外接圆的圆心为E，Q是异于点M的一点，连接，，交圆于点T，
则，根据三角形外角性质，得，故，
∴最大，
设与圆交于点H，连接，，根据切线性质，
∴，
作直径，连接，
∴，，
∵，
∴，
∴，
∴，
∴，
∴，
∴，
设，则，
∴，
∴，
过点E作，垂足为F，过点C作，垂足为G，交于点P，
根据垂径定理，得，四边形是矩形，
∴，

根据，得，
∴，
∴，
在直角三角形中，
∴，
∴，
∴，
∴，
解得，（舍去），
∴，
故，
∴当最大时，．
【点睛】此题是二次函数综合题，主要考查了待定系数法，等腰三角形的性质，垂径定理，勾股定理，矩形的判定和性质，三角形的外接圆，相似三角形的判定和性质，用方程的思想解决问题是解本题的关键．
7．（2023·湖北恩施·统考中考真题）在平面直角坐标系中，为坐标原点，已知抛物线与轴交于点，抛物线的对称轴与轴交于点．

(1)如图，若，抛物线的对称轴为．求抛物线的解析式，并直接写出时的取值范围；
(2)在（1）的条件下，若为轴上的点，为轴上方抛物线上的点，当为等边三角形时，求点，的坐标；
(3)若抛物线经过点，，，且，求正整数m，n的值．
【答案】(1)；
(2)；或,；
(3)，或，
【分析】（1）根据，抛物线的对称轴为，待定系数法求解析式即可求解；当时，求得的范围，进而结合函数图象即可求解；
（2）①连接，，交对称轴于点D，由四点共圆，得，证明，求出点D的坐标，确定直线的解析式，进而求得点的坐标，设，，勾股定理即可求解；②由①可得，则当与重合时也存在等边三角形，根据等边三角形的性质即可求解．
（3）根据抛物线经过点，，，可得抛物线对称为直线，则，则，进而令，求得的范围，进而根据函数图象可知或，进而分别讨论求得的值，即可求解．
【详解】（1）解：∵，抛物线的对称轴为．
∴
解得：
∴抛物线解析式为，
当时，即
解得：，
∴当时，
（2）解：①如图所示，连接，，交对称轴于点D，

∵，
∴，
则
∴，，
∵为等边三角形，
∴，
∴，
∴四点共圆，
∴，
∵，
∴．
∴，
∴，
∵，，
∴，
∴，则，
设直线的解析式为
则
解得：
所以直线的解析式为
联立
解得：或
∴，
∵，设，
∵
∴
解得：
∴；
②由①可得，当与点重合时，为等边三角形
则与对称，此时，，
综上所述；；或，；
（3）解：∵抛物线经过点，，，
∴抛物线对称为直线，
则，则
∴抛物线解析式为
∴顶点坐标为
当时，
解得：或
∵，且为正整数，过点，则当时，
∴或，
当时，将点代入解析式，
解得：
∵
则，
当时，将点代入解析式
解得：
∵
则，
综上所述，，或，．
【点睛】本题考查了二次函数的性质，根据特三角函数求角度，圆内接四边形对角互补，二次函数的性质，熟练掌握二次函数的性质是解题的关键．
8.如图1，在平面直角坐标系中，抛物线与x轴分别相交于A、B两点，与y轴相交于点C，下表给出了这条抛物线上部分点的坐标值：
（1）求出这条抛物线的解析式及顶点M的坐标；
（2）是抛物线对称轴上长为1的一条动线段（点P在点Q上方），求的最小值；
（3）如图2，点D是第四象限内抛物线上一动点，过点D作轴，垂足为F，的外接圆与相交于点E．试问：线段的长是否为定值？如果是，请求出这个定值；如果不是，请说明理由．
【答案】（1）；；（2）；（3）是，1．
【分析】
（1）依据表格数据，设出抛物线的顶点式，利用待定系数法求解即可；
（2）利用平移和找对称点的方式，将的长转化为，再利用两点之间线段最短确定的最小值等于CE的长，加1后即能确定的最小值；
（3）设出圆心和D点的坐标，接着表示出E点的坐标，利用圆心到B点的距离等于圆心到D点的距离，求出q和e的关系，得到E点的纵坐标，进而确定EF的长为定值．
【详解】
解：（1）由表格数据可知，顶点坐标为（1,4）
设抛物线解析式为：，
将点（0,3）代入解析式得：3=a+4，
∴，
∴抛物线解析式为：，顶点坐标．
（2）由表格可知，抛物线经过点A（-1,0），C（0,3），
如图3，将A点向上平移一个单位，得到，
则
∴四边形是平行四边形，
∴，
作关于MQ的对称点E，则
∴，
∴，
当P、E、C三点共线时，最短，
设直线CE的解析式为：，
将C、E两点坐标代入解析式可得：，
∴，
∴直线CE的解析式为：，
令，则，
∴当时，P、E、C三点共线，此时最短，
∴的最小值为．
（3）是；
理由：设，
因为A、B两点关于直线x=1对称，
所以圆心位于该直线上，
所以可设的外接圆的圆心为，
作，垂足为点N，则，
由轴，
∴，
∵，且由表格数据可知
∴，
化简得：，
∵点D是第四象限内抛物线上一动点，且抛物线解析式为，
∴，
∴，
∴，
∵，
∴，
∴，
∴，
即的长不变，为1．
【点睛】
本题涉及到了动点问题，综合考查了用待定系数法求抛物线解析式、点的平移、勾股定理、平行四边形的判定与性质、最短路径问题、圆的性质等内容，解决本题的关键是理解并掌握相关概念与公式，能将题干信息与图形相结合，挖掘图中隐含信息，本题有一定的计算量，对学生的综合分析与计算能力都有较高的要求，本题蕴含了数形结合的思想方法等．
9.如图，抛物线（其中）与x轴交于A、B两点，交y轴于点C．
（1）直接写出的度数和线段AB的长（用a表示）；
（2）若点D为的外心，且与的周长之比为，求此抛物线的解析式；
（3）在（2）的前提下，试探究抛物线上是否存在一点P，使得？若存在，求出点P的坐标；若不存在，请说明理由．
【答案】（1）∠OCA=45°，AB= a+1；（2）；（3）存在，P1（，），P2（1，-2）．
【分析】
（1）根据二次函数解析式可得A（a，0），C（0，-a），B（-1，0），即可得出OA=OB=a，OB=1，即可证明△OCA是等腰直角三角形，可得∠OCA=45°，根据线段的和差关系可表示AB的长；
（2）如图，作△ABC的外接圆⊙D，根据等腰直角三角形的性质可得AC=，利用两点间距离公式可用a表示出BC的长，根据圆周角定理可得∠D=2∠OAC=90°，可得△DBC是等腰直角三角形，即可证明△DBC∽△OCA，根据相似三角形周长之比等于相似比列方程求出a值即可得答案；
（3）如图，过点D作DH⊥AB于H，过点C作AC的垂线，交x轴于F，过点O作OG⊥AC于G，连接AP交CF于E，可得△OCF是等腰直角三角形，利用待定系数法可得直线CF的解析式，根据外心的定义及等腰直角三角形的性质可求出点D坐标，即可得出BH、DH的长，根据，∠BHD=∠ACE=90°可证明△BHD∽△ACE，根据相似三角形的性质可求出CE的长，根据两点间距离公式可得点E坐标，利用待定系数法可得直线AE解析式，联立直线AE与抛物线的解析式求出点P坐标即可得答案．
【详解】
（1）∵抛物线（其中）与x轴交于A、B两点，交y轴于点C．
∴当x=0时，y=-a，
当y=0时，，
解得：，，
∴A（a，0），C（0，-a），B（-1，0），
∴OB=1，OA=OC=a，
∴△OCA是等腰直角三角形，
∴∠OCA=45°，AB=OA+OB=a+1．
（2）如图，作△ABC的外接圆⊙D，
∵点D为的外心，
∴DB=DC，
∵△OCA是等腰直角三角形，OA=a，
∴∠OAC=45°，AC=，
∵∠BDC和∠BAC是所对的圆心角和圆周角，
∴∠BDC=2∠BAC=90°，
∴∠DBC=45°，
∴∠DBC=∠OAC，
∴△DBC∽△OCA，
∵与的周长之比为，
∴，即，
解得：，
经检验：是原方程的根，
∵,
∴a=2，
∴抛物线解析式为：=．
（3）如图，过点D作DH⊥AB于H，过点C作AC的垂线，交x轴于F，过点O作OG⊥AC于G，连接AP交CF于E，
∵a=2，
∴C（0，-2），A（2，0），AC=，
∵∠OCA=45°，
∴∠OCF=45°，
∴△OCF是等腰直角三角形，
∴F（-2，0），
设直线CF的解析式为y=kx+b，
∴，
解得：，
∴直线CF的解析式为，
∵△OCA是等腰直角三角形，OG⊥AC，
∴OG所在直线为AC的垂直平分线，点G为AC中点，
∵点D为的外心，
∴点D在直线OG上，
∵A（2，0），C（0，-2），
∴G（1，-1），
设直线OG的解析式y=mx，
∴m=-1，
∴直线OG的解析式y=-x，
∵点D为△ABC的外心，
∴点D在AB的垂直平分线上，
∴点D的横坐标为=，
把x=代入y=-x得y=-，
∴D（，-），
∴DH=，BH=1+=，
∵，∠BHD=∠ACE=90°，
∴△BHD∽△ACE，
∴，即，
解得：，
∵点E在直线CF上，
∴设点E坐标为（n，-n-2），
∴CE==，
解得：，
∴（，），（，），
设直线AE1的解析式为y=k1x+b1，
∴，
解得：，
∴直线AE1的解析式为，
同理：直线AE2的解析式为，
联立直线AE1解析式与抛物线解析式得，
解得：，（与点A重合，舍去），
∴P1（，），
联立直线AE2解析式与抛物线解析式得，
解得：，（与点A重合，舍去），
∴P2（1，-2）．
综上所述：存在点P，使得，点P坐标为P1（，），P2（1，-2）．
【点睛】
本题考查二次函数的综合，考查了二次函数的性质、待定系数法求一次函数解析式、圆周角定理、等腰三角形的性质、相似三角形的判定与性质，熟练掌握相关性质及定理是解题关键
10.如图，已知二次函数的图象经过点且与轴交于原点及点．
（1）求二次函数的表达式；
（2）求顶点的坐标及直线的表达式；
（3）判断的形状，试说明理由；
（4）若点为上的动点，且的半径为，一动点从点出发，以每秒2个单位长度的速度沿线段匀速运动到点，再以每秒1个单位长度的速度沿线段匀速运动到点后停止运动，求点的运动时间的最小值．
【答案】（1）；（2），；（3）等腰直角三角形，理由见解析；（4）
【分析】
（1）根据已知条件，运用待定系数法直接列方程组求解即可；
（2）根据（1）中二次函数解析式，直接利用顶点坐标公式计算即可，再根据点A、B坐标求出AB解析式即可；
（3）根据二次函数对称性可知为等腰三角形，再根据O、A、B三点坐标，求出三条线段的长，利用勾股定理验证即可；
（4）根据题意可知动点的运动时间为，在上取点，使，可证明，根据相似三角形比例关系得，即，当、、三点共线时，取得最小值，再根据等腰直角三角形的性质以及勾股定理进一步计算即可．
【详解】
解：（1）二次函数的图象经过，且与轴交于原点及点
∴，二次函数表达式可设为：
将，代入得：
解这个方程组得
∵二次函数的函数表达式为
（2）∵点为二次函数图像的顶点，
∴，
∴顶点坐标为：，
设直线的函数表达式为，则有：
解之得：
∴直线的函数表达式为
（3）是等腰直角三角形，
过点作于点，易知其坐标为
∵的三个顶点分别是，，，
∴，
且满足
∴是等腰直角三角形
（4）如图，以为圆心，为半径作圆，则点在圆周上，依题意知：
动点的运动时间为
在上取点，使，
连接，则在和中，
满足：，，
∴，
∴，
从而得：
∴
显然当、、三点共线时，取得最小值，
过点作于点，由于，
且为等腰直角三角形，
则有，，
∴动点的运动时间的最小值为：
．
【点睛】
本题主要考查待定系数法求函数解析式，抛物线顶点坐标，等腰直角三角形的性质与判定，相似三角形的判定与性质等知识点，将运动时间的最小值转换为线段长度的最小值是解题的关键．
11.我们把方程（x﹣m）2+（y﹣n）2＝r2称为圆心为（m，n）、半径长为r的圆的标准方程．例如，圆心为（1，﹣2）、半径长为3的圆的标准方程是（x﹣1）2+（y+2）2＝9．在平面直角坐标系中，⊙C与轴交于点A，B，且点B的坐标为（8，0），与y轴相切于点D（0，4），过点A，B，D的抛物线的顶点为E．
（1）求⊙C的标准方程；
（2）试判断直线AE与⊙C的位置关系，并说明理由．
【分析】（1）如图，连接CD，CB，过点C作CM⊥AB于M．设⊙C的半径为r．在Rt△BCM中，利用勾股定理求出半径以及等C的坐标即可解决问题．
（2）结论：AE是⊙C的切线．连接AC，CE．求出抛物线的解析式，推出点E的坐标，求出AC，AE，CE，利用勾股定理的逆定理证明∠CAE＝90°即可解决问题．
【解析】（1）如图，连接CD，CB，过点C作CM⊥AB于M．设⊙C的半径为r．
∵与y轴相切于点D（0，4），
∴CD⊥OD，
∵∠CDO＝∠CMO＝∠DOM＝90°，
∴四边形ODCM是矩形，
∴CM＝OD＝4，CD＝OM＝r，
∵B（8，0），
∴OB＝8，
∴BM＝8﹣r，
在Rt△CMB中，∵BC2＝CM2+BM2，
∴r2＝42+（8﹣r）2，
解得r＝5，
∴C（5，4），
∴⊙C的标准方程为（x﹣5）2+（y﹣4）2＝25．
（2）结论：AE是⊙C的切线．
理由：连接AC，CE．
∵CM⊥AB，
∴AM＝BM＝3，
∴A（2，0），B（8，0）
设抛物线的解析式为y＝a（x﹣2）（x﹣8），
把D（0，4）代入y＝a（x﹣2）（x﹣8），可得a，
∴抛物线的解析式为y（x﹣2）（x﹣8）x2x+4（x﹣5）2，
∴抛物线的顶点E（5，），
∵AE，CE＝4，AC＝5，
∴EC2＝AC2+AE2，
∴∠CAE＝90°，
∴CA⊥AE，
∴AE是⊙C的切线．
12.如图，抛物线y＝ax2x+c经过点A（﹣1，0）和点C（0，3）与x轴的另一交点为点B，点M是直线BC上一动点，过点M作MP∥y轴，交抛物线于点P．
（1）求该抛物线的解析式；
（2）在抛物线上是否存在一点Q，使得△QCO是等边三角形？若存在，求出点Q的坐标；若不存在，请说明理由；
（3）以M为圆心，MP为半径作⊙M，当⊙M与坐标轴相切时，求出⊙M的半径．
【分析】（1）把点A（﹣1，0）和点C （0，3）代入y＝ax2x+c求出a与c的值即可得出抛物线的解析式；
（2）①当点Q在y轴右边时，假设△QCO为等边三角形，过点Q作QH⊥OC于H，OC＝3，则OH，tan60°，求出Q（，），把x代入yx2x+3，得y，则假设不成立；
②当点Q在y轴的左边时，假设△QCO为等边三角形，过点Q作QT⊥OC于T，OC＝3，则OT，tan60°，求出Q（，），把x代入yx2x+3，得y，则假设不成立；
（3）求出B（4，0），待定系数法得出BC直线的解析式yx+3，当M在线段BC上，⊙M与x轴相切时，延长PM交AB于点D，则点D为⊙M与x轴的切点，即PM＝MD，设P（x，x2x+3），M（x，x+3），则PDx2x+3，MDx+3，由PD﹣MD＝MD，求出x＝1，即可得出结果；当M在线段BC上，⊙M与y轴相切时，延长PM交AB于点D，过点M作ME⊥y轴于E，则点E为⊙M与y轴的切点，即PM＝ME，PD﹣MD＝EM＝x，设P（x，x2x+3），M（x，x+3），则PDx2x+3，MDx+3，代入即可得出结果；当M在BC延长线，⊙M与x轴相切时，点P与A重合，M的纵坐标的值即为所求；当M在CB延长线，⊙M与y轴相切时，延长PD交x轴于D，过点M作ME⊥y轴于E，则点E为⊙M与y轴的切点，即PM＝ME，PD﹣MD＝EM＝x，设P（x，x2x+3），M（x，x+3），则PDx2x﹣3，MDx﹣3，代入即可得出结果．
【解析】（1）把点A（﹣1，0）和点C （0，3）代入y＝ax2x+c得：，
解得：，
∴抛物线的解析式为：yx2x+3；
（2）不存在，理由如下：
①当点Q在y轴右边时，如图1所示：
假设△QCO为等边三角形，
过点Q作QH⊥OC于H，
∵点C （0，3），
∴OC＝3，
则OHOC，tan60°，
∴QH＝OH•tan60°，
∴Q（，），
把x代入yx2x+3，
得：y，
∴假设不成立，
∴当点Q在y轴右边时，不存在△QCO为等边三角形；
②当点Q在y轴的左边时，如图2所示：
假设△QCO为等边三角形，
过点Q作QT⊥OC于T，
∵点C （0，3），
∴OC＝3，
则OTOC，tan60°，
∴QT＝OT•tan60°，
∴Q（，），
把x代入yx2x+3，
得：y，
∴假设不成立，
∴当点Q在y轴左边时，不存在△QCO为等边三角形；
综上所述，在抛物线上不存在一点Q，使得△QCO是等边三角形；
（3）令x2x+3＝0，
解得：x1＝﹣1，x2＝4，
∴B（4，0），
设BC直线的解析式为：y＝kx+b，把B、C的坐标代入则，
解得：，
∴BC直线的解析式为：yx+3，
当M在线段BC上，⊙M与x轴相切时，如图3所示：
延长PM交AB于点D，
则点D为⊙M与x轴的切点，即PM＝MD，
设P（x，x2x+3），M（x，x+3），
则PDx2x+3，MDx+3，
∴（x2x+3）﹣（x+3）x+3，
解得：x1＝1，x2＝4（不合题意舍去），
∴⊙M的半径为：MD3；
当M在线段BC上，⊙M与y轴相切时，如图4所示：
延长PM交AB于点D，过点M作ME⊥y轴于E，
则点E为⊙M与y轴的切点，即PM＝ME，PD﹣MD＝EM＝x，
设P（x，x2x+3），M（x，x+3），
则PDx2x+3，MDx+3，
∴（x2x+3）﹣（x+3）＝x，
解得：x1，x2＝0（不合题意舍去），
∴⊙M的半径为：EM；
当M在BC延长线，⊙M与x轴相切时，如图5所示：
点P与A重合，
∴M的横坐标为﹣1，
∴⊙M的半径为：M的纵坐标的值，
即：（﹣1）+3；
当M在CB延长线，⊙M与y轴相切时，如图6所示：
延长PD交x轴于D，过点M作ME⊥y轴于E，
则点E为⊙M与y轴的切点，即PM＝ME，PD﹣MD＝EM＝x，
设P（x，x2x+3），M（x，x+3），
则PDx2x﹣3，MDx﹣3，
∴（x2x﹣3）﹣（x﹣3）＝x，
解得：x1，x2＝0（不合题意舍去），
∴⊙M的半径为：EM；
综上所述，⊙M的半径为或或或．
13.在平面直角坐标系中，二次函数y＝x2+bx+c的图象与x轴交于A(﹣2，0)，B(4，0)两点，交y轴于点C，点P是第四象限内抛物线上的一个动点．
（1）求二次函数的解析式；
（2）如图甲，连接AC，PA，PC，若，求点P的坐标；
（3）如图乙，过A，B，P三点作⊙M，过点P作PE⊥x轴，垂足为D，交⊙M于点E．点P在运动过程中线段DE的长是否变化，若有变化，求出DE的取值范围；若不变，求DE的长．
【答案】（1）y＝x2﹣x﹣4；（2）P(3，﹣)；（3）没有变化，2
【解析】
【分析】
（1）由二次函数的图象与轴交于，两点，可得二次函数的解析式为，由此即可解决问题．
（2）根据，构建方程即可解决问题．
（3）结论：点在运动过程中线段的长是定值，．根据，根据方程求出，再利用中点坐标公式，求出点的纵坐标即可解决问题．
【详解】
解：（1）二次函数的图象与轴交于，两点，
二次函数的解析式为，
即．
（2）如图甲中，连接．设．
由题意，，，
，
，
整理得，，
解得或（舍弃），
．
（3）结论：点在运动过程中线段的长是定值，．
理由：如图乙中，连接，，，设，，，．
由题意，，
，
解得，
，，
，
，
，
点在运动过程中线段的长是定值，．
【点睛】
本题属于二次函数综合题，考查了三角形的面积，三角形的外接圆，三角形的外心等知识，解题的关键是学会利用参数构建方程解决问题，属于中考压轴题．
14.如图，在直角坐标系中，四边形OABC是平行四边形，经过A（﹣2，0），B，C三点的抛物线y＝ax2+bx+（a＜0）与x轴的另一个交点为D，其顶点为M，对称轴与x轴交于点E．
（1）求这条抛物线对应的函数表达式；
（2）已知R是抛物线上的点，使得△ADR的面积是平行四边形OABC的面积的，求点R的坐标；
（3）已知P是抛物线对称轴上的点，满足在直线MD上存在唯一的点Q，使得∠PQE＝45°，求点P的坐标．
【答案】（1）y＝﹣x2+x+；（2）（1+，4）或（1﹣，4）或（1+，﹣4）或（1﹣，﹣4）；（3）P（1，120﹣168）
【解析】
【分析】
【详解】
解：（1）OA＝2＝BC，故函数的对称轴为x＝1，则x＝﹣＝1①，
将点A的坐标代入抛物线表达式得：0＝4a﹣2b+②，
联立①②并解得，故抛物线的表达式为：y＝﹣x2+x+③；
（2）由抛物线的表达式得，点M（1，3）、点D（4，0）；
∵△ADR的面积是▱OABC的面积的，
∴×AD×|yR|＝×OA×OB，则×6×|yR|＝×2×，解得：yR＝±④，
联立④③并解得，或
故点R的坐标为（1+，4）或（1﹣，4）或（1+，﹣4）或（1﹣，﹣4）；
（3）作△PEQ的外接圆R，
∵∠PQE＝45°，故∠PRE＝90°，
则△PRE为等腰直角三角形，
当直线MD上存在唯一的点Q，则RQ⊥MD，
点M、D的坐标分别为（1，4）、（4，0），
则ME＝4，ED＝4﹣1＝3，则MD＝5，
过点R作RH⊥ME于点H，
设点P（1，2m），则PH＝HE＝HR＝m，则圆R的半径为m，则点R（1+m，m），
S△MED＝S△MRD+S△MRE+S△DRE，即×EM•ED＝×MD×RQ+×ED•yR+×ME•RH，
∴×4×3＝×5×m+×4×m+×3×m，解得m＝60﹣84，故点P（1，120﹣168）．
15如图1，在平面直角坐标系中，，以O为圆心，OA的长为半径的半圆O交AO的延长线于C，连接AB，BC，过O作ED//BC分别交AB和半圆O于E，D，连接OB，CD．
（1）求证：BC是半圆O的切线；
（2）试判断四边形OBCD的形状，并说明理由；
（3）如图2，若抛物线经过点D，且顶点为E，求此抛物线的解析式；点P 是此抛物线对称轴上的一动点，以E，D，P为顶点的三角形与相似，问抛物线上是否存在点Q，使得，若存在，请直接写出Q点的横坐标；若不存在，说明理由．
【答案】（1）见解析；（2）平行四边形，见解析；（3）抛物线的解析式为，存在，Q点的横坐标为或或或
【解析】
【分析】
（1）证得OE是△ABC的中位线，求得点E的坐标，分别求得AB、AC、BC的长，利用勾股定理的逆定理证得是直角三角形，从而证明结论；
（2）求得BC=OD=OA=，利用平行四边形的判定定理可证得四边形OBCD是平行四边形；
（3）证明Rt△ODNRt△OEM，求得点D的坐标，利用待定系数法可求得此抛物线的解析式；分△PED△OAB和△DEP△OAB两种情况讨论，利用相似三角形的性质求得PE的长，再根据三角形的面积公式即可求得Q点的横坐标．
【详解】
（1）如图1，
设AB与y轴交于点M，则AM=2，OM=1，AB=5，
则OA=OC，
∵OE∥BC，
∴OE是△ABC的中位线，
∴AE=AB=，BC=2EO，
∴点E的坐标为(，)，ME=，OM=1，
∴OE=，
∴BC=2OE=，
∵，
是直角三角形，
即，
所以BC是半圆的O的切线；
（2）四边形OBCD是平行四边形，
由图知： BC=OD=OA=，
∵OD∥BC，
∴四边形OBCD是平行四边形；
（3）①由（2）知：OD=OA=，
E为AB的中点，过点D作轴，则DN//ME，
∴Rt△ODNRt△OEM，
∴，
∴，
∴，，
∴点D的坐标为(，)，
∵抛物线经过点D(，)，且顶点为E(，)，
∴设此抛物线的解析式为，
则
∴，
∴此抛物线的解析式为，
即，
如图，设抛物线对称轴交AC于F，
由（1）知：∠AOE=∠ACB=90，∠AEF=90，
∴∠OEF+∠AEO=90，∠A+∠AEO=90，
∴∠OEF=∠A，
∵以E，D，P为顶点的三角形与相似，
∴分△PED△OAB和△DEP△OAB两种情况讨论，
当△PED△OAB时，ED=OE+OD=
，即，
∴，
∵，
设点Q到PE的距离为h，
∴，即，
∴，
∴点Q的横坐标为或；
当△DEP△OAB时，ED=OE+OD=
，即，
∴，
∵，
设点Q到PE的距离为，
∴，即，
∴，
∴点Q的横坐标为或；
∴符合条件的Q点的横坐标为或或或．
【点睛】
本题是二次函数的综合题，考查了待定系数法求二次函数的解析式，圆的切线的判定，相似三角形的性质和判定，勾股定理的逆定理，平行四边形的判定等知识点的应用，此题综合性比较强，有一定的难度，对学生提出较高的要求．注意：不要漏解，分类讨论思想的巧妙运用．
16.如图，在平面直角坐标系中，直线与x轴交于点A，与y轴交于点B，抛物线过点B且与直线相交于另一点．
（1）求抛物线的解析式；
（2）点P是抛物线上的一动点，当时，求点P的坐标；
（3）点在x轴的正半轴上，点是y轴正半轴上的一动点，且满足．
①求m与n之间的函数关系式；
②当m在什么范围时，符合条件的N点的个数有2个？
【答案】（1）；（2）或（3，）或（-2，-3）；（3）①；②0＜m＜
【解析】
【分析】
（1）利用一次函数求出A和B的坐标，结合点C坐标，求出二次函数表达式；
（2）当点P在x轴上方时，点P与点C重合，当点P在x轴下方时，AP与y轴交于点Q，求出AQ表达式，联立二次函数，可得交点坐标，即为点P；
（3）①过点C作CD⊥x轴于点D，证明△MNO∽△NCD，可得，整理可得结果；
②作以MC为直径的圆E，根据圆E与线段OD的交点个数来判断M的位置，即可得到m的取值范围.
【详解】
解：（1）∵直线与x轴交于点A，与y轴交于点B，
令x=0，则y=2，令y=0，则x=4，
∴A（4，0），B（0，2），
∵抛物线经过B（0，2），，
∴，解得：，
∴抛物线的表达式为：；
（2）当点P在x轴上方时，点P与点C重合，满足，
∵，
∴，
当点P在x轴下方时，如图，AP与y轴交于点Q，
∵，
∴B，Q关于x轴对称，
∴Q（0，-2），又A（4，0），
设直线AQ的表达式为y=px+q，代入，
，解得：，
∴直线AQ的表达式为：，联立得：
，解得：x=3或-2，
∴点P的坐标为（3，）或（-2，-3），
综上，当时，点P的坐标为：或（3，）或（-2，-3）；
（3）①如图，∠MNC=90°，过点C作CD⊥x轴于点D，
∴∠MNO+∠CND=90°，
∵∠OMN+∠MNO=90°，
∴∠CND=∠OMN,又∠MON=∠CDN=90°，
∴△MNO∽△NCD，
∴，即，
整理得：；
②如图，∵∠MNC=90°，
以MC为直径画圆E，
∵，
∴点N在线段OD上（不含O和D），即圆E与线段OD有两个交点（不含O和D），
∵点M在y轴正半轴，
当圆E与线段OD相切时，
有NE=MC，即NE2=MC2，
∵M（0，m），，
∴E（，），
∴=，
解得：m=，
当点M与点O重合时，如图，
此时圆E与线段OD（不含O和D）有一个交点，
∴当0＜m＜时，圆E与线段OD有两个交点，
故m的取值范围是：0＜m＜.
【点睛】
本题是二次函数综合，考查了求二次函数表达式，相似三角形的判定和性质，圆周角定理，一次函数表达式，难度较大，解题时要充分理解题意，结合图像解决问题.
17.将抛物线向下平移6个单位长度得到抛物线，再将抛物线向左平移2个单位长度得到抛物线．

（1）直接写出抛物线，的解析式；
（2）如图（1），点在抛物线对称轴右侧上，点在对称轴上，是以为斜边的等腰直角三角形，求点的坐标；
（3）如图（2），直线（，为常数）与抛物线交于，两点，为线段的中点；直线与抛物线交于，两点，为线段的中点．求证：直线经过一个定点．
【答案】（1）抛物线的解析式为： y=x2-4x-2；抛物线的解析式为：y=x2-6；（2）点的坐标为（5，3）或（4，-2）；（3）直线经过定点（0，2）
【解析】
【分析】
（1）根据函数图象上下平移：函数值上加下减；左右平移：自变量左加右减写出函数解析式并化简即可；
（2）先判断出点A、B、O、D四点共圆，再根据同弧所对的圆周角相等得到∠BDA=∠BOA=45°，从而证出是等腰直角三角形．设点A的坐标为（x，x2-4x-2），把DC和AC用含x的代数式表示出来，利用DC=AC列方程求解即可，注意有两种情况；
（3）根据直线（，为常数）与抛物线交于，两点，联立两个解析式，得到关于x的一元二次方程，根据根与系数的关系求出点M的横坐标，进而求出纵坐标，同理求出点N的坐标，再用待定系数法求出直线MN的解析式，从而判断直线MN经过的定点即可．
【详解】
解：（1）∵抛物线向下平移6个单位长度得到抛物线，再将抛物线向左平移2个单位长度得到抛物线，
∴抛物线的解析式为：y=(x-2)2-6，即y=x2-4x-2，
抛物线的解析式为：y=(x-2+2)2-6，即y=x2-6．
（2）如下图，过点A作AC⊥x轴于点C，连接AD，
∵是等腰直角三角形，
∴∠BOA =45°，
又∵∠BDO=∠BAO=90°，
∴点A、B、O、D四点共圆，
∴∠BDA=∠BOA=45°，
∴∠ADC=90°-∠BDA=45°，
∴是等腰直角三角形，
∴DC=AC．
∵点在抛物线对称轴右侧上，点在对称轴上，
∴抛物线的对称轴为x=2，
设点A的坐标为（x，x2-4x-2），
∴DC=x-2，AC= x2-4x-2，
∴x-2= x2-4x-2，
解得：x=5或x=0（舍去），
∴点A的坐标为（5，3）；
同理，当点B、点A在x轴的下方时，
x-2= -(x2-4x-2)，
x=4或x=-1（舍去），
∴点的坐标为（4，-2），
综上，点的坐标为（5，3）或（4，-2）．
（3）∵直线（，为常数）与抛物线交于，两点，
∴，
∴x2-kx-6=0，
设点E的横坐标为xE，点F的横坐标为xF，
∴xE+xF=k，
∴中点M的横坐标xM==，
中点M的纵坐标yM=kx=，
∴点M的坐标为（，）；
同理可得：点N的坐标为（，），
设直线MN的解析式为y=ax+b（a≠0），
将M（，）、N（，）代入得：
，
解得：，
∴直线MN的解析式为y= ·x+2（），
不论k取何值时（），当x=0时，y=2，
∴直线经过定点（0，2）．
【点睛】
本题考查二次函数综合应用，熟练掌握图象平移的规律、判断点A、B、O、D四点共圆的方法、用待定系数法求函数解析式的步骤是解题的关键．
18.如图1，在平面直角坐标系中，点A的坐标是，在x轴上任取一点M．连接AM，分别以点A和点M为圆心，大于的长为半径作弧，两弧相交于G，H两点，作直线GH，过点M作x轴的垂线l交直线GH于点P．根据以上操作，完成下列问题．
探究：
（1）线段PA与PM的数量关系为________，其理由为：________________．
（2）在x轴上多次改变点M的位置，按上述作图方法得到相应点P的坐标，并完成下列表格：
猜想：
（3）请根据上述表格中P点的坐标，把这些点用平滑的曲线在图2中连接起来；观察画出的曲线L，猜想曲线L的形状是________．
验证：
（4）设点P的坐标是，根据图1中线段PA与PM的关系，求出y关于x的函数解析式．
应用：
（5）如图3，点，，点D为曲线L上任意一点，且，求点D的纵坐标的取值范围．
【答案】（1），线段垂直平分线上的点与这条线段两个端点的距离相等；（2）图见解析，抛物线；（3）见解析；（4）；（5）
【解析】
【分析】
（1）由尺规作图的步骤可知，HG是AM的中垂线，结合中垂线的性质，即可得到答案；
（2）根据第（1）的作图方法，得到相应点P的位置，即可求解；
（3）用平滑的曲线作出图象，即可；
（4）过点P作轴于点E，用含x，y的代数式表示，，，结合勾股定理，即可得到答案；
（5）连接，由题意得当时，在的外接圆上，弧所对的圆心角为60°，的外接圆圆心为坐标原点O，设，求出b的值，进而即可求解．
【详解】
解：（1） 线段垂直平分线上的点与这条线段两个端点的距离相等
（2）
（3）草图见图2：形状：抛物线
（4）如图1，过点P作轴于点E，
，，
在中，
即
化简，得
∴y关于x的函数解析式为．

（5）连接，易得，又
∴为等边三角形，∴
当时，在的外接圆上，弧所对的圆心角为60°
其圆心在的垂直平分线y轴上，
∴的外接圆圆心为坐标原点O，
设，则，即 ①
又点D在该抛物线上
∴ ②
由①②联立解得：（舍去）
数形结合可得，
当时，点D的纵坐标的取值范围为
【点睛】
本题主要考查尺规作作中垂线，二次函数的图象和性质，圆周角定理，解题关键是：熟练掌握垂直平分线的性质定理，构造三角形的外接圆．
19.如图，已知，是的平分线，是射线上一点，．动点从点出发，以的速度沿水平向左作匀速运动，与此同时，动点从点出发，也以的速度沿竖直向上作匀速运动．连接，交于点．经过、、三点作圆，交于点，连接、．设运动时间为，其中．
（1）求的值；
（2）是否存在实数，使得线段的长度最大？若存在，求出的值；若不存在，说明理由．
（3）求四边形的面积．
【答案】（1）8cm；（2）存在，当t=4时，线段OB的长度最大，最大为；（3）
【解析】
【分析】
（1）根据题意可得，，由此可求得的值；
（2）过作，垂足为，则，设线段的长为，可得，，，根据可得，进而可得，由此可得，由此可得，则可得到答案；
（3）先证明是等腰直角三角形，由此可得，再利用勾股定理可得，最后根据四边形的面积即可求得答案．
【详解】
解：（1）由题可得：，．
∴．
（2）当时，线段的长度最大．
如图，过作，垂足为，则．
∵平分，
∴，
∴，．
设线段的长为，
则，，．
∵，
∴，
∴，
∴，
解得：．
∴．
∴当时，线段的长度最大，最大为．
（3）∵，
∴是圆的直径．
∴．
∵，
∴是等腰直角三角形．
∴
．
在中，．
∴四边形的面积
．
∴四边形的面积为．
【点睛】
本题考查了相似三角形的判定及性质，直径的判定及性质，二次函数的最值问题等相关知识，熟练掌握相关知识是解决本题的关键．
20如图，抛物线y＝ax2+x+c经过点A（﹣1，0）和点C （0，3）与x轴的另一交点为点B，点M是直线BC上一动点，过点M作MP∥y轴，交抛物线于点P．
（1）求该抛物线的解析式；
（2）在抛物线上是否存在一点Q，使得△QCO是等边三角形？若存在，求出点Q的坐标；若不存在，请说明理由；
（3）以M为圆心，MP为半径作⊙M，当⊙M与坐标轴相切时，求出⊙M的半径．
【答案】（1）y＝﹣x2+x+3；（2）不存在，理由见解析；（3）⊙M的半径为，，，
【解析】
【分析】
（1）已知抛物线y＝ax2+x+c经过点A(﹣1,0)和点C(0,3)，利用待定系数法即可求得抛物线解析式；
（2）在抛物线上找到一点Q，使得△QCO是等边三角形，过点Q作OM⊥OB于点M，过点Q作QN⊥OC于点N，根据△QCO是等边三角形，求得Q点坐标，再验证Q点是否在抛物线上；
（3）分四种情况①当⊙M与y轴相切，如图所示，令M点横坐标为t，PM=t，将PM用t表示出来，列出关于t的一元二次方程，求得t，进而求得半径；②⊙M与x轴相切，过点M作MN⊥OB于N，如图所示，令M点横坐标为m，因为PN=2MN，列出关于m的一元二次方程，即可求出m，同理③④种情况，进而求得⊙M的半径．
【详解】
（1）∵抛物线y＝ax2+x+c经过点A(﹣1,0)和点C(0,3)
∴
解得
∴该抛物线的解析式为：y＝﹣x2+x+3
故答案为：y＝﹣x2+x+3
（2）在抛物线上找到一点Q，使得△QCO是等边三角形，过点Q作OM⊥OB于点M，过点Q作QN⊥OC于点N
∵△QCO是等边三角形，OC=3
∴CN=
∴NQ=
即Q(,)
当x=时，y＝﹣×()2+×+3=≠
∴Q(,)不在抛物线上
y＝﹣x2+x+3
故答案为：不存在，理由见解析
（3）①⊙M与y轴相切，如图所示
∵y＝﹣x2+x+3
当y=0时，﹣x2+x+3=0
解得x1=-1，x2=4
∴B(4,0)
令直线BC的解析式为y=kx+b
解得
∴直线BC的解析式为
令M点横坐标为t
∵MP∥y轴，⊙M与y轴相切
∴t=﹣t2+t+3-
解得t=
⊙M的半径为
②⊙M与x轴相切，过点M作MN⊥OB于N，如图所示
令M点横坐标为m
∵PN=2MN
∴
解得m=1或m=4（舍去）
∴⊙M的半径为：
③当与轴相切时，如图3：
点与点重合时
半径
④当与轴相切时如图4：
设，
则，因
解得，（舍去）
半径
综上所述：的半径为，，，
【点睛】
本题考查了待定系数法求二次函数解析式，是二次函数的综合题，涉及了二次函数与几何问题，二次函数与圆的问题，其中考查了圆切线的性质．
21.我们把方程(x- m)2+(y-n)2=r2称为圆心为(m，n)、半径长为r的圆的标准方程．例如，圆心为(1,-2)、半径长为3的圆的标准方程是(x- 1)2+(y+2)2=9．在平面直角坐标系中,圆C与轴交于点A．B．且点B的坐标为(8．0),与y轴相切于点D(0, 4)，过点A,B,D的抛物线的顶点为E．
(1)求圆C的标准方程；
(2)试判断直线AE与圆C的位置关系，并说明理由．
【答案】（1）；（2）相切，理由见解析
【解析】
【分析】
（1）连接CD，CB，过C作CF⊥AB，分别表示出BF和CF，再在△BCF中利用勾股定理构造方程求解即可得到圆C半径以及点C坐标，从而得到标准方程；
（2）由（1）可得点A坐标，求出抛物线表达式，得到点E坐标，再求出直线AE的表达式，联立直线AE和圆C的表达式，通过判断方程根的个数即可得到两者交点个数，从而判断位置关系.
【详解】
解：连接CD，CB，过C作CF⊥AB，
∵点D（0，4），B（8，0），设圆C半径为r，圆C与y轴切于点D，
则CD=BC=OF=r，CF=4，
∵CF⊥AB，
∴AF=BF=8-r，
在△BCF中，，
即，
解得：r=5，
∴CD=OF=5，即C（5，4），
∴圆C的标准方程为：；
（2）由（1）可得：BF=3=AF，则OA=OB-AB=2，
即A（2，0），
设抛物线表达式为：，将A，B，D坐标代入，
，解得：，
∴抛物线表达式为：，
∴可得点E（5，），
设直线AE表达式为：y=mx+n，将A和E代入，
可得：，解得：，
∴直线AE的表达式为：，
∵圆C的标准方程为，
联立，
解得：x=2，
故圆C与直线AE只有一个交点，横坐标为2，
即圆C与直线AE相切.
【点睛】
本题考查了圆的新定义，二次函数，一次函数，切线的判定，垂径定理，有一定难度，解题的关键是利用转化思想，将求位置关系转化为方程根的个数问题.
x
…
0
1
2
3
…
y
…
0
3
4
3
0
…
M的坐标
…
…
P的坐标
…
…
M的坐标
…
…
P的坐标
…
…