2024年春安徽省九年级中考数学模拟试题2（含答案）

这是一份2024年春安徽省九年级中考数学模拟试题2（含答案），共13页。试卷主要包含了 单选题， 填空题， 解答题等内容，欢迎下载使用。

一、 单选题 （本题共计10小题，总分40分）
1.（4分）-4的倒数是( )
A.-4B.−14C.14D.4
2.（4分）一个如图所示的几何体,已知它的左视图,则其俯视图是下面的( )
A.B.C.D.
3.（4分）下列计算正确的是( )
A.b3+b3=b6B.b3⋅b3=b9C.(b3)3=b9D.b6÷b3=b2
4.（4分）不等式组{1−3x≤73x<−15的解集在数轴上表示正确的是( )
A.B.C.D.
5.（4分）下列函数中,y的值随x值增大而增大的是( )
A.y=3x2+1B.y=−3x2+1C.y=3x+1D.y=−3x+1
6.（4分）如图,在平行四边形ABCD中,BA=BD,∠AEB=90°,若∠C=70°,则∠DAE=( )
A.10°B.20°C.30°D.40°
7.（4分）在一个不透明的盒子中,装有10个除颜色外其他均相可的小球.已知从袋中任意摸出一球是白球的概率为15,若将这一事件的概率提升至13,则需要增加白球的个数为( )
A.2B.3C.4D.5
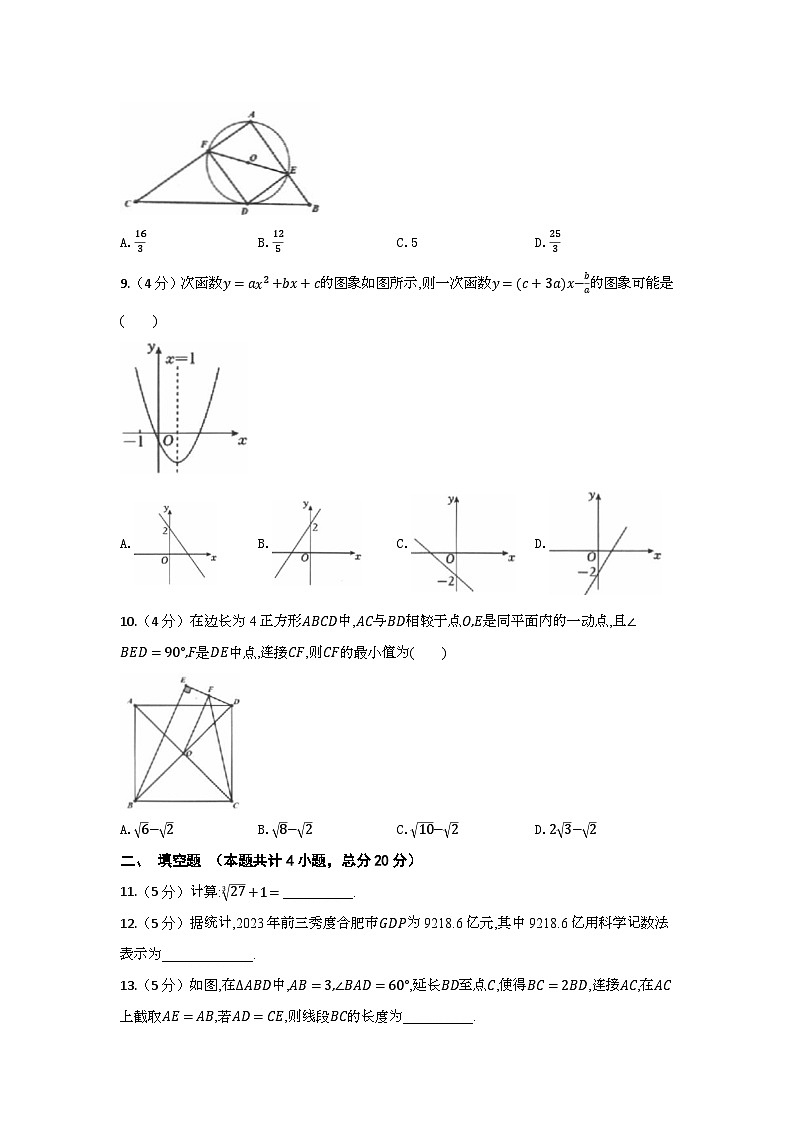
8.（4分）如图,在直角三角形ABC中,∠A=90°,E,F分別是AB,AC上两点,以EF为直径作圆与BC相切于点D,且DE⊥AB,DF⊥AC.若BD=4,BE=3,则AB的长度为( )
A.163B.125C.5D.253
9.（4分）次函数y=ax2+bx+c的图象如图所示,则一次函数y=(c+3a)x−ba的图象可能是( )
A.B.C.D.
10.（4分）在边长为4正方形ABCD中,AC与BD相较于点O,E是同平面内的一动点,且∠BED=90°,F是DE中点,连接CF,则CF的最小值为( )
A.6−2B.8−2C.10−2D.23−2
二、 填空题 （本题共计4小题，总分20分）
11.（5分）计算:327+1=__________.
12.（5分）据统计,2023年前三秀度合肥市GDP为9218.6亿元,其中9218.6亿用科学记数法表示为_____________.
13.（5分）如图,在ΔABD中,AB=3,∠BAD=60°,延长BD至点C,使得BC=2BD,连接AC,在AC上截取AE=AB,若AD=CE,则线段BC的长度为__________.
14.（5分）在同一平面内,直线y=kx+1与抛物线y=14x2交于A、B两点,设A(x1,y1),B(x2,y2).
(1)x1⋅x2=___________;
(2)若点N(0,−1),且AN与BN不垂直,则k的取值范国是:___________.
三、 解答题 （本题共计9小题，总分90分）
15.（8分）先化简,再求值:(x+1x−1)÷x2−1x2+x,其中x=−2.
16.（8分）《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.其中《盈不足》卷记载了道数学问题:“今有共买物,人出六,赢二;人出五,不足三.问人数、物价各几何?"译文:“今有人合伙购物,每人出6钱,会多出2钱:每人出5钱,又差3钱.问人数、物价各多少?”请解答上述问题.
17.（8分）如图,在平面直角坐标系中,单位长度为1,ΔABC的顶点均在正方形网格的格点上,其中A(0,1).
(1)画出ΔABC关于原点对称的图形ΔA1B1C1;
(2)写出顶点C1的坐标;
(3)用无刻度的直尺画出AC的中点M.
18.（8分）如图,用5个实心圆圈,5个空心圆圈相间组成一个圆环,然后把这样的圆环从左到右按下列规律组成圆环串;相邻两圆坏有一公共圆圈,公共圆圈从左到有以实心圆圈和空心埙腃相问排列.
(1)把下列表格补充完整:
(2)设圆环中由x个圆环组成,请你古接写出组成这圆环所需实心圆淃和空心圆圈的总个数个(用含x的代数式表示):
(3)如果圆环串成这样的圆环18个组成,那么实心圆圈和空心圆圈的总数有多少个?有多少个空心圆图？
19.（10分）为建设美好公园社区,增强民众生活幸福感,某社区服务中心在文化活动室墙外安装遮阳篷,使于社区居民休想在如图的侧面示意图中,遮阳篷靠墙端离地高记为BC,遮阳篷AB长为5米,与水平面的夹角为16°.
(1)求点A到墙面BC的距离:
(2)当太阳光线AD与地面CE的夹角为45°时,量得影长CD为1.8米,求遮阳篷靠墙端离地高BC的长.(结果精确到0.1米;参考数据:sin16°≈0.28,cs16°≈0.96,tan16°≈0.29)
20.（10分）如图,在四边形ABCD中,AO平分∠BAD.点O在AC上,以点O为圆心,OA为半径,作⨀O与BC相切于点B,BO延长线交⨀O于点E,交AD于点F,连接AE,DE.
(1)求证:CD是⨀O的切线:
(2)若AE=DE=8,求AF的长.
21.（12分）合肥市在创建全国文明城市期间,某中学九年级开展创文明知识竞赛活动,并随机抽取部分学牛成绩作为样木进行分析,绘制成如下的统计表:
九年级抽取部分学生成续的频率分布表
请根据所给信息,解答下列问题:
(1)本次总共调查的人数是________人:
(2)表中a=_______,b=_________:将右侧频数分布图补充完整
(3)已知该校九年级共有500名学生参加这次竞赛,月成绩在90分以上的成绩为优秀,估计该年级竞赛成绩为优秀的学生共有多少人?
22.（12分）在ΔABC和ΔADE中,AB=AC=5,AD=AE=6,且∠BAC=∠DAE,sin∠BAD=0.8.
(1)如图,当∠BAC=60°时,连接DC,并延长DC交AE于点F,则DF=___________;
(2)当∠BAC=90°时,求H1CD的长;
(3)当∠BAC满足什么条件时,四边形ABDC是菱形.
23.（14分）在平面直角坐标系xOy中,已知抛物线y=a(x+1)(x−4)与x轴交于A、B两点,与y轴交于点C(0,−2).
(1)求a的值;
(2)点D为第四象限抛物线上一点
①求ΔBCD的面积最大值
②连接AD,BC交于点E,连接BD,记ΔBDE的面积为S1,ΔABE的面积为S2,求S1S2的最大值;
答案
一、 单选题 （本题共计10小题，总分40分）
1.（4分）【答案】B
2.（4分）【答案】A
3.（4分）【答案】C
4.（4分）【答案】D
5.（4分）【答案】C
6.（4分）【答案】B
7.（4分）【答案】A
8.（4分）【答案】A
9.（4分）【答案】B
10.（4分）【答案】C
二、 填空题 （本题共计4小题，总分20分）
11.（5分）【答案】4
12.（5分）【答案】9.2186×1011
13.（5分）【答案】213
14.（5分）(1)−4;
【解析】解:由题意得x1,x2满足方程14x2−kx−1=0;y1,y2满足方程y2−(2+4k2)y+1=0.依据根与系数的关系得,x1+x2=4k,x1⋅x2=−4
(2)k≠0
【解析】由题意,kAN=y1+1x1,kBN=y2+1x2,
∴kAN⋅kBN=y1+1x1⋅y2+1x2=(y1+1)(y2+1)x1x2=4k2+2+1+1−4=−k2−1.
∴当k=0时,AN⊥BN;当k≠0时,AN与BN不垂直.
三、 解答题 （本题共计9小题，总分90分）
15.（8分）【答案】解:(x+1x−1)÷x2−1x2+x
=x+1−xx⋅x(x+1)(x+1)(x−1)
=1x⋅xx−1
=1x−1,
当x=−2时,原式=1−2−1=−13.
16.（8分）【答案】解:设共x人合伙购物,物价是y钱,
依题意得:{6x−y=2y−5x=3,
解得:{x=5y=28.
答:共5人合伙购物,物价是28钱.
17.（8分）(1)解:如图,ΔA1B1C1即为所求;
(2)顶点C1的坐标为(−4,−4);
(3)如图，点M即为所求。
18.（8分）(1)解:37,46,55;
(2)设圆环串由x个圆环组成，组成这圆环所需实心圆圈和空心圆圈的总个数为9x+1;
故答案为:(9x+1);
(3)当x=18时,实心圆圈和空心圆圈的总个数为9×18+1=163,
因为围成偶数个圆环需要的实心圆圈比空心圆圈多1个,
所以需要82个实心圆圈,需要81个空心圆圈.
答:实心圆圈和空心圆圈的总数有163个,有81个空心圆圈.
19.（10分）(1)解:过点A作AF⊥BC,垂足为F,
在RtΔABF中,AB=5米,∠BAF=16°,
∴AF=AB⋅cs16°≈5×0.96=4.8(米),
∴点A到墙面BC的距离约为4.8米;
(2)过点A作AG⊥CE,垂足为G,
由题意得:AG=CF,AF=CG=4.8米,
∵CD=1.8米,
∴DG=CG−CD=4.8−1.8=3(米),.
在RtΔADG中,∠ADG=45°,
∴AG=DG⋅tan45°=3(米),
∴CF=AG=3米,
在RtΔABF中,AB=5米,∠BAF=16°,
∴BF=AB⋅sin16°≈5×0.28=1.4(米),
∴BC=BF+CF=1.4+3=4.4(米),
∴遮阳篷靠墙端离地高BC的长为4.4米.
20.（10分）(1)证明:如图,连接OD.
∵BC为圆O的切线
∴∠CBO=90°.
∵AO平分∠BAD,
∴∠OAB=∠OAF.
∵OA=OB=OD,
∴∠OAB=∠ABO=∠OAF=∠ODA,
∵∠BOC=∠OAB+∠OBA,∠DOC=∠OAD+∠ODA,
∴∠BOC=∠DOC,
在ΔCOB和ΔCOD中,
{CO=CO∠COB=∠CODOB=OD
∴ΔBOC≅ΔDOC,
∴∠CBO=∠CDO=90°,
∴CD是⨀O的切线;
(2)∵AE=DE,
∴
∴∠DAE=∠ABO,
∴∠BAO=∠OAD=∠ABO
∴∠BAO=∠OAD=∠DAE,
∵BE是直径,
∴∠BAE=90°,
∴∠BAO=∠OAD=∠DAE=∠ABO=30°,
∴∠AFE=90°,
在RtΔAFE中,
∵AE=10,∠DAE=30°,
∴EF=12AE=4,
∴AF=AE2−EF2=82−42=43.
21.（12分）(1)解:2÷0.04=50,
答:本次总共调查的人数是50;
故答案为:50;
(2)a=50×0.36=18,b=14÷50=0.28,
补全频数分布直方图如下:
(3)500×(0.36+0.28)=320(人)
22.（12分）(1)解:∵AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴ΔABC和ΔADE是等边三角形,
∴AB=BC,AD=DE
∵ΔABD≅ΔACE
∴BC=CE
∴点D、C在AE的中垂线上,
∴CD是AE的中垂线,
∵点F在DC的延长线上,
∴DF⊥AE,AF=EF,
∴AF=EF=3,AD=6,
∴DF=AD2−AF2=62−32=33,
(2)依据题意作图如图1,过点E作BE⊥AD于点E,过点C作CF⊥AD于点F,连接CD,
∵AB=5,BE⊥AD,
∴BE=0.8AB=4,
在RtΔABE中,AB=5,BE=4,
∴AE=AB−BE2=3,
∵∠CAB=90°,
∴∠CAF+∠EAB=90°,
∵CF⊥AD,
∴∠CAF+∠ACF=90°,
∴∠EAB=∠ACF,
∵BE⊥AD,CF⊥AD,
∴∠BEA=∠AFC=90°,
∴ΔACF≅ΔBEA(AAS),
∴FA=BE=4,AE=CF=3,
∴DF=AD−AF=6−4=2,
则CD=DF2+CF2=22+32=13;
(3)当∠BAC=2∠BAD时,四边形AEBC为菱形,理由如下:
由前面可知:AB=BD=5,∠BDA=∠BAD
当∠BAC=2∠BAD时,∠BDA=∠CAD∴AC//BD,
∵AC=BD,∴四边形ABDC为平行四边形，
∵AC=AB,∴平行四边形ABDC为菱形.
23.（14分）(1)解:将C(0,−2)代入得:4a=2,解得a=12,
∴抛物线的解析式为y=12(x+1)(x−4),即y=12x2−32x−2.
(2)①过点D作DM⊥x轴于点N,交BC于点M
设直线BC的解析式为y=kx+b,
∴{4k+b=0b=−2,解得{k=12b=−2,
∴直线BC的解析式为y=12x−2,
设点D(a,12a2−32a−2),则点M(a,12a−2)0SΔBCD=SΔBMD+SΔCMD
=12DM⋅xB
=12×4(−12a2+2a)
=−a2+4a
∴当a=2吋,面积最大,最大值为4
②过点D作DG⊥x轴于点G,交BC于点F,过点A作AK⊥x轴交BC的延长线于点K.
∴AK//DG,
∴ΔAKE∼ΔDFE,
∴DFAK=DEAE,
∴S1S2=SΔBDESΔABE=DEAE=DFAK,
∵A(−1,0),
∴y=−12−2=−52,
∴AK=52,
设D(m,12m2−32m−2),则F(m,12m−2),
∴DF=12m−2−12m2+32m+2=−12m2+2m.
∴S1S2=−12m2+2m52=−15m2+45m=−15(m−2)2+45.
∴当m=2时,S1S2有最大值,最大值是45.