2023-2024学年福建省福州市闽侯县八年级（下）期中数学试卷（含解析）

这是一份2023-2024学年福建省福州市闽侯县八年级（下）期中数学试卷（含解析），共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．要使代数式有意义，则x的取值范围是（ ）
A．x≥2B．x≠2C．x＞2D．x≤2
2．下列计算正确的是（ ）
A．B．C．D．
3．如图，A，B两地被池塘隔开，小明先在AB外选一点C，然后测出AC，BC的中点M，N，若MN的长为16米，则A，B间的距离是（ ）
A．18米B．20米C．24米D．32米
4．在平行四边形ABCD中，∠A+∠C＝100°，则∠B的度数为（ ）
A．50°B．80°C．100°D．130°
5．下列条件中，a，b，c分别为三角形的三边，不能判断△ABC为直角三角形的是（ ）
A．a2＝b2+c2B．a＝8，b＝15，c＝17
C．a＝9，b＝16，c＝18D．
6．四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（ ）
A．AB∥DC，AD∥BCB．AB＝DC，AD＝BC
C．AO＝CO，BO＝DOD．AB＝DC，AD∥BC
7．如图，两平行线l1和l2之间的距离是4，点A，D在l1上，点B在l2上，且∠BAD＝135°，则AB的长为（ ）
A．B．C．4D．8
8．在平面直角坐标系中，平行四边形ABCD的顶点A，B，C的坐标分别是（0，0），（5，0），（2，3），则顶点D的坐标是（ ）
A．（﹣3，3）B．（3，﹣3）C．（7，3）D．（﹣5，3）
9．已知点E，F，G，H分别在正方形ABCD的边AB，BC，CD，DA上，若EG∥BC，FH∥CD，则四边形EFGH一定是（ ）
A．矩形
B．菱形
C．正方形
D．对角线互相垂直且相等的四边形
10．如图，当秋千静止时，踏板离地的垂直高度BE＝0.5m，将它往前推1.2m至C处时（即水平距离CD＝1.2m），踏板离地的垂直高度CF＝1.1m，它的绳索始终拉直，则绳索AC的长是（ ）
A．1.5mB．1.6mC．1.8mD．2m
二、填空题（共6小题，每题4分，满分24分）
11．化简＝ ．
12．已知一个菱形的面积为10cm2，它其中一条对角线的长度为10cm，则另一条对角线的长度为 cm．
13．在Rt△ABC中，∠ABC＝90°，点O是斜边AC的中点，若AB＝6，BC＝8，则OB的长度为 ．
14．如图，矩形ABCD的两条对角线相交于点O，若∠AOD＝60°，AD＝3，则AC的长为 ．
15．已知n是正整数，是整数，则n的最小值是 ．
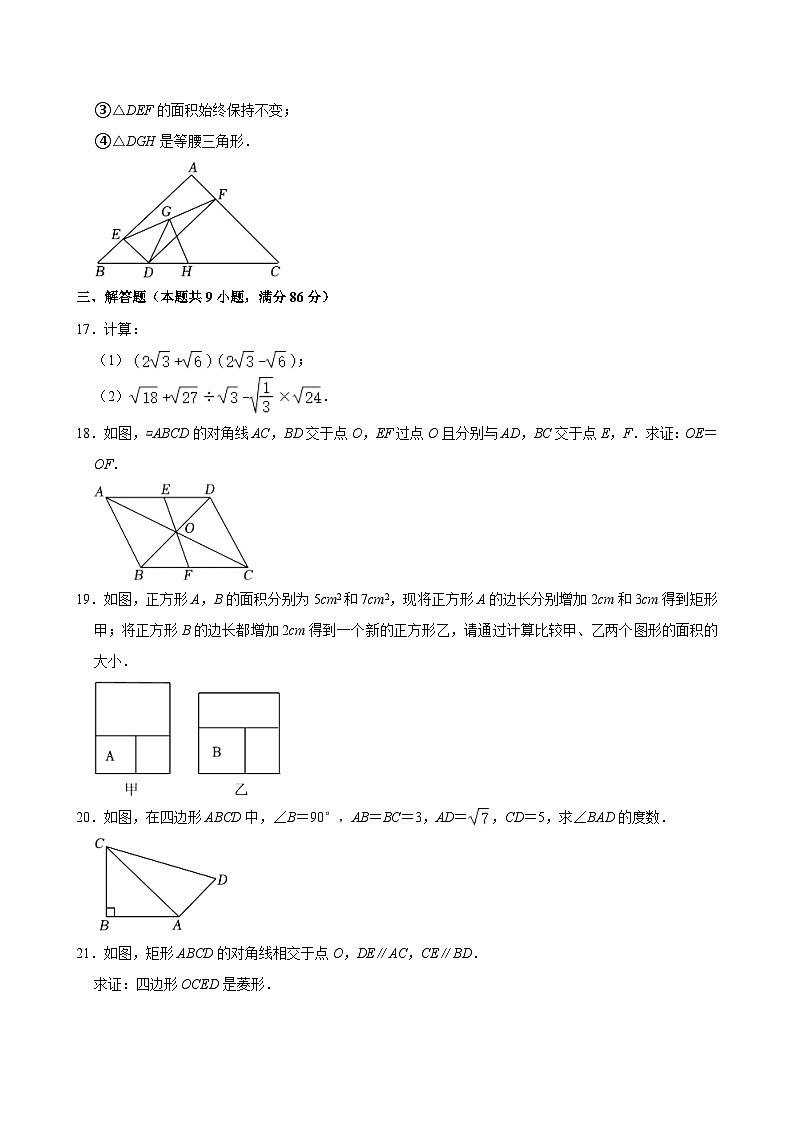
16．如图，△ABC是等腰直角三角形，∠A＝90°，点D在线段BC上，过D作DE⊥AB于E，DF⊥AC于F，点G，H分别是EF，BC的中点，若AB＝4，则下列结论正确的是 .（写出所有正确结论的序号）
①；
②EF的最小值是；
③△DEF的面积始终保持不变；
④△DGH是等腰三角形．
三、解答题（本题共9小题，满分86分）
17．计算：
（1）；
（2）．
18．如图，▱ABCD的对角线AC，BD交于点O，EF过点O且分别与AD，BC交于点E，F．求证：OE＝OF．
19．如图，正方形A，B的面积分别为5cm2和7cm2，现将正方形A的边长分别增加2cm和3cm得到矩形甲；将正方形B的边长都增加2cm得到一个新的正方形乙，请通过计算比较甲、乙两个图形的面积的大小．
20．如图，在四边形ABCD中，∠B＝90°，AB＝BC＝3，AD＝，CD＝5，求∠BAD的度数．
21．如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD．
求证：四边形OCED是菱形．
22．如图，在△ABC中，∠C＝90°．
（1）尺规作图：在AC边上找出点D，使得BD+CD＝AC；（不写作法，保留作图痕迹）
（2）在（1）条件下，连接BD，若AC＝2BC＝8，求BD的长．
23．如图，点E在正方形ABCD的边BC上，∠AEF＝90°且EF＝AE，过点F作FM⊥BC，垂足为M．
（1）求证：BE＝CM；
（2）延长CD至点N，使得DN＝BE，求证：四边形AEFN是正方形．
24．如1，在平面直角坐标系xOy中，矩形OABC的顶点O，A和C的坐标分别为O（0，0），A（0，a），C（c，0），且a，c满足．
（1）求a，c的值；
（2）点D在OC上，将△OAD沿AD折叠，使点O落在矩形内点E处．
①如图2，D，E，B三点共线，连接BE，求此时点D的坐标；
②如图3，若点D是线段OC的中点，连接CE，求CE的长．
25．如图1，E是正方形ABCD外一点，且满足∠BED＝90°，连接CE．
（1）求证：CE平分∠BED；
（2）如图2，连接AE，求证：；
（3）如图3，M是BE的中点，作DN⊥CE于点N，连接AM，MN，求证：AM⊥MN．
参考答案
一、选择题（共10小题，每小题4分，满分40分，每小题只有一个正确的选项，请在答题卡的相应位置填涂）
1．要使代数式有意义，则x的取值范围是（ ）
A．x≥2B．x≠2C．x＞2D．x≤2
【分析】根据二次根式有意义的条件列不等式求解．
解：由题意可得x﹣2≥0，
解得x≥2，
故选：A．
【点评】本题考查二次根式有意义的条件，理解二次根式有意义的条件（被开方数为非负数）是解题关键．
2．下列计算正确的是（ ）
A．B．C．D．
【分析】根据二次根式的加减运算法则逐项判断即可．
解：A、和不是同类二次根式，无法合并，故本选项错误，不符合题意；
B、，故本选项错误，不符合题意；
C、，故本选项正确，符合题意；
D、2和不是同类二次根式，无法合并，故本选项错误，不符合题意；
故选：C．
【点评】本题主要考查了二次根式的加减运算，二次根式相加减，先把各个二次根式化成最简二次根式，再把被开方数相同的二次根式进行合并，合并方法为系数相加减，根式不变．
3．如图，A，B两地被池塘隔开，小明先在AB外选一点C，然后测出AC，BC的中点M，N，若MN的长为16米，则A，B间的距离是（ ）
A．18米B．20米C．24米D．32米
【分析】根据题意，MN是△ABC的中位线，由此即可求解．
解：根据题意，MN是△ABC的中位线，
∴AB＝2MN＝2×16＝32（米），
故选：D．
【点评】本题主要考查三角形中位线的运用，理解并掌握中位线的性质是解题的关键．
4．在平行四边形ABCD中，∠A+∠C＝100°，则∠B的度数为（ ）
A．50°B．80°C．100°D．130°
【分析】根据平行四边形的对角相等、邻角互补以及图形可知∠A与∠C是对角，即可求出∠A和∠C的度数；再根据∠B与∠A是邻角，即可求得∠B．
解：如图：
∵四边形ABCD为平行四边形，
∴∠A+∠B＝180°，∠A＝∠C．
∵∠A+∠C＝100°，
∴∠A＝50°，
∴∠B＝130°．
故选：D．
【点评】本题主要考查了平行四边形的性质，熟练掌握平行四边形的性质是解题的关键．
5．下列条件中，a，b，c分别为三角形的三边，不能判断△ABC为直角三角形的是（ ）
A．a2＝b2+c2B．a＝8，b＝15，c＝17
C．a＝9，b＝16，c＝18D．
【分析】根据勾股定理的逆定理，逐项判断即可求解．
解：A、a2＝b2+c2，能判断△ABC为直角三角形，故本选项不符合题意；
B、82+152＝172，能判断△ABC为直角三角形，故本选项不符合题意；
C、92+162≠182，不能判断△ABC为直角三角形，故本选项符合题意；
D、设，则，能判断△ABC为直角三角形，故本选项不符合题意；
故选：C．
【点评】本题主要考查了勾股定理的逆定理，熟练掌握勾股定理及其逆定理是解答本题的关键．
6．四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（ ）
A．AB∥DC，AD∥BCB．AB＝DC，AD＝BC
C．AO＝CO，BO＝DOD．AB＝DC，AD∥BC
【分析】分别利用平行四边形的判定方法进行判断，即可得出结论．
解：∵AB∥DC，AD∥BC，
∴四边形ABCD是平行四边形，故选项A不合题意；
∵AB＝CD，AD＝BC，
∴四边形ABCD是平行四边形，故选项B不合题意；
∵AO＝CO，BO＝DO，
∴四边形ABCD是平行四边形，故选项C不合题意；
∵AB＝CD，AD∥BC，
∴四边形ABCD不一定是平行四边形，故选项D符合题意；
故选：D．
【点评】本题考查了平行四边形的判定，掌握平行四边形的判定方法是本题的关键．
7．如图，两平行线l1和l2之间的距离是4，点A，D在l1上，点B在l2上，且∠BAD＝135°，则AB的长为（ ）
A．B．C．4D．8
【分析】如图：过A作AC⊥l2，根据平行线的性质可得∠ABC＝45°、AC＝4，进而说明∠BAC＝∠ABC＝45°，根据等角对等边可得BC＝AC＝4，最后根据勾股定理即可解答即可．
解：如图：过A作AC⊥l2，
∵两平行线l1和l2之间的距离是4，∠BAD＝135°，
∴∠ABC＝180°﹣∠BAD＝45°，AC＝4，
∵AC⊥l2，
∴∠BAC＝∠ABC＝45°，
∴BC＝AC＝4，
∴．
故选：B．
【点评】本题主要考查了平行线的性质、等腰三角形的性质、勾股定理等知识点，掌握等腰三角形的性质成为解题的关键．
8．在平面直角坐标系中，平行四边形ABCD的顶点A，B，C的坐标分别是（0，0），（5，0），（2，3），则顶点D的坐标是（ ）
A．（﹣3，3）B．（3，﹣3）C．（7，3）D．（﹣5，3）
【分析】如图：根据平行四边形对边平行且相等的性质可得AB∥DC，AB＝DC，进而确定点C和点D纵坐标相同，再根据两点之间的距离列方程即可解答．
解：根据题意，作图如下，
∵平行四边形ABCD，
∴AB∥DC，AB＝DC，
∴DC∥x轴，
∴点C和点D纵坐标相同，即为3；
又∵AB＝DC，点C（2，3），
∴2﹣5＝﹣3，
∴点D坐标为（﹣3，3）．
故选：A．
【点评】本题主要考查图形与坐标和平行四边形的性质，灵活运用平行四边形的性质成为解题的关键．
9．已知点E，F，G，H分别在正方形ABCD的边AB，BC，CD，DA上，若EG∥BC，FH∥CD，则四边形EFGH一定是（ ）
A．矩形
B．菱形
C．正方形
D．对角线互相垂直且相等的四边形
【分析】根据正方形的性质可得∠BCD＝90°、BC＝CD，再根据平行线的性质可得∠CGE＝∠BCD＝90°、EG＝BC、∠EOF＝∠EGC＝90°、FH＝CD，进而得到结论．
解：∵正方形ABCD，
∴∠BCD＝90°，BC＝CD
∵EG∥BC，
∴∠CGE＝∠BCD＝90°，EG＝BC，
∵FH∥CD，
∴∠EOF＝∠EGC＝90°，FH＝CD，
∴EG⊥FH
∵BC＝CD，
∴FH＝EG，即四边形EFGH一定是对角线互相垂直且相等的四边形．
故选：D．
【点评】本题主要考查了正方形的性质、平行线的性质等知识点，掌握正方形的性质成为解题的关键．
10．如图，当秋千静止时，踏板离地的垂直高度BE＝0.5m，将它往前推1.2m至C处时（即水平距离CD＝1.2m），踏板离地的垂直高度CF＝1.1m，它的绳索始终拉直，则绳索AC的长是（ ）
A．1.5mB．1.6mC．1.8mD．2m
【分析】根据提议可得四边形CFDE是矩形，由此得DE＝CF＝1.1m，进而可得DB＝0.6m．绳索长x m，则AB长x m，AD长（x﹣0.6）m，在Rt△ACD中，根据勾股定理列方程求出x的值即可．
解：由题意得∠DEF＝∠CFE＝∠CDE＝90°，
∴四边形CFDE是矩形，
∴DE＝CF＝1.1m，
∵BE＝0.5m，
∴DB＝1.1﹣0.5＝0.6（m）．
设绳索长x m，则AB长x m，AD长（x﹣0.6）m，
在Rt△ACD中，根据勾股定理得AC2＝AD2+CD2，
∴x2＝（x﹣0.6）2+1.22，
解得x＝1.5，
∴AC＝1.5，
故选：A．
【点评】本题主要考查了矩形的性质和勾股定理，熟练掌握以上知识是解题的关键．
二、填空题（共6小题，每题4分，满分24分）
11．化简＝ 2024 ．
【分析】当a≥0时，；当a＜0时，，据此计算即可．
解：，
故答案为：2024．
【点评】本题考查了二次根式的性质与化简，属于基础题．
12．已知一个菱形的面积为10cm2，它其中一条对角线的长度为10cm，则另一条对角线的长度为 2 cm．
【分析】设另一条对角线长为x cm，由菱形的面积公式计算，即可求解．
解：设另一条对角线长为x cm，由菱形的面积公式得：
，
解得x＝2，
即另一条对角线的长为2cm．
故答案为：2．
【点评】本题主要考查了求菱形的面积，解答本题的关键是熟练掌握菱形的性质．
13．在Rt△ABC中，∠ABC＝90°，点O是斜边AC的中点，若AB＝6，BC＝8，则OB的长度为 5 ．
【分析】先根据勾股定理求得AC，然后根据直角三角形斜边上的中线等于斜边的一半即可解答．
解：∵在Rt△ABC中，AB＝6，BC＝8，
∴，
∵点O是斜边AC的中点，
∴．
故答案为：5．
【点评】本题主要考查了勾股定理、直角三角形的性质等知识点，掌握直角三角形斜边上的中线等于斜边的一半成为解题的关键．
14．如图，矩形ABCD的两条对角线相交于点O，若∠AOD＝60°，AD＝3，则AC的长为 6 ．
【分析】根据矩形的对角线互相平分且相等可得OC＝OD，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠OCD＝30°，然后根据直角三角形30°角所对的直角边等于斜边的一半解答．
解：在矩形ABCD中，OC＝OD，
∴∠OCD＝∠ODC，
∵∠AOD＝60°，
∴∠OCD＝∠AOD＝×60°＝30°，
又∵∠ADC＝90°，
∴AC＝2AD＝2×3＝6．
故答案为：6．
【点评】本题考查了矩形的性质，主要利用了矩形的对角线互相平分且相等的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记各性质是解题的关键．
15．已知n是正整数，是整数，则n的最小值是 35 ．
【分析】根据题意可变形为，即可求解．
解：∵，是整数，n是正整数，
∴n的最小值为35．
故答案为：35．
【点评】本题主要考查了二次根式的化简，关键是掌握二次根式的变形．
16．如图，△ABC是等腰直角三角形，∠A＝90°，点D在线段BC上，过D作DE⊥AB于E，DF⊥AC于F，点G，H分别是EF，BC的中点，若AB＝4，则下列结论正确的是 ①④ .（写出所有正确结论的序号）
①；
②EF的最小值是；
③△DEF的面积始终保持不变；
④△DGH是等腰三角形．
【分析】由∠BAC＝90°，AB＝AC，得∠B＝∠C＝45°，由∠BED＝∠CFD＝90°，得∠EDB＝∠B＝∠C＝∠FDC＝45°，则∠EDF＝90°，所以DG＝EF，可判断①正确；连接AD、AH，因为BC＝4，所以AH＝BH＝CH＝2，由AD≥AH，得AD≥2，再证明四边形AEDF是矩形，则AD＝EF，所以EF≥2，则EF的最小值为2，可判断②错误；可求得S△DEF＝BE（4﹣BE）＝﹣（BE﹣2）2+2，可知S△DEF的大小随BE的变化而变化，可判断③错误；连接FH、EH，可证明△HAF≌△HBE，得∠AHF＝∠BHE，推导出∠EHF＝∠AHB＝90°，则HG＝EF，所以DG＝HG，可判断④正确，于是得到问题的答案．
解：∵△ABC是等腰直角三角形，∠BAC＝90°，
∴AB＝AC，
∴∠B＝∠C＝45°，
∵DE⊥AB于E，DF⊥AC于F，
∴∠BED＝∠CFD＝90°，
∴∠EDB＝∠B＝∠C＝∠FDC＝45°，
∴∠EDF＝180°﹣∠EDB﹣∠FDC＝90°，
∵点G是EF的中点，
∴DG＝EF，
故①正确；
连接AD、AH，
∵∠BAC＝90°，AB＝AC＝4，点H是BC的中点，
∴BC＝＝4，AH⊥BC，BH＝CH，
∴AH＝BH＝CH＝BC＝2，
∵AD≥AH，
∴AD≥2，
∵∠AED＝∠AFD＝∠EDF＝90°，
∴四边形AEDF是矩形，
∴AD＝EF，
∴EF≥2，
∴EF的最小值为2，
故②错误；
∵∠EDF＝90°，BE＝DE，DF＝AE＝4﹣BE，
∴S△DEF＝DE•DF＝BE（4﹣BE）＝﹣（BE﹣2）2+2，
∴S△DEF的大小随BE的变化而变化，
故③错误；
连接FH、EH，
∵∠HAF＝∠HAB＝∠BAC＝45°，
∴∠HAF＝∠B，
∵AF＝DE，BE＝DE，
∴AF＝BE，
在△HAF和△HBE中，
，
∴△HAF≌△HBE（SAS），
∴∠AHF＝∠BHE，
∴∠EHF＝∠AHF+∠AHE＝∠BHE+∠AHE＝∠AHB＝90°，
∴HG＝EF，
∴DG＝HG，
∴△DGH是等腰三角形，
故④正确，
故答案为：①④．
【点评】此题重点考查等腰直角三角形的判定与性质、直角三角形斜边上的中线等于斜边的一半、勾股定理、全等三角形的判定与性质、等腰三角形的判定等知识，正确地作出辅助线是解题的关键．
三、解答题（本题共9小题，满分86分）
17．计算：
（1）；
（2）．
【分析】（1）先根据平方差公式计算，然后再运用二次根式的混合运算法则计算即可；
（2）直接运用二次根式的混合运算法则计算即可．
解：（1）
＝
＝12﹣6
＝6．
（2）
＝
＝
＝．
【点评】本题主要考查了二次根式的混合运算、平方差公式的知识点，灵活运用二次根式的混合运算法则成为解题的关键．
18．如图，▱ABCD的对角线AC，BD交于点O，EF过点O且分别与AD，BC交于点E，F．求证：OE＝OF．
【分析】要证明线段相等，只需证明两条线段所在的两个三角形全等即可．
【解答】证明：∵四边形ABCD是平行四边形，
∴AD∥BC，OA＝OC，
∴∠EAO＝∠FCO，
在△AOE和△COF中，
，
∴△AOE≌△COF（ASA），
∴OE＝OF．
【点评】此题考查了平行四边形的性质以及全等三角形的判定与性质．注意证得△AOE≌△COF是关键．
19．如图，正方形A，B的面积分别为5cm2和7cm2，现将正方形A的边长分别增加2cm和3cm得到矩形甲；将正方形B的边长都增加2cm得到一个新的正方形乙，请通过计算比较甲、乙两个图形的面积的大小．
【分析】根据题意表示出矩形甲和乙的面积，然后相减得到，然后由进而求解即可．
解：∵正方形A，B的面积分别为5cm2和7cm2，
∴正方形A，B的边长分别为和，
根据题意得，矩形甲的面积为：；
矩形乙的面积为：；
∴
＝
＝，
∵112＜125，
∴，
∴，
∴矩形甲的面积小于矩形乙的面积．
【点评】此题考查了二次根式混合运算的应用，根据题意表示出矩形甲和乙的面积是关键．
20．如图，在四边形ABCD中，∠B＝90°，AB＝BC＝3，AD＝，CD＝5，求∠BAD的度数．
【分析】先根据等腰三角形的性质及已知条件可得∠BAC＝∠BCA＝45°，再根据勾股定理可得AC2＝18，然后根据勾股定理逆定理可知∠CAD＝90°，最后根据角的和差即可解答．
解：∵∠B＝90°，AB＝BC＝3，
∴，AC2＝AB2+BC2＝32+32＝18，
∵，
∴AD2＝7，CD2＝25，
∴AD2+AC2＝CD2，即∠CAD＝90°，
∴∠BAD＝∠BAC+∠CAD＝45°+90°＝135°．
【点评】本题主要考查了等腰三角形的性质、勾股定理、勾股定理逆定理等知识点，灵活运用勾股定理相关知识成为解题的关键．
21．如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD．
求证：四边形OCED是菱形．
【分析】首先根据两对边互相平行的四边形是平行四边形证明四边形OCED是平行四边形，再根据矩形的性质可得OC＝OD，即可利用一组邻边相等的平行四边形是菱形判定出结论．
【解答】证明：∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形，
∵四边形ABCD是矩形，
∴OC＝OD，
∴四边形OCED是菱形．
【点评】此题主要考查了菱形的判定，矩形的性质，关键是掌握菱形的判定方法：①菱形定义：一组邻边相等的平行四边形是菱形；②四条边都相等的四边形是菱形；③对角线互相垂直的平行四边形是菱形．
22．如图，在△ABC中，∠C＝90°．
（1）尺规作图：在AC边上找出点D，使得BD+CD＝AC；（不写作法，保留作图痕迹）
（2）在（1）条件下，连接BD，若AC＝2BC＝8，求BD的长．
【分析】（1）根据线段垂直平分线的性质，作线段AB的垂直平分线，交AC于点D，则点D即为所求．
（2）设BD＝AD＝x，则CD＝8﹣x．在Rt△BCD中，由勾股定理得，BD2＝CD2+BC2，即x2＝（8﹣x）2+42，求出x的值，即可得出答案．
解：（1）如图，作线段AB的垂直平分线，交AC于点D，
则AD＝BD，
∴AC＝AD+CD＝BD+CD，
则点D即为所求．
（2）∵AC＝2BC＝8，
∴BC＝4．
设BD＝AD＝x，
则CD＝8﹣x．
在Rt△BCD中，由勾股定理得，BD2＝CD2+BC2，
即x2＝（8﹣x）2+42，
解得x＝5，
∴BD的长为5．
【点评】本题考查作图—复杂作图、线段垂直平分线的性质、勾股定理，熟练掌握线段垂直平分线的性质、勾股定理是解答本题的关键．
23．如图，点E在正方形ABCD的边BC上，∠AEF＝90°且EF＝AE，过点F作FM⊥BC，垂足为M．
（1）求证：BE＝CM；
（2）延长CD至点N，使得DN＝BE，求证：四边形AEFN是正方形．
【分析】（1）先根据正方形的性质以及已知条件证明△ABE≌△EMF（AAS）可得BC＝EM，然后根据线段的和差即可解答；
（2）先证明△ABE≌△ADN（SAS）可得AE＝AN，再证明AN∥EF可得四边形AEFN是平行四边形，再结合AE＝EF、∠AEF＝90°即可证明结论．
【解答】证明：（1）∵正方形ABCD，
∴∠B＝90°，AB＝BC，
∴∠BAE+∠BEA＝90°，
∵∠AEF＝90°，
∴∠BEA+∠FEM＝90°，∠AEF＝∠B，
∴∠BAE＝∠FEM，
∵EF＝AE
∴△ABE≌△EMF（AAS），
∴AB＝EM，
∴BC＝EM
∴BC﹣EC＝EM﹣EC，即BE＝CM．
（2）∵正方形ABCD，
∴∠B＝∠ADN＝90°，AB＝AD，
∵DN＝BE，
∴△ABE≌△ADN（SAS），
∴AE＝AN，∠BAE＝∠DAN，
∵AE＝EF
∴EF＝AN，
∵∠DAN+∠EAD＝∠BAE+∠EAD＝90°，
∴∠EAN＝∠AEF＝90°，
∴AN∥EF，
∴四边形AEFN是平行四边形，
∵AE＝EF，
∴四边形AEFN是菱形，
∵∠AEF＝90°，
∴四边形AEFN是正方形．
【点评】本题主要考查了正方形的性质、全等三角形的判定与性质、正方形的判定等知识点，灵活运用相关性质定理成为解题的关键．
24．如1，在平面直角坐标系xOy中，矩形OABC的顶点O，A和C的坐标分别为O（0，0），A（0，a），C（c，0），且a，c满足．
（1）求a，c的值；
（2）点D在OC上，将△OAD沿AD折叠，使点O落在矩形内点E处．
①如图2，D，E，B三点共线，连接BE，求此时点D的坐标；
②如图3，若点D是线段OC的中点，连接CE，求CE的长．
【分析】（1）根据算术平方根以及平方的非负性，列式计算，即可作答．
（2）先由折叠得出△OAD≌△EAD，①根据矩形性质以及等角对等边，得出BD＝AB＝6，再结合勾股定理列式计算，即可作答．
（3）通过斜边上的中线等于斜边的一半，得出∠OEC＝90°，再根据等面积法求出，然后结合勾股定理列式计算，即可作答．
解：（1）∵a，c满足．
∴，
则，
∴a＝4，b＝6；
（2）△OAD沿AD折叠，使点O落在矩形内点E，
∴△OAD≌△EAD，
①∵四边形OABC是矩形，且a＝4，b＝6，
∴OA＝BC＝4，OC＝AB＝6，AB∥OC，
∴∠BAD＝∠ODA，
∵△OAD≌△EAD，
∴∠ADE＝∠ODA，
∴∠BAD＝∠ADE，
即BD＝AB＝6，
在Rt△BCD中，，
∴，
即点D的坐标为；
②连接OE，交AD于点H，如图3，
∵D是线段OC的中点，
∴OD＝DC＝3，，
∵折叠，
∴DE＝OD＝DC，，
∴∠1＝∠2，∠3＝∠4，∠OEC＝∠2+∠3，
∵∠1+∠2+∠3+∠4＝180°，
∴，
∵，
∴，
即，
在Rt△OCE中，．
【点评】本题考查了矩形与折叠问题，勾股定理，坐标与图形，算术平方根的非负性，正确掌握相关性质内容是解题的关键．
25．如图1，E是正方形ABCD外一点，且满足∠BED＝90°，连接CE．
（1）求证：CE平分∠BED；
（2）如图2，连接AE，求证：；
（3）如图3，M是BE的中点，作DN⊥CE于点N，连接AM，MN，求证：AM⊥MN．
【分析】（1）如图所示，过点C作CF⊥BE于F，CG⊥ED交ED延长线于G，证明四边形CFEG是矩形得到∠FCG＝90°，再证明△BCF≌△DCG（AAS），得到CF＝CG，即可证明四边形CFEG是正方形，进而可证明结论；
（2）如图所示，过点D作DE⊥DH交CE于H，可证明△EDH是等腰直角三角形，得到ED＝HD，证明△ADE≌△CDH（SAS），得到AE＝CH，由勾股定理得，据此可证明；
（3）如图所示，延长NM到H，使得NM＝HM，连接AH，BH，AN，证明△HMB≌△NME（SAS），得到BH＝EN，∠MBH＝∠MEN，证明△DEN是等腰直角三角形，得到DN＝EN＝BH，进而证明△ABH≌△ADN（SAS），得到AH＝AN，由HM＝NM，可证明AM⊥MN．
【解答】证明：（1）如图1所示，过点C作CF⊥BE于F，CG⊥ED交ED延长线于G，
∵CF⊥BE，CG⊥ED，∠BED＝90°，
∴四边形CFEG是矩形，∠CFB＝∠CGD＝90°，
∴∠FCG＝90°，
∵四边形ABCD是正方形，
∴BC＝DC，∠BCD＝90°，
∴∠BCF＝∠DCG，
∴△BCF≌△DCG（AAS），
∴CF＝CG，
∴四边形CFEG是正方形，
∴∠CEF＝∠CEG＝45°，
∴CE平分∠BED；
（2）如图2所示，过点D作DE⊥DH交CE于H，
由（1）得∠CED＝45°，
∴△EDH是等腰直角三角形，
∴ED＝HD，
∵四边形ABCD是正方形，
∴DA＝DC，∠ADC＝∠EDH＝90°，
∴∠ADE＝∠CDH，
∴△ADE≌△CDH（SAS），
∴AE＝CH，
在Rt△EDH中，由勾股定理得，
∵CE＝CH+EH，
∴；
（3）如图3所示，延长NM到H，使得NM＝HM，连接AH，BH，AN，
∵M是BE的中点，
∴ME＝MB，
又∵NM＝HM，∠HMB＝∠NME，
∴△HMB≌△NME（SAS），
∴BH＝EN，∠MBH＝∠MEN，
∴BH∥CE，
∴∠CBH+∠BCE＝180°，
∴∠ABH+∠ABC+∠BCD﹣∠DCE＝180°，
∵∠ABC＝∠BCD＝90°，
∴∠ABH＝∠DCE，
∵DN⊥CE，
∴∠DCE+∠CDN＝90°＝∠CDN+∠ADN，
∴∠DCE＝∠ADN，
∴∠ADN＝∠ABH，
由（1）得∠DEN＝45°，
∴△DEN是等腰直角三角形，
∴DN＝EN＝BH，
又∵AD＝AB，
∴△ABH≌△ADN（SAS），
∴AH＝AN，
又∵HM＝NM，
∴AM⊥MN．
【点评】本题主要考查了正方形的性质与判定，全等三角形的性质与判定，等腰直角三角形的性质与判定，勾股定理，作出适当辅助线，构建全等三角形是解答本题的关键．