




2024年浙江省宁波市中考数学模拟试题(原卷版+解析版)
展开1. 春节期间冰雪旅游大热,杭州的小明同学准备去旅游,考虑温差准备着装时,他查询气温,结果如图所示,杭州的气温是,哈尔滨的气温是,则此刻两地的温差是( )
A. B. C. D.
2. 光年是天文学上的一种距离单位,一光年指光在一年内走过的路程,约等于km,数可以用科学记数法表示为( )
A B. C. D.
3. 下列计算正确的是( )
A. B. C. D.
4. 实数,在数轴上对应点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
5. 如图,已知,它们依次交直线于点A、B、C和点D、E、F,如果,那么的长等于( )
A. 2B. 4C. D.
6. 一组数据3、4、4、5,若添加一个数4后得到一组新数据,则前后两组数据的统计量会发生变化的是( )
A. 平均数B. 众数C. 中位数D. 方差
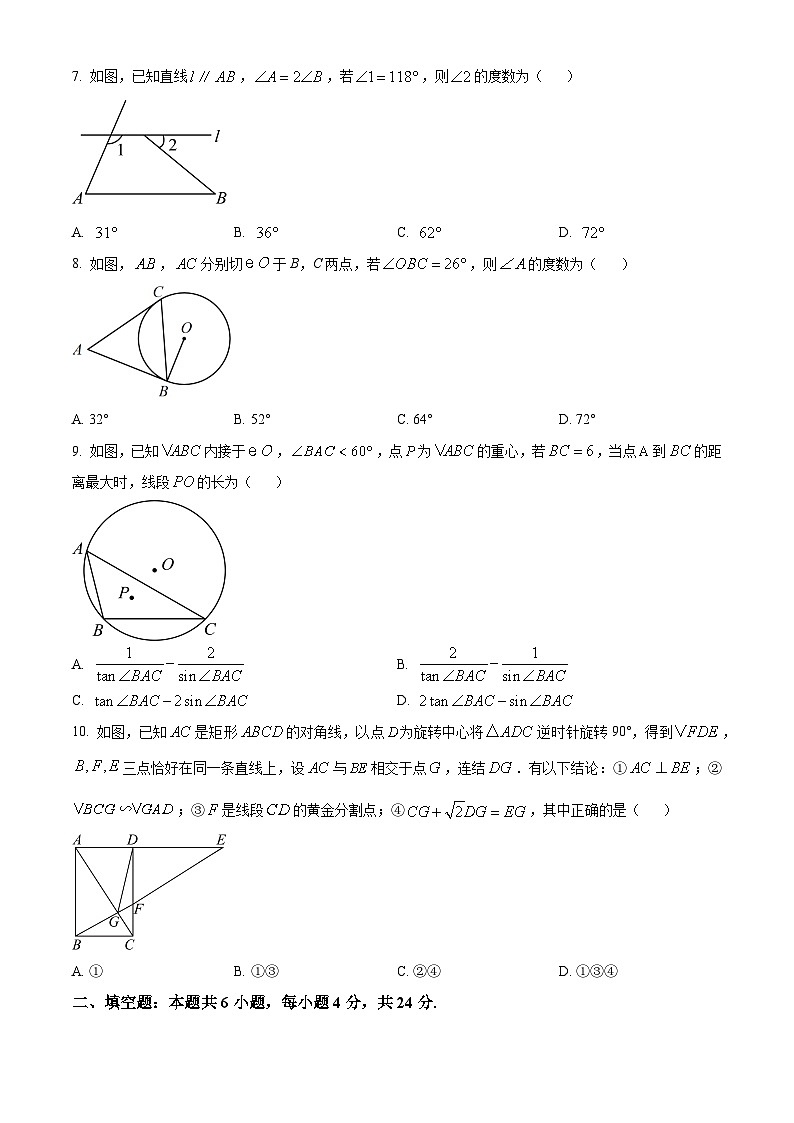
7. 如图,已知直线,,若,则的度数为( )
A. B. C. D.
8. 如图,,分别切于B,C两点,若,则的度数为( )
A. 32°B. 52°C. 64°D. 72°
9. 如图,已知内接于,,点为的重心,若,当点到的距离最大时,线段的长为( )
A. B.
C. D.
10. 如图,已知是矩形的对角线,以点为旋转中心将逆时针旋转90°,得到,三点恰好在同一条直线上,设与相交于点,连结.有以下结论:①;②;③是线段的黄金分割点;④,其中正确的是( )
A. ①B. ①③C. ②④D. ①③④
二、填空题:本题共6小题,每小题4分,共24分.
11. 分解因式:=_________________________.
12. 已知二次根式的值为4,则___________.
13. 不透明的袋子里有2个红球和1个白球,这些球除颜色外无其他差别,随机摸取两个球,恰好为一个红球一个白球的概率是_______________.
14. 若,则_______________.
15. 已知二次函数的图象与轴交于,两点,且满足.当时,则该函数的最大值与满足的关系式是______.
16. 如图,矩形中,,点为上一点,将沿着AE翻折得到,连结.若,且,则的长为______,的长为______.
三、解答题:本题共8小题,共66分.解答应写出文字说明,证明过程或演算步骤.
17. 计算6÷(﹣),方方同学的计算过程如下,原式=6÷(-)+6÷=﹣12+18=6.请你判断方方的计算过程是否正确,若不正确,请你写出正确的计算过程.
18. 端午节是中国的传统节日,民间有端午节吃粽子的习俗,在端午节来临之际,某校七、八年级开展了一次“包粽子”实践活动,对学生的活动情况按分制进行评分,成绩(单位:分)均为不低于的整数、为了解这次活动的效果,现从这两个年级各随机抽取名学生的活动成绩作为样本进行活整理,并绘制统计图表,部分信息如下:
八年级名学生活动成绩统计表
已知八年级名学生活动成绩的中位数为分.
请根据以上信息,完成下列问题:
(1)样本中,七年级活动成绩为分的学生数是______________,七年级活动成绩的众数为______________分;
(2)______________,______________;
(3)若认定活动成绩不低于分为“优秀”,根据样本数据,判断本次活动中优秀率高的年级是否平均成绩也高,并说明理由.
19. 如图,点是的边上一点,与边相切于点,与边、分别相交于点、,且.
(1)求证:;
(2)当,时,求的长.
20. 已知反比例函数,点都在该反比例函数图象上.
(1)求的值;
(2)若点都在该反比例函数图象上;
①当,点和点关于原点中心对称时,求点坐标;
②当时,求取值范围.
21. 《海岛算经》是中国古代测量术的代表作,原名《重差》.这本著作建立起了从直接测量向间接测量的桥梁.直至近代,重差测量法仍有借鉴意义.
如图,为测量海岛上一座山峰的高度,直立两根高2米的标杆和,两杆间距相距6米,D、B、H三点共线.从点B处退行到点F,观察山顶A,发现A、C、F三点共线,且仰角为;从点D处退行到点G,观察山顶A,发现A、E、G三点共线,且仰角为.(点F、G都在直线上)
(1)求的长(结果保留根号);
(2)山峰高度的长(结果精确到米).
(参考数据:,)
22. 某个农场有一个花卉大棚,是利用部分墙体建造的.其横截面顶部为抛物线型,大棚的一端固定在墙体上,另一端固定在墙体上,其横截面有根支架,,相关数据如图所示,其中支架,,这个大棚用了根支架.
为增加棚内空间,农场决定将图中棚顶向上调整,支架总数不变,对应支架的长度变化,如图所示,调整后与上升相同的高度,增加的支架单价为元/米(接口忽略不计),需要增加经费元.
(1)分别以和所在的直线为x轴和y轴建立平面直角坐标系.
①求出改造前的函数解析式.
②当米,求的长度.
(2)只考虑经费情况下,求出的最大值.
23 综合与实践
问题情境:
“综合与实践”课上,老师提出如下问题:如图1,在正方形中,是对角线上的动点(与点,不重合),连结,过点作,,分别交直线于点,.请说明,并求的值.
数学思考:
(1)请你解答老师提出的问题.
深入探究:
(2)如图2,老师将图1中的“正方形”改为“矩形”,其他条件均不变,并让同学们提出新的问题.
①“聪聪小组”提出问题:如图2,当,时,求的值;进一步,当时,直线写出的值(用含的代数式表示).
②“慧慧小组”提出问题:如图3,连结,当,,时,求的长.
请解答这两个问题:
24. 如图,,是两条直径,,点是上一点,连接,,分别交,于点,,连接,,.
(1)若,求的度数.
(2)求证:.
(3)设,的面积为,的面积为,求证:.成绩/分
人数
2024年浙江省宁波市初中学业水平考试数学模拟预测题(原卷版+解析版): 这是一份2024年浙江省宁波市初中学业水平考试数学模拟预测题(原卷版+解析版),共33页。
2024年浙江省宁波市镇海蛟川书院九年级中考第二次模拟数学模拟试题(原卷版+解析版): 这是一份2024年浙江省宁波市镇海蛟川书院九年级中考第二次模拟数学模拟试题(原卷版+解析版),文件包含2024年浙江省宁波市镇海蛟川书院九年级中考第二次模拟数学模拟试题原卷版docx、2024年浙江省宁波市镇海蛟川书院九年级中考第二次模拟数学模拟试题解析版docx等2份试卷配套教学资源,其中试卷共43页, 欢迎下载使用。
2024年浙江省宁波市中考数学模拟预测题(二)(原卷版+解析版): 这是一份2024年浙江省宁波市中考数学模拟预测题(二)(原卷版+解析版),文件包含2024年浙江省宁波市中考数学模拟预测题二原卷版docx、2024年浙江省宁波市中考数学模拟预测题二解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。












