广东省中山市纪中集团2023-2024学年七年级下学期期中数学试题（原卷版+解析版）

这是一份广东省中山市纪中集团2023-2024学年七年级下学期期中数学试题（原卷版+解析版），文件包含广东省中山市纪中集团2023-2024学年七年级下学期期中数学试题原卷版docx、广东省中山市纪中集团2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共20页， 欢迎下载使用。
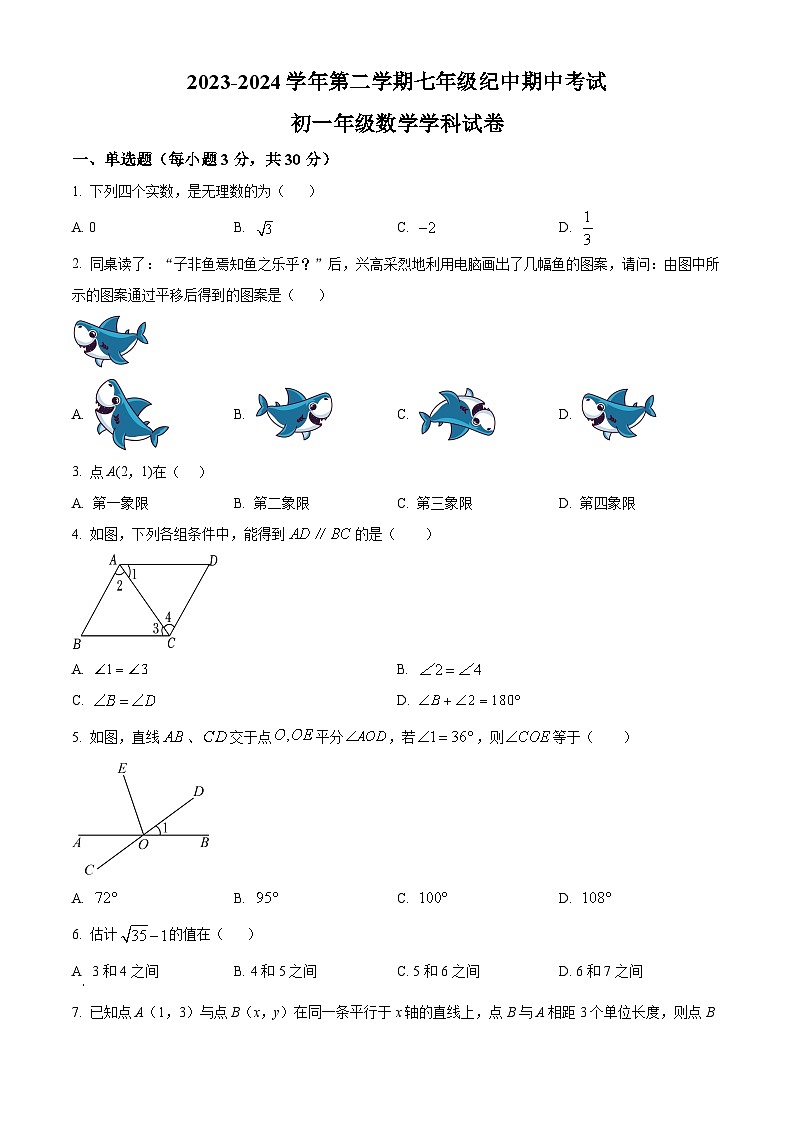
一、单选题（每小题3分，共30分）
1. 下列四个实数，是无理数为（ ）
A. 0B. C. D.
【答案】B
【解析】
【分析】根据无理数的定义逐一进行判断即可．
本题主要考查了无理数的定义，实数分为有理数和无理数，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，无限不循环小数为无理数，本题中带根号且开不尽的是无理数．
【详解】A. 0是有理数，故A选项不符合题意；
B. 是无理数，故B选项符合题意；
C. 是有理数，故C选项不符合题意；
D. 是有理数，故D选项不符合题意．
故选：B．
2. 同桌读了：“子非鱼焉知鱼之乐乎？”后，兴高采烈地利用电脑画出了几幅鱼的图案，请问：由图中所示的图案通过平移后得到的图案是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了平移的性质，根据平移不改变图形的形状和大小，只是位置发生变化，掌握平移的性质是解题的关键．
【详解】解：A、由图中所示的图案通过旋转而成，故本项错误；
B、由图中所示的图案通过翻折而成，故本项错误；
C、由图中所示的图案通过旋转而成，故本项错误；
D、由图中所示的图案通过平移而成，故本项正确；
故选：D．
3. 点A(2，1)在（ ）
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
【答案】A
【解析】
【分析】根据点的横、纵坐标均大于0即可得．
【详解】解：点的横坐标为，纵坐标为，
点在第一象限，
故选：A．
【点睛】本题考查了点所在的象限，熟练掌握平面直角坐标系中，各象限内的点的坐标的符号规律是解题关键．
4. 如图，下列各组条件中，能得到的是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】本题主要考查了平行线的判定，熟知平行线的判定条件是解题的关键．
【详解】解：A、，可以根据内错角相等，两直线平行得到，符合题意；
B、，可以根据内错角相等，两直线平行得到，不可以得到，不符合题意；
C、，不可以得到，不符合题意；
D、，不可以得到，不符合题意；
故选：A．
5. 如图，直线、交于点平分，若，则等于（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查的是邻补角的概念、角平分线的定义．根据邻补角的概念求出，根据角平分线的定义求出，再根据邻补角的概念计算，得到答案．
【详解】解：∵，
∴，
∵平分，
∴，
∴，
故选：D．
6. 估计值在（ ）
A. 3和4之间B. 4和5之间C. 5和6之间D. 6和7之间
【答案】B
【解析】
【分析】本题考查了无理数的估算，根据，即可求解．
【详解】解：∵，则，
∴，
故选：B．
7. 已知点A（1，3）与点B（x，y）在同一条平行于x轴的直线上，点B与A相距3个单位长度，则点B的坐标是（ ）
A. （1，6）B. （4，3）
C. （1，6）或（1，0）D. （4，3）或（﹣2，3）
【答案】D
【解析】
【分析】根据点A（1，3）与点B（x，y）在同一条平行于x轴的直线上，且点B与A相距3个单位长度，可知点B的纵坐标与点A的纵坐标相等，横坐标之差的绝对值为3，从而可以求出点B的坐标．
【详解】解：∵点A（1，3）与点B（x，y）在同一条平行于x轴的直线上，且点B与A相距3个单位长度，
∴y＝3，|x﹣1|＝3．
∴y＝3，x＝4或x＝﹣2．
∴点B的坐标为（4，3）或（﹣2，3）．
故选：D．
【点睛】本题考查坐标与图形的性质，解题的关键是明确与x轴平行的直线上所有点的纵坐标相同，任意一点与y轴的距离是横坐标的绝对值．
8. 的算术平方根是（ ）
A. 2B. ±2C. D.
【答案】C
【解析】
【分析】先求得的值，再继续求所求数的算术平方根即可．
【详解】∵=2，
而2的算术平方根是，
∴的算术平方根是，
故选C．
【点睛】此题主要考查了算术平方根的定义，解题时应先明确是求哪个数的算术平方根，否则容易出现选A的错误．
9. 与点 P (a²＋2，－a²－1)在同一个象限内的点是( )
A. （2，－1）B. （－1，2）C. （－2，－1）D. （2，1）
【答案】A
【解析】
【分析】根据平方数非负数的性质求出点P的横坐标与纵坐标的正负情况，再根据各象限内点的坐标特征求出点P所在的象限，然后解答即可．
【详解】解：∵a2≥0，
∴a2+2≥2，-a2-1≤-1，
∴点P在第四象限，
（2，－1）,（－1，2）,（－2，－1）,（2，1）中只有（2，-1）在第四象限．
故选A．
【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
10. 求1＋2＋22＋23＋…＋22020的值，可令S＝1＋2＋22＋23＋…＋22020，则2S＝2＋22＋23＋24＋…＋22021，因此2S－S＝22021－1．仿照以上推理，计算出1＋2020＋20202＋20203＋…＋20202020的值为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】由题意可知S＝ 1＋2020＋20202＋20203＋…＋20202020①，可得到2020S＝2020＋20202＋20203＋…＋20202020＋20202021②，然后由②－①，就可求出S的值．
【详解】解：设S＝ 1＋2020＋20202＋20203＋…＋20202020①
则2020S＝2020＋20202＋20203＋…＋20202020＋20202021②
由②－①得：
2019S＝20202021－1
∴．
故答案为：C．
【点晴】本题主要考查探索数与式的规律，有理数的加减混合运算．
第II卷（非选择题）
二、填空题（每小题4分，共20分）
11. 如图，直线，，则__________．
【答案】##38度
【解析】
【分析】本题主要考查了平行线的性质，解题的关键是熟练掌握平行线的性质，根据两直线平行，同位角相等，即可求解．
【详解】解：∵，，
∴．
故答案为：．
12. 方程是关于x，y的二元一次方程，则________．
【答案】
【解析】
【分析】本题考查二元一次方程的定义．含有两个未知数，并且含有未知数的项的次数都是1的整式方程叫做二元一次方程．根据定义可得且，由此可解．
【详解】解：由题意知且，
，，
，
故答案为：．
13. 点 P 在第二象限，且到 x 轴的距离为 6，到 y 轴的距离为 5，则点 P 的坐标为 ________．
【答案】
【解析】
【分析】本题主要考查点的坐标，熟练掌握平面直角坐标系中点的坐标特征是解题的关键；因此此题可根据题意直接写出点P的坐标．
【详解】解：由题意得：点 P 的坐标为；
故答案为．
14. 若是关于x，y的二元一次方程组的解，则的值为_____．
【答案】3
【解析】
【分析】本题主要考查了二元一次方程组的解的定义，解二元一次方程组，先把代入原方程组得到，再用即可得到答案．
【详解】解：是关于x，y的二元一次方程组的解，
∴，
得，
故答案为：3．
15. 如图，在长方形网格中，每个小长方形的长为，宽为，,两点在网格格点上，若点也在网格格点上，以,,为顶点的三角形的面积为，则满足条件的点有______个．
【答案】4
【解析】
【分析】尝试在网格中寻找符合条件的点，总共有16个点，可以依次尝试一遍．
【详解】根据题意，遍历网络中的所有点，发现符合条件的点C点如下图：
故答案为：4．
【点睛】本题考查在格点中找寻符合要求的点，此类题型，我们需要大胆尝试．
三、解答题（16-19每题6分，20-22题每题8分，23题10分，24题12分，共70）
16. ．
【答案】+．
【解析】
【分析】根据绝对值的性质化简，再根据二次根式的加减法法则合并同类二次根式.
【详解】解：原式＝﹣+2
＝+．
【点睛】本题主要考查二次根式的运算和绝对值的化简，解决本题的关键是要熟练掌握二次根式的运算法则和绝对值的性质.
17. 解方程：
【答案】
【解析】
【分析】该题主要考查了解一元二次方程-直接开平方法，熟练掌握解方程的方法是解题的关键．
由原方程得到，利用直接开平方法，方程两边直接开平方即可．
【详解】解：由原方程，得，
直接开平方，得，
解得．
18. 解方程组
【答案】
【解析】
【分析】本题考查了二元一次方程组的解法，其基本思路是消元，消元的方法有：加减消元法和代入消元法两种，灵活选择合适的方法是解答本题的关键．用加减消元法求解即可．
【详解】解：，
，得
，
∴，
把代入①，得
，
∴．
∴．
19. 解方程组：．
【答案】
【解析】
【分析】整理方程组为一般式，再利用代入消元法求解可得．
【详解】
由①得x+1=6y③
将③代入②得：2×6y﹣y=22
解得：y=2
把y=2代入③得：x+1=12
解得：x=11
∴．
【点睛】本题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
20. △ABC与在平面直角坐标系中的位置如图．
（1）分别写出下列各点的坐标： ； ； ；
（2）说明由△ABC经过怎样平移得到？
（3）求△ABC的面积．
【答案】（1）（﹣3，1），（﹣2，﹣2），（﹣1，﹣1）
（2）先向左平移4个单位，再向下平移2个单位
（3）2
【解析】
【分析】（1）根据图示即可得出、、三点的坐标；
（2）利用对应点位置变化得出答案；
（3）直接利用△ABC所在直角梯形面积减去周围三角形面积进而得出答案．
【小问1详解】
根据图示，得A′（﹣3，1），B′（﹣2，﹣2），C′（﹣1，﹣1）；
故答案为：（﹣3，1），（﹣2，﹣2），（﹣1，﹣1）．
【小问2详解】
△ABC先向左平移4个单位，再向下平移2个单位；（或先向下平移2个单位，再向左平移4个单位）得到△A′B′C′；
【小问3详解】
如图，=×(1+3)×2﹣×1×3﹣×1×1
＝2．
【点睛】本题考查了利用平移变换作图，图形与坐标，根据网络图中对应点的位置确定出平移的方法是解题的关键．
21. 若方程组和方程组有相同的解，求a，b的值．
【答案】
【解析】
【分析】解方程组得出x，y的值，将其代入方程组即可求出a与b的值．
【详解】解：将和组成方程组得，，
解得，，
将分别代入和得，，
解得．
【点睛】此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．
22. 如图， ，， ．求证：．
【答案】见解析
【解析】
【分析】本题考查平行线的性质和判定．熟练掌握平行线的性质和判定定理，并能正确识别同位角、同旁内角、内错角是解题关键．先根据已给的角度判断，从而可得，再根据等量代换可得，从而可证．
【详解】证明：∵，，
∴，
∴，
∴，
∵，
∴，
∴．
23. 如图，，
（1）在图1中，写出的数量关系，并说明理由；
（2）在图2中，（1）结论是否成立？若成立，请证明，若不成立，请你探究的数量关系，并写出你探究的结论．
【答案】（1），理由见解析；
（2）不成立，，理由见解析．
【解析】
【分析】本题考查了平行线的性质，掌握平行线的性质是解题的关键．
（1）过点作，利用平行线的性质即可得出；
（2）过点作，利用平行线的性质即可得出．
【小问1详解】
解：如图：过点作，
∵，
∴，
∴，
，
∴，
∵，
∴．
【小问2详解】
解：不成立，理由如下：
如图：过点作，
∵，
∴，
∴，，
∴，
∵，
∴．
24. 在平面直角坐标系中，已知点，，，且满足，线段交轴于点，点是轴正半轴上的一点．
（1）求出点，的坐标；
（2）如图2，若，，分别平分，；求（用含的代数式表示）；
（3）如图3，坐标轴上是否存在一点，使得的面积和的面积相等？若存在请求出点坐标；若不存在，请说明理由．
【答案】（1），
（2）
（3）存在， 或或或
【解析】
【分析】（1）根据非负数的性质得，，解方程即可得出和的值，从而得出答案；
（2）过点作，交轴于点，根据角平分线的定义得，，再利用平行线的性质可得答案；
（3）连接，利用两种方法表示的面积，可得点的坐标，再分点在轴或轴上两种情形，分别表示的面积，从而解决问题．
【小问1详解】
解：∵，
∴，，
∴，，
∴、；
【小问2详解】
解：如图，过点作，

∴，
又∵，
∴，
∴，
∵，，
∴，
又∵，分别平分，，，
∴，，
∴，，
∴；
【小问3详解】
解：连接，如图．

设，
∵，
∴，
解得，
∴点坐标为，，
当点在轴上时，设，
∵，
∴，
解得或，
∴此时点坐标为或，
当点在轴上时，设，
，
解得或，
∴此时点坐标或，
综上可知存在满足条件的点，其坐标为或或或．
【点睛】本题是三角形综合题，主要考查了非负数的性质，角平分线的定义，角的和差关系，三角形的面积等知识，利用分割法表示三角形的面积是解题的关键．