



黑龙江省大庆市实验中学实验二部2023-2024学年高一下学期期中考试数学试卷(原卷版+解析版)
展开1. 定义运算,则满足(为虚数单位)的复数在复平面内对应的点在( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
【答案】A
【解析】
【分析】先根据定义结合复数的乘法运算求出复数,再根据复数的几何意义即可得解.
【详解】由题意可得,
即,
所以复数在复平面内对应的点为,在第一象限.
故选:A.
2. 下列命题中正确的是( )
①圆锥的轴截面是所有过顶点的截面中面积最大的一个;
②在圆柱的上、下底面的圆周上各取一个点,则这两点的连线是圆柱的母线;
③圆台的两个底面平行.
A ①②B. ②C. ③D. ①③
【答案】C
【解析】
【分析】对①,根据过圆锥顶点的截面图形特征和截面图的面积公式即可判断;对②③,依次根据圆柱的母线定义和圆台定义即可判断.
【详解】对①,过圆锥顶点的截面为等腰三角形,且两腰长为母线长,
设该等腰三角形顶角为,则截面三角形面积为,显然当,面积最大,
故当圆锥的轴截面三角形顶角大于时,圆锥的轴截面面积不一定是最大的,故①错;
根据圆柱的母线定义可知②错;
根据圆台定义:平行于圆锥底面的平面去截圆锥,截面与圆锥底面的部分称为圆台,知圆台的两个底面平行,故③正确.
故选:C.
3. P为四边形ABCD所在平面上一点,,则P为( ).
A. 四边形ABCD对角线交点B. AC中点
C. BD中点D. CD边上一点
【答案】B
【解析】
【分析】先由三角形法则得到,结合题目条件得到即可求解.
【详解】,,即,
故,,故P为AC中点.
故选:B.
4. 已知,且的夹角为,则在方向上的投影向量为( )
A. B. C. D.
【答案】B
【解析】
【分析】根据题意先求出数量积,再根据投影向量公式需求求出,进而根据投影向量公式即可求解.
【详解】由题,
所以,
所以在方向上的投影向量为.
故选:B.
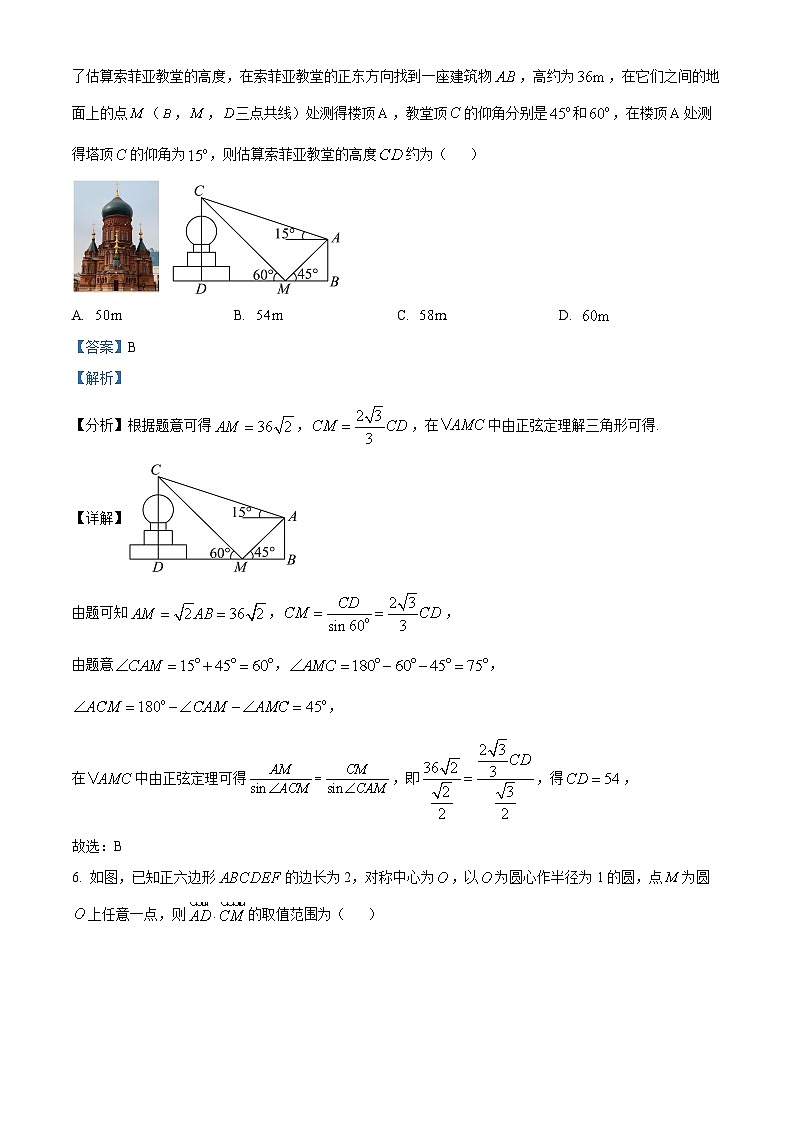
5. 圣•索菲亚教堂是哈尔滨的标志性建筑,其中央主体建筑集球、圆柱、棱柱于一体,极具对称之美.为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物,高约为,在它们之间的地面上的点(,,三点共线)处测得楼顶,教堂顶的仰角分别是和,在楼顶处测得塔顶的仰角为,则估算索菲亚教堂的高度约为( )
A. B. C. D.
【答案】B
【解析】
【分析】根据题意可得,,在中由正弦定理解三角形可得.
【详解】
由题可知,,
由题意,,,
在中由正弦定理可得,即,得,
故选:B
6. 如图,已知正六边形的边长为2,对称中心为,以为圆心作半径为1的圆,点为圆上任意一点,则的取值范围为( )
A. B. C. D.
【答案】C
【解析】
【分析】解法一 连接,,设,根据向量的线性运算用,表示出,然后结合三角函数的性质即可求得结果.
解法二 以为坐标原点建立平面直角坐标系,设,根据数量积的坐标表示得到,再结合三角函数的性质即可求得结果.
解法三 借助向量投影的知识将转化,找到取得最值时点的位置,即可求得结果.
【详解】解法一 :如图所示:
连接,设,连接,依题意得,,,,
则,
.
因为,所以,(三角函数的有界性)
所以.
故选:C.
解法二 如图,
以为坐标原点,以直线为轴,过且和垂直的直线为轴建立平面直角坐标系,
则依题意可得,,,
因为圆的半径为1,所以可设,
所以,,所以,
又,(三角函数有界性)
所以.
故选:C.
解法三 如图所示:
设,则.
可看成是在上的投影,
当点与重合时最小,最小值为,
当点与重合时最大,最大值为0,
故.
故选:C.
7. 在中,角的对边分别为,若,又的面积,且,则( )
A. 64B. 84C. -69D. -89
【答案】C
【解析】
【分析】利用正弦定理边化角,结合两角和差正弦公式整理可求得关系,再由三角形面积公式和余弦定理求得三边,再由数量积运算得到结果
【详解】解法一:由,得,
则,
即,即,
又,即;
又,得;
综上.
则,即.
由,
平方知
所以.
解法二:
.
故选:.
8. 在中,角A,B,C的对边分别为a,b,c,S为的面积,,且,则的周长的取值范围是( )
A. B. C. D.
【答案】B
【解析】
【分析】利用余弦定理结合三角形面积公式求出,利用正弦定理表示,求出周长最大值,进而利用三角形的性质求解即可.
【详解】若,则由余弦定理得,
而由面积公式得,故,
则,则,则,
则有,而在中,可得,
由二倍角公式得,故,,
由正弦定理得,则,
可得,
,而,则,
显然当时,最大,且此时,故,
而易知,综上,
故选:B
【点睛】关键点点睛:本题考查求解三角形,解题关键是求出,然后表示出,由三角函数和三角形性质得到所要求的取值范围即可.
二、多项选择题(本大题共4小题,每小题5分,共20分)
9. 设复数在复平面内对应的点为,原点为,为虚数单位,则下列说法正确的是( )
A. 若,则或
B. 若点的坐标为,则对应的点在第三象限
C. 若,则模为
D. 若,则点的集合所构成的图形的面积为
【答案】BD
【解析】
【分析】由复数的模判断AC;由复数的基本概念和几何意义判断BD.
【详解】对A,由,可得,且,故A错误;
对B,若点的坐标为,则故对应的点的坐标为,在第三象限,故B正确;
对C,若,则的模为,故C错误;
对D,设,若,则,
则点的集合所构成的图形的面积为,故D正确.
故选:BD.
10. 下列说法中正确的是( )
A. 在中,,则的面积为
B. 已知向量,则
C. 在中,若,则是等腰三角形
D. 已知向量与的夹角为钝角,则的取值范围是
【答案】AC
【解析】
【分析】由三角形面积公式直接求解可判断A;根据向量坐标运算求解可判断B;记的中点为D,根据向量加法运算结合已知可得中线垂直于,然后可判断C;考虑与反向时不满足条件即可判断D.
【详解】,故A正确;
,故B错误;
记的中点为D,由于,
因此中线垂直于,所以是等腰三角形,故C正确;
与的夹角为钝角,
且,故D错误.
故选:AC.
11. 在中,,则下列结论正确的是( )
A. 若,则有两解B. 面积有最大值
C. 若是钝角三角形,则BC边上的高AD的范围为D. 周长最大值为6
【答案】ABC
【解析】
【分析】对于A,根据判断即可;对于BCD,均可先由正弦定理边化角得,,再依次由、、结合三角恒等变换公式以及三角函数值的范围即可研究面积、高和周长的取值范围.
【详解】对于A,由正弦定理得,所以,
故有两解,故A正确;
对于B,由题及正弦定理得,,
所以
,
又,所以,所以,
所以,
所以,
所以面积最大值为.故B正确;
对于C,因为,
所以对于BC边上的高AD,角或角为钝角的情况是等价的,不妨令角C为钝角,
因为,
所以由选项B有,
则由得,所以,
所以,所以,
所以若是钝角三角形,则BC边上的高AD的范围为.
对于D,由选项B得周长为
,
又,所以,所以,
所以最大值为,
即周长最大值为.故D错误;
故选:ABC.
【点睛】方法点睛:解三角形中边长、周长、面积或角度有关的最值或范围问题常用处理思路:
①余弦定理结合基本不等式构造不等式关系;
②采用正弦定理边化角,利用三角函数值的范围求出最值或范围.如果三角形有限制为锐角或钝角三角形条件或其他的限制条件,通常采用这种方法.
12. 对于非零向量,定义变换,得到一个新的向量,则关于该变换,下列说法正确的是( )
A. 若为任意实数,则B. 若,则
C. 若,则D. 存在使得
【答案】ABC
【解析】
【分析】由定义变换的新向量,结合数乘运算定义判断选项A,结合向量平行的条件验证选项B,结合向量垂直的条件验证选项C,由向量夹角的坐标运算验证选项D.
【详解】对于选项A,因为,所以,
所以,故A正确;
对于选项B,,设,若,则,
,,
所以,即,故B正确;
对于选项C,若,则,
所以,故C正确;
对于选项D,,
,所以,故D错误.
故选:ABC.
三、填空题(本大题共4小题,每小题5分,共20分)
13. 如图,矩形是水平放置的一个平面图形的直观图,其中,则原图面积为______.
【答案】
【解析】
【分析】根据直观图和原图的关系,由可求解.
【详解】解:由题可得直观图面积:,
由可得:原图面积为:,
故答案为:.
14. 已知为的边上一点,,,,则______.
【答案】##
【解析】
【分析】由已知可得,则,设,然后在中利用余弦定理可求出,再在中,利用正弦定理可求得结果
【详解】因为,所以,
所以由,得,
所以.
设,则,,
在中,由余弦定理得,
即,解得.
所以,.
在中,由正弦定理得,
故.
故答案为:
15. 在中,已知,是的外心,若,则______.
【答案】
【解析】
【分析】通过正弦定理,求出外接圆的半径,求出与的数量积,列方程求得结果.
【详解】中,已知,由余弦定理可得:
,则,
是的外心,设的外接圆半径为,
由正弦定理可得:,可得,
分别为的中点,如图所示,
,,
,,
,
又,,
解得,所以.
故答案为:.
16. 在锐角三角形中,角的对边分别为,若,则的最小值是_______.
【答案】
【解析】
【分析】由正弦定理化简边角关系式,可整理出;根据,结合两角和差正切公式可得到;利用换元的方式可将问题转变为求解的最小值的问题;根据锐角三角形特点可求出,从而利用基本不等式求解出最小值.
【详解】由正弦定理可得:
得:
,即
又
令,得:
为锐角三角形
得:,即
当且仅当,即时取等号
本题正确结果:
【点睛】本题考查正弦定理化简边角关系式、两角和差正切公式的应用、基本不等式求解和的最小值问题,关键是能够将所求式子利用两角和差正切公式进行化简,采用换元的方式可将问题转化为函数最值类问题的求解.
四、解答题(本大题共6小题,其中17题10分,18-22题各12分,共70分)
17. 已知z是复数,与均为实数.
(1)求复数z;
(2)复数在复平面上对应的点在第一象限,求实数a的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)根据复数的运算法则,结合复数的特征,即可求解;
(2)根据(1)的结果,计算复数的平方,再根据复数的几何意义,即可求解.
【小问1详解】
设,,所以,
由条件得,且,
所以,所以,
【小问2详解】
,
由条件得,
解得,所以所求实数a的取值范围是.
18. 已知a,b,c分别为三个内角A,B,C的对边,且.
(1)求;
(2)若的面积为,求的周长.
【答案】(1)
(2)10
【解析】
【分析】(1)根据给定条件,利用正弦定理边化角,再借助和角的正弦公式求解作答.
(2)由(1)的结论,利用三角形面积公式、余弦定理求出即可作答.
【小问1详解】
,由正弦定理可得,
因,
所以,可得,
为三角形内角,,解得,;
【小问2详解】
,
,
由余弦定理得,
即,解得,
的周长为.
19. 在直角梯形中,//.
(1)求;
(2)若与共线,求的值;
(3)若为边上的动点(不包括端点),求的最小值.
【答案】(1);
(2);
(3).
【解析】
【分析】(1)以为坐标原点,建立平面直角坐标系,写出各点坐标,求得的坐标,利用数量积的坐标运算即可求得结果;
(2)根据(1)中所求点的坐标,写出与的坐标,根据向量共线的坐标表示,即可求得参数值;
(3)设,求出点的坐标,再求得关于的函数关系,进而求得函数的最小值即可求得结果.
【小问1详解】
过作,易知,又,故可得;
以为坐标原点,建立平面直角坐标系,如下所示:
则,,
故.
【小问2详解】
由(1)可知,,
故,
若与共线,则,解得.
【小问3详解】
设,则,易知,
则
则,
对,其对称轴,故其最小只能为;
故的最小值为.
20. 如图:在中,已知与交于点.
(1)用向量表示向量;
(2)过点作直线,分别交线段于点,设,若,,当取得最小值时,求模长.
【答案】(1)
(2)5
【解析】
【分析】(1)设,将向量分别用和表示,根据三点共线可求值;;
(2)将向量用表示,由三点共线,可得,由基本不等式可解.
【小问1详解】
设,将代入,
得,因为三点共线,且三点共线,
所以,得
即.
【小问2详解】
,
则,因为三点共线,
则,即
当且仅当,即时取得等号.
此时
.
21. 如图,半圆的直径为为直径延长线上的点,为半圆上任意一点,以AB为一边作等边三角形ABC.设.
(1)当时,求四边形OACB的周长;
(2)著作《天文集》中涉及如下定理:任意凸四边形中,两条对角线的乘积小于或等于两组对边乘积之和,当且仅当对角互补时取等号,根据以上材料,则当线段OC的长取最大值时,求.
(3)求四边形OACB的面积最大值.
【答案】(1)
(2)
(3)
【解析】
【分析】(1)结合已知利用余弦定理可求,即可得到所求四边形的周长;
(2)由已知条件分析出的最大值并得到,之间的关系,由此借助余弦定理求解出的长度,再利用余弦定理即可求解出的大小;
(3)先由余弦定理求,再由三角形的面积公式和等边三角形的面积公式,结合辅助角公式和正弦函数的最值,可得所求结论.
【小问1详解】
在中,由余弦定理得,
即,于是四边形OACB的周长为;
【小问2详解】
因,且为等边三角形,,,
所以,所以,
即OC的最大值为3,取等号时,
所以,
不妨设,
则,解得,
所以,
所以;
【小问3详解】
在中,由余弦定理得,
所以,,
于是四边形OACB的面积为
,
当,即时,四边形OACB的面积取得最大值为,
所以,当B满足时,四边形OACB的面积最大,最大值为.
22. 在中,角所对的边分别是,且满足.
(1)求角;
(2)求的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)利用正弦定理进行边角互化,结合辅助角公式进行求解;
(2)对待求表达式使用正弦定理边角互化,得到,然后消去一个变量,使得原式是关于的三角函数表达式,结合二倍角公式,二次函数的知识点求解.
【小问1详解】
,由正弦定理得,
,
因为,
所以,
即,
因为,所以,故,
所以,
因为,所以,
故,解得;
【小问2详解】
由(1)知,根据正弦定理,
则
,
令,
因为,所以,,
则,
故当时,取得最小值,最小值为,
当时,取得最大值,最大值为,
故的取值范围是.
黑龙江省大庆市实验中学实验二部2023-2024学年高二下学期期中考试数学试卷(Word版附解析): 这是一份黑龙江省大庆市实验中学实验二部2023-2024学年高二下学期期中考试数学试卷(Word版附解析),共11页。试卷主要包含了单选题,多选题,填空题等内容,欢迎下载使用。
黑龙江省大庆市实验中学实验二部2023-2024学年高三下学期得分训练(三)数学试卷: 这是一份黑龙江省大庆市实验中学实验二部2023-2024学年高三下学期得分训练(三)数学试卷,共6页。
江苏省南菁高级中学实验班2023-2024学年高一下学期期中考试数学试卷(原卷版+解析版): 这是一份江苏省南菁高级中学实验班2023-2024学年高一下学期期中考试数学试卷(原卷版+解析版),文件包含江苏省南菁高级中学实验班2023-2024学年高一下学期期中考试数学试卷原卷版docx、江苏省南菁高级中学实验班2023-2024学年高一下学期期中考试数学试卷解析版docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。












