2024北京高考冲刺数学大刷题之常考几何与代数部分（二）

这是一份2024北京高考冲刺数学大刷题之常考几何与代数部分（二），共17页。试卷主要包含了3），  =，且  ，则m=，那么该几何体的体积为等内容，欢迎下载使用。

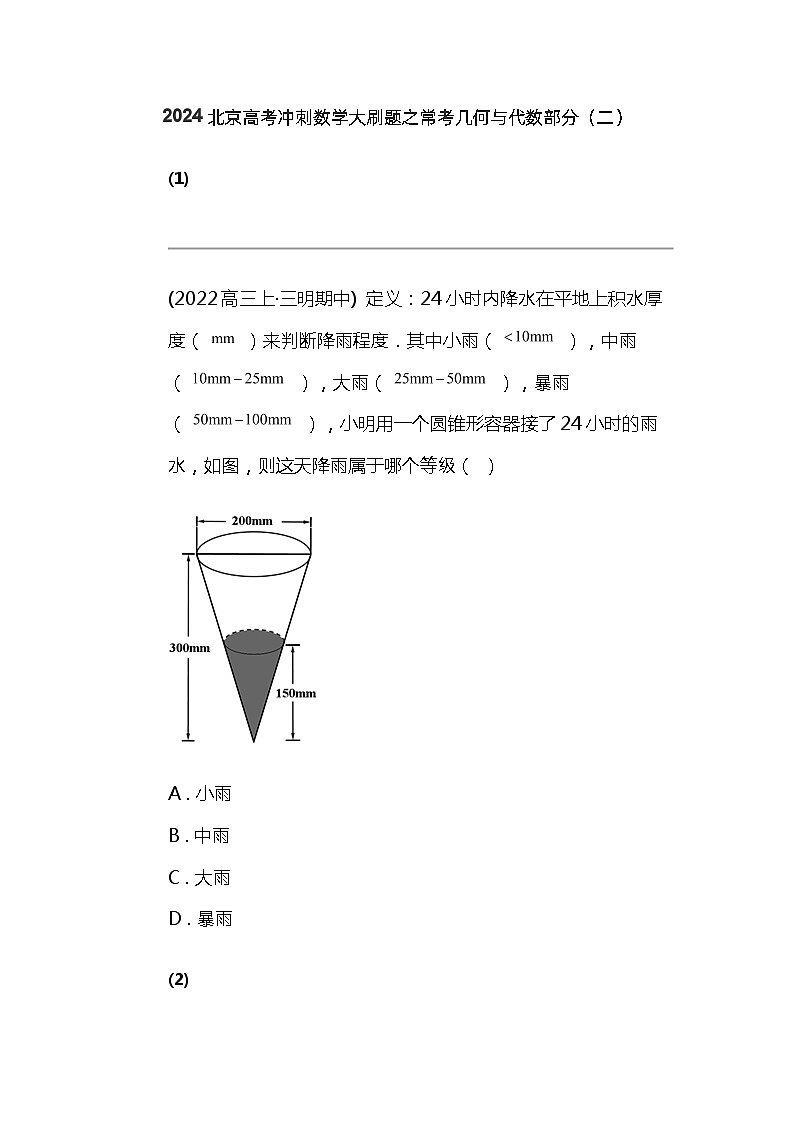
(2022高三上·三明期中) 定义：24小时内降水在平地上积水厚度（ ）来判断降雨程度．其中小雨（ ），中雨（ ），大雨（ ），暴雨（ ），小明用一个圆锥形容器接了24小时的雨水，如图，则这天降雨属于哪个等级（ ）
A . 小雨
B . 中雨
C . 大雨
D . 暴雨
(2)
， ， ，则 ； ．
(3)
已知抛物线 ，焦点为 ，点 为抛物线 上的点，且 ，则 的横坐标是；作 轴于 ，则 ．
(4)
(2024九下·南宁月考) 已知在 中， ， ．
（1） 求 的大小；
（2） 在下列三个条件中选择一个作为已知，使 存在且唯一确定，并求出 边上的中线的长度．
① ；②周长为 ；③面积为 ；
(5)
(2021高二下·娄星期中) 如图，在四棱锥 中，底面 为菱形， ， ， 为线段 的中点， 为线段 上的一点.
（1） 证明：平面 平面 .
（2） 若 ，二面角 的余弦值为 ，求 与平面 所成角的正弦值.
(6)
(2021高一下·大荔期末) 已知向量 ，若 ，则 （ ）
A . -4
B .
C .
D . 4
(7)
(2024·阳江模拟) 已知椭圆C： ，过点 的直线l交椭圆C于点A ， B.
（1） 当直线l与x轴垂直时，求 ；
（2） 在x轴上是否存在定点P ， 使 为定值？若存在，求点P的坐标及 的值；若不存在，说明理由.
(8)
(2021·富平模拟) 已知双曲线 的渐近线与圆 相切，则 （ ）
A . 3
B .
C .
D .
(9)
(2020高三上·玉溪期中) 如图，半椭圆 与半椭圆 组成的曲线称为“果圆”，其中 . 和 分别是“果圆”与x轴，y轴的交点.给出下列三个结论：
① ；②若 ，则 ；③若在“果圆”y轴右侧部分上存在点P ， 使用 ，则 .
其中，所有正确结论的序号是（ ）
A . ①②
B . ①③
C . ②③
D . ①②③
(10)
已知棱长为1的正方体 ， 是 的中点，动点 在正方体内部或表面上，且 平面 ，则动点 的轨迹所形成区域的面积是（ ）
A .
B .
C . 1
D . 2
(11)
(2022高二上·大同期中) 如图，在正方体 中，E为 的中点．
（1） 求证： 平面 ；
（2） 求直线 与平面 所成角的正弦值．
(12)
(2021高一下·东莞期中) 在 中， ，点P是 的中点，则 （ ）
A .
B . 4
C .
D . 6
(13)
(2021高二下·梅州期末) 已知复数z满足 ，则z的虚部是（ ）
A . -1
B . 1
C .
D . i
(14)
(2021高二下·番禺期末) 如图，在长方体 中，四边形 是边长为1的正方形， ，M ， N分别为 的中点.
（1） 求证： 平面 ；
（2） 求直线 与平面 所成角的正弦值.
(15)
(2023高一上·温州期中) 某四棱锥的三视图如图所示，该四棱锥的体积为（ ）
A .
B . 9
C .
D . 27
(16)
(2021高二下·番禺期末) 已知圆 截直线 所得弦的长度为1，那么k的值为（ ）
A .
B .
C . 1
D .
(17)
(2022高三上·西城期末) 在复平面内，复数 对应的点位于（ ）
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
(18)
(2021高一下·安吉期末) 如图，在四棱锥 中，O是 边的中点， 底面 ．在底面 中， ．
（1） 求证： 平面 ；
（2） 求二面角 的余弦值．
(19)
(2020高二上·上海月考) 设抛物线的顶点为O，焦点为F，准线为l．P是抛物线上异于O的一点，过P作 于Q，则线段 的垂直平分线（ ）．
A . 经过点O
B . 经过点P
C . 平行于直线
D . 垂直于直线
(20)
(2022九上·秦安期末) 在 中， ，再从条件①、条件②这两个条件中选择一个作为已知，求：
（Ⅰ）a的值：
（Ⅱ） 和 的面积．
条件①： ；
条件②： ．
注：如果选择条件①和条件②分别解答，按第一个解答计分．
(21)
(2023高二上·潮州期末) 如图，在正方体 中，E为 的中点．
（Ⅰ）求证： 平面 ；
（Ⅱ）求直线 与平面 所成角的正弦值．
(22)
(2023九上·福田期中) 已知正方形 的边长为2，点P满足 ，则 ； ．
(23)
在复平面内，复数z对应的点的坐标是 ，则 （ ）．
A .
B .
C .
D .
(24)
某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为（ ）．
A .
B .
C .
D .
(25)
(2023高三上·西城期末) 设抛物线y2=4x的焦点为F，准线为l.则以F为圆心，且与l相切的圆的方程为.
(26)
已知双曲线 （a>0）的离心率是 ，则a=（ ）
A .
B . 4
C . 2
D .
(27)
已知向量 =（-4.3）， =（6，m），且 ，则m=.
(28)
在△ABC中，a=3，b-c=2，csB=- .
（I）求b，c的值：
（II）求sin（B+C）的值.
(29)
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为菱形，E为CD的中点.
（Ⅰ）求证：BD⊥平面PAC；
（Ⅱ）若∠ABC=60°，求证：平面PAB⊥平面PAE；
（Ⅲ）棱PB上是否存在点F，使得CF∥平面PAE？说明理由.
(30)
(2020高三上·北京月考) 某几何体是由一个正方体去掉一个四棱柱所得.其三视图如图所示.如果网格纸上小正方形的边长为1.那么该几何体的体积为.