

2023-2024学年陕西省西安市碑林区西北工大附中七年级(下)期中数学试卷(含解析)
展开
这是一份2023-2024学年陕西省西安市碑林区西北工大附中七年级(下)期中数学试卷(含解析),共21页。试卷主要包含了选择题,解答题等内容,欢迎下载使用。
1.(3分)下列计算正确的是( )
A.a3•a3=a9B.(a3)3=a6C.a6÷a3=a2D.a3+a3=2a3
2.(3分)下列图案中,是轴对称图形的是( )
A.B.C.D.
3.(3分)科学家在实验室中检测出某种病毒的直径约为0.000103毫米,该直径用科学记数法表示为( )毫米.
A.0.103×10﹣3B.1.03×10﹣4
C.0.103×10﹣4D.10.3×10﹣5
4.(3分)如图,已知AB∥CD,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10°B.20°C.30°D.40°
5.(3分)若a﹣b=8,a2﹣b2=72,则a+b的值为( )
A.9B.﹣9C.27D.﹣27
6.(3分)具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠CB.∠A+∠B=90°
C.∠A:∠B:∠C=1:2:3D.∠A=∠B=3∠C
7.(3分)已知两个变量x和y,它们之间的3组对应值如表:则y与x之间的表达式可能是( )
A.y=xB.y=2x+1C.y=x﹣1D.
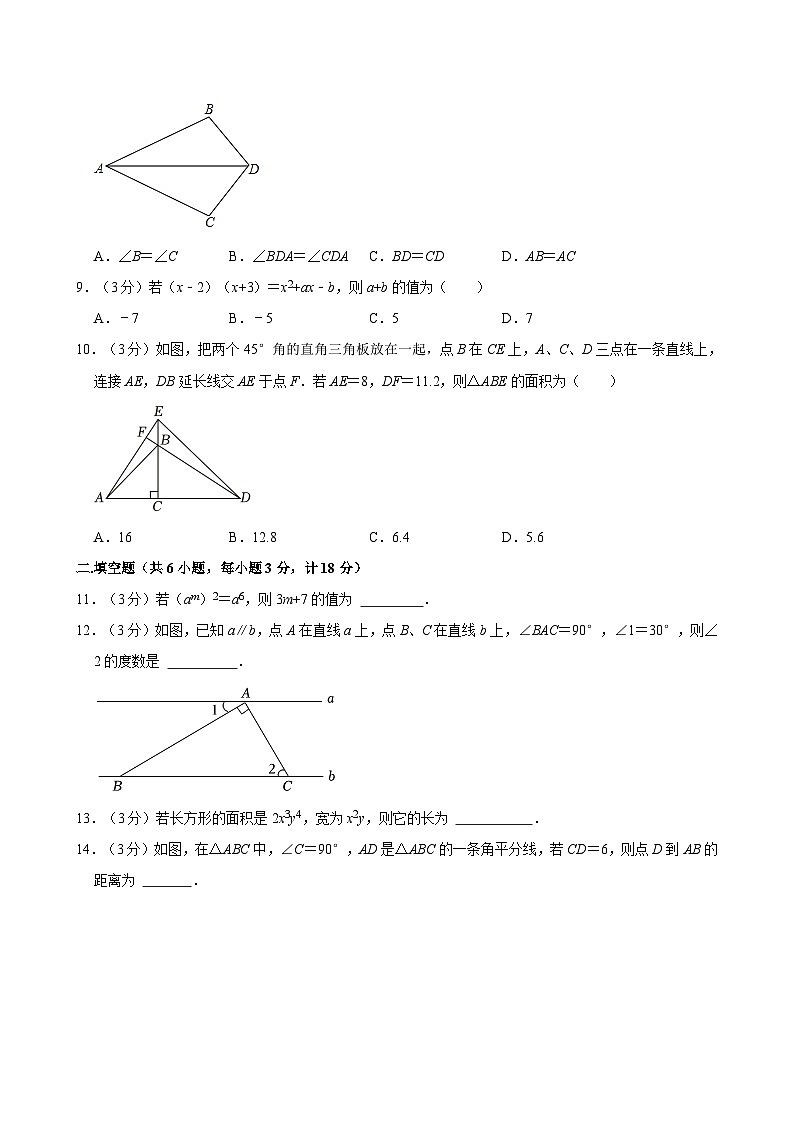
8.(3分)如图,AD为∠BAC的平分线,添加下列条件后,不能证明△ABD≌△ACD的是( )
A.∠B=∠CB.∠BDA=∠CDAC.BD=CDD.AB=AC
9.(3分)若(x﹣2)(x+3)=x2+ax﹣b,则a+b的值为( )
A.﹣7B.﹣5C.5D.7
10.(3分)如图,把两个45°角的直角三角板放在一起,点B在CE上,A、C、D三点在一条直线上,连接AE,DB延长线交AE于点F.若AE=8,DF=11.2,则△ABE的面积为( )
A.16B.12.8C.6.4D.5.6
二.填空题(共6小题,每小题3分,计18分)
11.(3分)若(am)2=a6,则3m+7的值为 .
12.(3分)如图,已知a∥b,点A在直线a上,点B、C在直线b上,∠BAC=90°,∠1=30°,则∠2的度数是 .
13.(3分)若长方形的面积是2x3y4,宽为x2y,则它的长为 .
14.(3分)如图,在△ABC中,∠C=90°,AD是△ABC的一条角平分线,若CD=6,则点D到AB的距离为 .
15.(3分)已知a、b为等腰△ABC的边长,且满足|a﹣5|+(b﹣11)2=0,则△ABC的底边长是 .
16.(3分)如图,在△ABC中,BC=8,S△ABC=40,点P是BC边上一动点,连接AP,在AP的上方作等边三角形APQ,则△APQ周长的最小值为 .
三、解答题(共7道题,计52分,解答要写出过程)
17.(8分)(1);
(2)(3a2b)2÷(﹣3a3b)•(﹣2ab3).
18.(5分)如图,在△ABC中,AB=AC,AD是BC边上的高.请用尺规作图法,在AD上求作一点P使得PA=PB=PC.(保留作图痕迹,不写作法)
19.(6分)先化简,再求值:(2a﹣1)2+6a(a+1)﹣(3a﹣2)(3a+2),其中a2+2a﹣2024=0.
20.(7分)已知:如图,AB∥DE,AB=DE,AF=DC.求证:∠B=∠E.
21.(8分)小明在学习完乘法公式后,发现完全平方公式经过适当的变形或数形结合,可以解决很多数学问题.
例如:若a+b=5,ab=6,求a2+b2的值.
解:∵a+b=5,ab=6,
∴(a+b)2=25,2ab=12,
∴a2+b2+2ab=25.
∴a2+b2=13.
(1)若m﹣n=3,mn=54,求m2+n2的值.
(2)请同学们根据上面的解题思路与方法,结合几何图形解决下列问题:如图,C是线段AB上的一点,分别以AC,BC为边向两边作正方形ACDE和正方形BCFG,设AB=10,两个正方形的面积和为52,求△FCA的面积.
22.(8分)小玲和弟弟小亮分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步中途改为步行,到达图书馆恰好用30min.小亮骑自行车以300m/min的速度直接回家,两人离家的路程y(m)与各自离开出发地的时间x(min)之间的图象关系如图所示.
(1)家与图书馆之间的路程为 m,小玲步行的速度为 m/min;
(2)求小玲和弟弟小亮途中相遇的时间.
23.(10分)发现问题
(1)已知,如图①,在四边形ABCD中,E在BC上,AE=DE,∠ABE=∠AED=∠ECD,若AB=5,BC=12,则BE= .
探究问题
(2)如图②,已知长方形ABCD的周长为36,CD=10,点E为AD边上一点,EG⊥EF分别交AB于点G,交CD于点F,且EG=EF,求四边形BCFG的面积.
解决问题
(3)如图③,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB=13,以AB为边在其左上方作正方形ABEF,FD垂直于CA延长线于点D,连接AE,M、N分别为AE、BC上两动点,连接FM,BM,MN,当BM+MN的值最小时,求多边形EFMNB的面积.(注:四边相等,四个角是直角的四边形是正方形,正方形是轴对称图形,对角线是其一条对称轴)
2023-2024学年陕西省西安市碑林区西北工大附中七年级(下)期中数学试卷
参考答案与试题解析
一、选择题(共10小题,每题3分,计30分,每小题只有一个选项是符合题意的)
1.(3分)下列计算正确的是( )
A.a3•a3=a9B.(a3)3=a6C.a6÷a3=a2D.a3+a3=2a3
【分析】利用同底数幂的乘法法则,幂的乘方的法则,同底数幂的除法法则,合并同类项法则对每个选项进行分析,即可得出答案.
【解答】解:∵a3•a3=a6≠a9,
∴选项A不符合题意;
∵(a3)3=a9≠a6,
∴选项B不符合题意;
∵a6÷a3=a3≠a2,
∴选项C不符合题意;
∵a3+a3=2a3,
∴选项D符合题意;
故选:D.
【点评】本题考查了同底数幂的乘法,幂的乘方,同底数幂的除法,合并同类项,掌握同底数幂的乘法法则,幂的乘方的法则,同底数幂的除法法则,合并同类项法则是解决问题的关键.
2.(3分)下列图案中,是轴对称图形的是( )
A.B.C.D.
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】解:A,B、D选项中的图形都不能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
C选项中的图形能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:C.
【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
3.(3分)科学家在实验室中检测出某种病毒的直径约为0.000103毫米,该直径用科学记数法表示为( )毫米.
A.0.103×10﹣3B.1.03×10﹣4
C.0.103×10﹣4D.10.3×10﹣5
【分析】用科学记数法表示较小的数,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂.
【解答】解:0.000103=1.03×10﹣4.
故选:B.
【点评】本题主要考查了用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
4.(3分)如图,已知AB∥CD,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10°B.20°C.30°D.40°
【分析】由∠AEC为△CED的外角,利用外角性质求出∠D的度数,再利用两直线平行内错角相等即可求出∠A的度数.
【解答】解:∵∠AEC为△CED的外角,且∠C=20°,∠AEC=50°,
∴∠AEC=∠C+∠D,即50°=20°+∠D,
∴∠D=30°,
∵AB∥CD,
∴∠A=∠D=30°.
故选:C.
【点评】此题考查了平行线的性质,以及外角性质,熟练掌握平行线的性质是解本题的关键.
5.(3分)若a﹣b=8,a2﹣b2=72,则a+b的值为( )
A.9B.﹣9C.27D.﹣27
【分析】第二个等式左边利用平方差公式分解,将第一个等式代入计算即可求出a+b的值.
【解答】解:∵a﹣b=8,a2﹣b2=(a+b)(a﹣b)=72,
∴a+b=9,
故选:A.
【点评】此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.
6.(3分)具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠CB.∠A+∠B=90°
C.∠A:∠B:∠C=1:2:3D.∠A=∠B=3∠C
【分析】根据三角形内角和为180度,求出每一个角的度数即可得到答案.
【解答】解:A、∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,即∠C=90°,
∴△ABC是直角三角形,不符合题意;
B、∵∠A+∠B=90°,∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,不符合题意;
C、∵∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,
∴,
∴△ABC是直角三角形,不符合题意;
D、∵∠A=∠B=3∠C,∠A+∠B+∠C=180°,
∴,即,
∴△ABC不是直角三角形,符合题意;
故选:D.
【点评】本题主要考查了三角形内角和定理,熟知三角形三个内角的度数之和为180度是解题的关键.
7.(3分)已知两个变量x和y,它们之间的3组对应值如表:则y与x之间的表达式可能是( )
A.y=xB.y=2x+1C.y=x﹣1D.
【分析】由表格可知,x每增加1,对应的y增加2,根据“y值的增加量=2×x的增加量”写出y与x之间的表达式即可.
【解答】解:由表格可知,x每增加1,对应的y增加2,
由此得y﹣1=2(x﹣0),
经整理,得y=2x+1.
故选:B.
【点评】本题考查函数关系式,找到变量变化的规律是解题的关键.
8.(3分)如图,AD为∠BAC的平分线,添加下列条件后,不能证明△ABD≌△ACD的是( )
A.∠B=∠CB.∠BDA=∠CDAC.BD=CDD.AB=AC
【分析】根据“AAS”对A进行判断;根据“ASA”对B进行判断;根据“SSA”对C进行判断;根据“SAS”对D进行判断.
【解答】解:A、由,可得到△ABD≌△ACD,所以A选项不正确;
B、由,可得到△ABD≌△ACD,所以B选项不正确;
C、由BD=CD,AD=AD,∠BAD=∠CAD,不能得到△ABD≌△ACD,所以C选项正确.
D、由,可得到△ABD≌△ACD,所以D选项不正确;
故选:C.
【点评】本题考查了全等三角形的判定:判定三角形全等的方法有“SSS”、“AAS”、“SAS”、“ASA”.
9.(3分)若(x﹣2)(x+3)=x2+ax﹣b,则a+b的值为( )
A.﹣7B.﹣5C.5D.7
【分析】先根据多项式乘多项式法则展开,合并同类项,求出a、b值,再代入求出即可.
【解答】解:(x﹣2)(x+3)
=x2+3x﹣2x﹣6
=x2+x﹣6,
∵(x﹣2)(x+3)=x2+ax﹣b,
∴a=1,b=6,
∴a+b=1+6=7,
故选:D.
【点评】本题考查了多项式乘多项式法则,能正确根据多项式乘多项式法则展开是解此题的关键.
10.(3分)如图,把两个45°角的直角三角板放在一起,点B在CE上,A、C、D三点在一条直线上,连接AE,DB延长线交AE于点F.若AE=8,DF=11.2,则△ABE的面积为( )
A.16B.12.8C.6.4D.5.6
【分析】由△ABC和△DEC都是等腰直角三角形,∠ACB=∠DCE=90°,得AC=BC,EC=DC,可根据“SAS”证明△ACE≌△BCD,得∠AEC=∠BDC,AE=BD=8,则∠DFE=∠EAC+∠BDC=∠EAC+∠AEC=90°,再求得BF=DF﹣BD=3.2,则S△ABE=AE•BF=12.8,于是得到问题的答案.
【解答】解:∵△ABC和△DEC都是等腰直角三角形,∠ACB=∠DCE=90°,
∴AC=BC,EC=DC,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠AEC=∠BDC,AE=BD=8,
∴∠DFE=∠EAC+∠BDC=∠EAC+∠AEC=90°,
∴BF⊥AE,
∵DF=11.2,
∴BF=DF﹣BD=11.2﹣8=3.2,
∴S△ABE=AE•BF=×8×3.2=12.8,
故选:B.
【点评】此题重点考查全等三角形的判定与性质、直角三角形的两个锐角互余、三角形的一个外角等于与它不相邻的两个内角的和、三角形的面积公式等知识,证明△ACE≌△BCD是解题的关键.
二.填空题(共6小题,每小题3分,计18分)
11.(3分)若(am)2=a6,则3m+7的值为 16 .
【分析】根据幂的乘方,底数不变,指数相乘即可求出m的值,然后代入代数式3m+7中求值即可.
【解答】解:∵(am)2=a6,
∴a2m=a6,
∴2m=6,
解得m=3,
∴3m+7=3×3+7=16,
故答案为:16.
【点评】本题考查了幂的乘方,代数式求值,熟练掌握幂的乘方的运算法则是解题的关键.
12.(3分)如图,已知a∥b,点A在直线a上,点B、C在直线b上,∠BAC=90°,∠1=30°,则∠2的度数是 60° .
【分析】根据平行线的性质与三角形的内角和为180°进行解题即可.
【解答】解:∵a∥b,∠1=30°,
∴∠ABC=∠1=30°,
由题可知:∠BAC=90°,
∴∠ABC+∠2=90°,
∴∠2=90°−30°=60°.
故答案为:60°.
【点评】本题考查平行线的性质,掌握平行线的性质是解题的关键.
13.(3分)若长方形的面积是2x3y4,宽为x2y,则它的长为 2xy3 .
【分析】根据长方形的面积等于长乘以宽列出算式计算即可.
【解答】解:由题意得它的长为2x3y4÷x2y=2xy3,
故答案为:2xy3.
【点评】本题考查了单项式除以单项式,熟练掌握其运算法则是解题的关键.
14.(3分)如图,在△ABC中,∠C=90°,AD是△ABC的一条角平分线,若CD=6,则点D到AB的距离为 6 .
【分析】根据角平分线上的点到角的两边的距离相等的性质可得点D到AB的距离DE长为等于CD的长,进行解答即可.
【解答】解:过D作DE⊥AB于E,
∵AD是∠BAC的角平分线,∠C=90°,
∴DE=CD,
∵CD=6,
∴DE=6,
故答案为:6.
【点评】本题主要考查了角平分线上的点到角的两边的距离相等的性质,是基础题,比较简单.
15.(3分)已知a、b为等腰△ABC的边长,且满足|a﹣5|+(b﹣11)2=0,则△ABC的底边长是 5 .
【分析】根据非负数的意义列出关于a、b的方程并求出a、b的值,再根据b是腰长和底边长两种情况讨论求解.
【解答】解:∵|a﹣5|+(b﹣11)2=0,
∴a﹣5=0,b﹣11=0,
解得:a=5,b=11,
又∵a,b是等腰△ABC的两边长,
∴当b是腰,a是底时,△ABC三边长分别为:11,11,5,
∴该等腰三角形的底边长是:5,
当a=5是腰,b=11是底时,△ABC三边长分别为:5,5,11,
∵5+5=10<11,
∴不满足三角形三边关系,应舍去.
故答案为:5.
【点评】本题考查了等腰三角形的性质、非负数的性质及三角形三边关系;解题主要利用了非负数的性质,分情况讨论求解时要注意利用三角形的三边关系对三边能否组成三角形做出判断.根据题意列出方程式正确解答本题的关键.
16.(3分)如图,在△ABC中,BC=8,S△ABC=40,点P是BC边上一动点,连接AP,在AP的上方作等边三角形APQ,则△APQ周长的最小值为 30 .
【分析】根据等边三角形的性质,得到△APQ周长=3AP,根据垂线段最短推出△APQ周长的最小值为3AP',再利用三角形的面积求出AP'即可.
【解答】解:∵△APQ是等边三角形,
∴AP=PQ=AQ,
∴△APQ周长=AP+PQ+AQ=3AP,
过点A作AP'⊥BC于点P',
则AP≥AP',
∴△APQ周长的最小值为3AP',
∵BC=8,S△ABC=40,
∴×8•AP'=40,
解得AP'=10,
∴△APQ周长的最小值为30,
故答案为:30.
【点评】本题考查等边三角形的性质,垂线段最短,三角形面积计算,掌握相关图形的性质和面积法是解题的关键.
三、解答题(共7道题,计52分,解答要写出过程)
17.(8分)(1);
(2)(3a2b)2÷(﹣3a3b)•(﹣2ab3).
【分析】(1)根据正整数指数幂,零指数幂的定义计算即可;
(2)先计算乘方,再计算乘除即可.
【解答】解:(1)原式=﹣1+1﹣
=﹣;
(2)原式=9a4b2÷3a3b•2ab3
=(9÷3×2)a4﹣3+1b2﹣1+3,
=6a2b4.
【点评】本题考查整式的混合运算,解题的关键是掌握整式的混合运算法则.
18.(5分)如图,在△ABC中,AB=AC,AD是BC边上的高.请用尺规作图法,在AD上求作一点P使得PA=PB=PC.(保留作图痕迹,不写作法)
【分析】作线段AB的垂直平分线,交AD于点P,结合线段垂直平分线的性质以及等腰三角形的性质可知,点P即为所求.
【解答】解:如图,作线段AB的垂直平分线,交AD于点P,
则PA=PB.
∵AB=AC,
∴△ABC为等腰三角形,
∴AD垂直平分BC,
∴PB=PC,
即PA=PB=PC,
则点P即为所求.
【点评】本题考查作图—复杂作图、线段垂直平分线的性质、等腰三角形的性质,熟练掌握线段垂直平分线的性质、等腰三角形的性质是解答本题的关键.
19.(6分)先化简,再求值:(2a﹣1)2+6a(a+1)﹣(3a﹣2)(3a+2),其中a2+2a﹣2024=0.
【分析】去括号,合并同类项,再利用整体代入的思想解决问题.
【解答】解:原式=4a2﹣4a+1+6a2+6a﹣(9a2﹣4)
=4a2﹣4a+1+6a2+6a﹣9a2+4
=a2+2a+5,
∵a2+2a﹣2024=0,
∴a2+2a=2024,
∴上式=2024+5=2029.
【点评】本题考查整式的混合运算,解题的关键是掌握整式的混合运算法则.
20.(7分)已知:如图,AB∥DE,AB=DE,AF=DC.求证:∠B=∠E.
【分析】由AF=DC,得AC=DF,由AB∥DE,得∠A=∠D,即可证△ABC≌△DEF(SAS),故∠B=∠E.
【解答】证明:∵AF=DC,
∴AF+CF=DC+CF,即AC=DF,
∵AB∥DE,
∴∠A=∠D,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠B=∠E.
【点评】本题考查三角形全等的判定与性质,解题的关键是掌握三角形全等的判定定理.
21.(8分)小明在学习完乘法公式后,发现完全平方公式经过适当的变形或数形结合,可以解决很多数学问题.
例如:若a+b=5,ab=6,求a2+b2的值.
解:∵a+b=5,ab=6,
∴(a+b)2=25,2ab=12,
∴a2+b2+2ab=25.
∴a2+b2=13.
(1)若m﹣n=3,mn=54,求m2+n2的值.
(2)请同学们根据上面的解题思路与方法,结合几何图形解决下列问题:如图,C是线段AB上的一点,分别以AC,BC为边向两边作正方形ACDE和正方形BCFG,设AB=10,两个正方形的面积和为52,求△FCA的面积.
【分析】(1)根据完全平方公式经过适当的变形计算即可;
(2)设AC=x,BC=y,由题意得:x2+y2=52,AB=AC+BC=x+y=10,根据(x+y)2=x2+y2+2xy,求得xy=24,因此△FCA的面积=×AC×BC=xy=×24=12.
【解答】解:(1)∵m﹣n=3,mn=54,
∴m2+n2=(m﹣n)2+2mn=32+2×54=117;
(2)设AC=x,BC=y,
由题意得:x2+y2=52,AB=AC+BC=x+y=10,
∴(x+y)2=x2+y2+2xy,
∴102=52+2xy,
∴xy=24,
∴△FCA的面积=×AC×BC=xy=×24=12.
【点评】本题考查的是因式分解的应用和完全平方公式的几何背景,熟练掌握上述知识点是解题的关键.
22.(8分)小玲和弟弟小亮分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步中途改为步行,到达图书馆恰好用30min.小亮骑自行车以300m/min的速度直接回家,两人离家的路程y(m)与各自离开出发地的时间x(min)之间的图象关系如图所示.
(1)家与图书馆之间的路程为 4000 m,小玲步行的速度为 100 m/min;
(2)求小玲和弟弟小亮途中相遇的时间.
【分析】(1)根据图象和“速度=路程÷时间”计算即可;
(2)根据“小亮离家的路程=家与图书馆的距离﹣小亮与图书馆的距离”写出他离家的路程y与时间x的关系式,并将y=0代入求出他到家的时间;根据“路程=速度×时间”求出当0≤x≤10和10<x≤30时,小玲离家的路程y与时间x的关系式;当二人相遇时,二人的函数值相等,列方程并求解即可.
【解答】解:(1)由图象可知,家与图书馆之间的路程为4000m,步行的速度为(4000﹣2000)÷(30﹣10)=100(m/min).
故答案为:4000,100.
(2)小亮离家的路程y与时间x的关系为y=4000﹣300x=﹣300x+4000,
当y=0时,得﹣300x+4000=0,
解得x=,
∴小亮离家的路程y与时间x的关系为y=﹣300x+4000(0≤x≤).
当0≤x≤10时,小玲跑步的速度为2000÷10=200(m/min),其离家的路程y与时间x的关系为y=200x;
当10<x≤30时,小玲离家的路程y与时间x的关系为y=2000+100(x﹣10)=100x+1000;
∴小玲离家的路程y与时间x的关系为y=.
当0≤x≤10时,若二人在此期间相遇,根据二人离家的距离相等,得﹣300x+4000=200x,解得x=8,
∴小玲和弟弟小亮于二人出发后8min时在途中相遇.
【点评】本题考查一次函数的应用,熟练掌握速度、时间、路程之间的数量关系是解题的关键.
23.(10分)发现问题
(1)已知,如图①,在四边形ABCD中,E在BC上,AE=DE,∠ABE=∠AED=∠ECD,若AB=5,BC=12,则BE= 7 .
探究问题
(2)如图②,已知长方形ABCD的周长为36,CD=10,点E为AD边上一点,EG⊥EF分别交AB于点G,交CD于点F,且EG=EF,求四边形BCFG的面积.
解决问题
(3)如图③,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB=13,以AB为边在其左上方作正方形ABEF,FD垂直于CA延长线于点D,连接AE,M、N分别为AE、BC上两动点,连接FM,BM,MN,当BM+MN的值最小时,求多边形EFMNB的面积.(注:四边相等,四个角是直角的四边形是正方形,正方形是轴对称图形,对角线是其一条对称轴)
【分析】(1)首先推导出∠BAE=∠CED,进而推导出△ABE≌△ECD(AAS),得到EC=AB=5,利用BE=BC﹣EC解答即可;
(2)求得AD=8,推导出∠DFE=∠AEG,进而得到△DFE≌△AEG(AAS),推导出DF=AE,DE=AG,推导出 ,S四边形ABCD=80,进而得到四边形BCFG的面积;
(3)连接FN,得到BM+MN=FM+MN≥FN,当F、M、N在同一直线上等号成立,且当FN⊥BC时,FN最小,进一步推导出△BAC≌△AFD(AAS),得到BC=AD=12,AC=FD=5,FN=17,CN=DF=5,计算出S四边形ACNF=55,S△ACB=30,最后利用S多边形EFMNB=S四边形ABEF+S△ACB﹣S四边形ACNF=144得到答案.
【解答】解:(1)∵∠BAE+∠BEA+∠ABE=180°,∠CED+∠BEA+∠AED=180°,∠ABE=∠AED,
∴∠BAE=∠CED,
∵∠ABE=∠ECD,AE=ED,
∴△ABE≌△ECD(AAS),
∴EC=AB=5,
∴BE=BC﹣EC=12﹣5=7,
故答案为:7;
(2)∵矩形ABCD的周长为36,CD=10,
∴,
∵∠DFE+∠DEF+∠D=180°,∠AEG+∠DEF+∠FEG=180°,∠D=∠FEG=90°,
∴∠DFE=∠AEG,
∵∠D=∠A=90°,FE=EG,
∴△DFE≌△AEG(AAS),
∴DF=AE,DE=AG,
∴S四边形ADFG=(DF+AG)•AD=(AE+DE),
∵S四边形ABCD=AD•CD=80,
∴S四边形BCFG=S四边形ABCD﹣S四边形ADFG=80﹣32=48,
即四边形BCFG的面积为48;
(3)连接FN,如图,
由题意知B、F关于AE对称,
∴MB=MF,
∴BM+MN=FM+MN≥FN,
当F、M、N在同一直线上等号成立,且当FN⊥BC时,FN最小,此时四边形CDFN是矩形,FN=CD,CN=DF,
∵AB=AF,∠C=∠D=∠BAF=90°,
由(2)可知∠BAC=∠AFD,
∴△BAC≌△AFD(AAS),
∴BC=AD=12,AC=FD=5,
∴FN=CD=AD+AC=12+5=17,CN=DF=5;
∵S四边形ABEF=AB•AB=169,
S四边形ACNF=(AC+FN)•CN=×(5+17)×5=55,S△ACB=AC•CB=12×5×12=30,
即当BM+MN最小时,多边形EFMNB的面积为:
S多边形EFMNB=S四边形ABEF+S△ACB﹣S四边形ACNF=144,
∴多边形EFMNB的面积为144.
【点评】本题属于四边形综合题,主要考查全等三角形的判定及应用,解答本题的关键是熟练掌握全等三角形判定定理,并结合三角形、矩形、正方形、梯形的面积公式进行解答.
x
﹣1
0
1
y
﹣1
1
3
x
﹣1
0
1
y
﹣1
1
3
相关试卷
这是一份2023-2024学年陕西省西安市碑林区西北工大附中七年级(下)第一次月考数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年陕西省西安市碑林区西北工大附中九年级(上)期末数学试卷(含解析),共23页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年陕西省西安市碑林区西北工大附中八年级(上)练习数学试卷(一)(含解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









