2024年新疆乌鲁木齐市第十三中学等中考二模考试数学试题

这是一份2024年新疆乌鲁木齐市第十三中学等中考二模考试数学试题，共28页。

A．+8B．﹣8C．±8D．﹣2
2．（4分）月球与地球的平均距离约为384000000米，数据384000000用科学记数法表示为（ ）
A．0.384×109B．3.84×108C．38.4×107D．384×106
3．（4分）下列运算结果正确的是（ ）
A．a3+a4＝a7B．a3•a3＝2a3
C．2a3•3a3＝6a9D．（﹣a2）3＝﹣a6
4．（4分）随着我国航天领域的快速发展，从“天宫一号”发射升空，到天和核心舱归位，我国正式迈入了“空间站时代”．下面是有关我国航天领域的图标，其图标既是轴对称图形又是中心对称图形的是（ ）
A．B．
C．D．
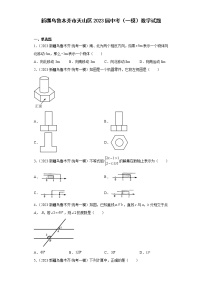
5．（4分）如图，在△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧，分别交AC、AB于点M，N，再分别以M，N为圆心，大于长为半径画弧，两弧交于点O，作射线AO，交BC于点E．已知CE＝3，AB＝8，△ABE的面积为（ ）
A．6B．9C．12D．18
6．（4分）“二十四节气”是中华上古农耕文明的智慧结晶，被国际气象界誉为“中国第五大发明”．小文购买了“二十四节气”主题邮票，他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐．小文将它们背面朝上放在桌面上（邮票背面完全相同），让小乐从中随机抽取一张（不放回），再从中随机抽取一张，则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是（ ）
A．B．C．D．
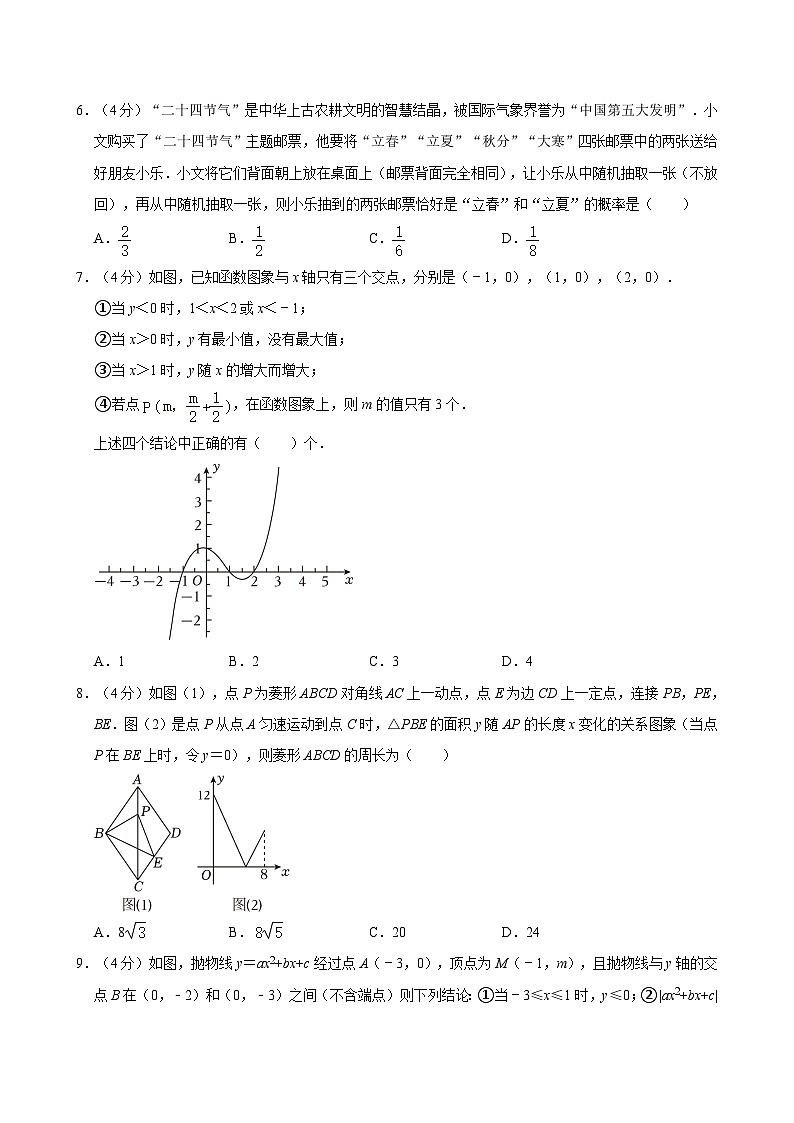
7．（4分）如图，已知函数图象与x轴只有三个交点，分别是（﹣1，0），（1，0），（2，0）．
①当y＜0时，1＜x＜2或x＜﹣1；
②当x＞0时，y有最小值，没有最大值；
③当x＞1时，y随x的增大而增大；
④若点，在函数图象上，则m的值只有3个．
上述四个结论中正确的有（ ）个．
A．1B．2C．3D．4
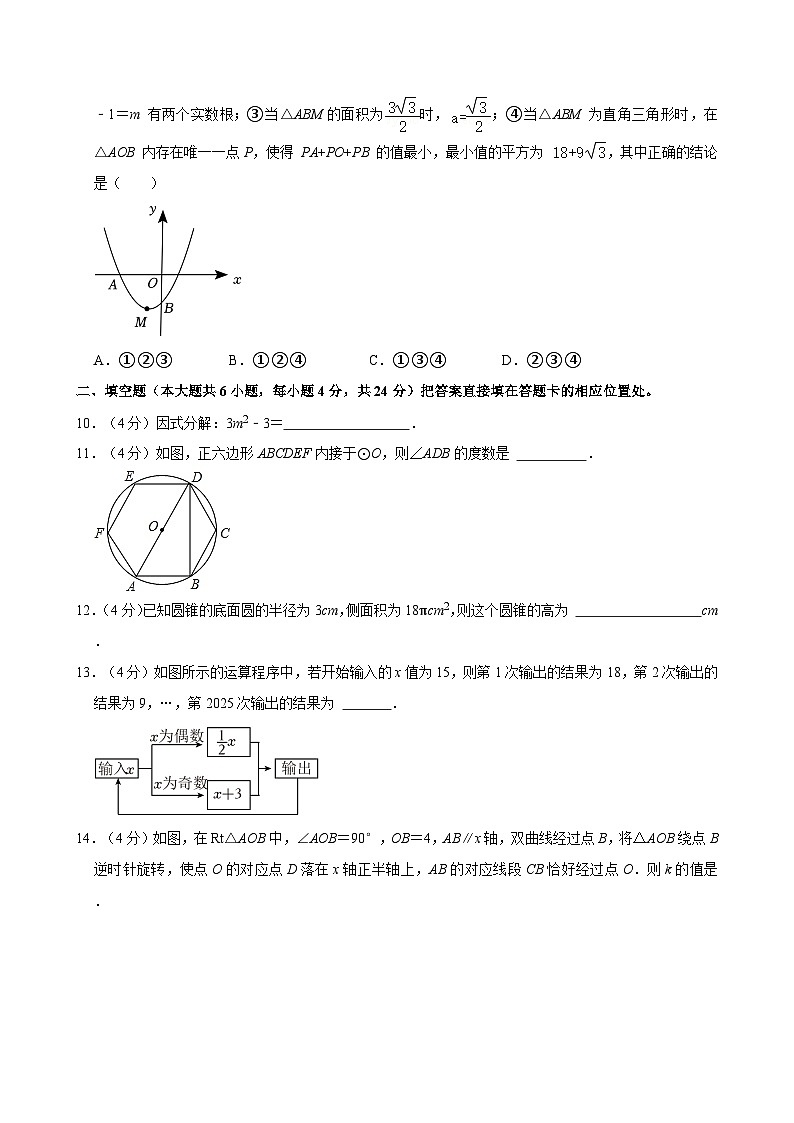
8．（4分）如图（1），点P为菱形ABCD对角线AC上一动点，点E为边CD上一定点，连接PB，PE，BE．图（2）是点P从点A匀速运动到点C时，△PBE的面积y随AP的长度x变化的关系图象（当点P在BE上时，令y＝0），则菱形ABCD的周长为（ ）
A．8B．C．20D．24
9．（4分）如图，抛物线y＝ax2+bx+c经过点A（﹣3，0），顶点为M（﹣1，m），且抛物线与y轴的交点B在（0，﹣2）和（0，﹣3）之间（不含端点）则下列结论：①当﹣3≤x≤1时，y≤0；②|ax2+bx+c|﹣1＝m 有两个实数根；③当△ABM的面积为时，；④当△ABM 为直角三角形时，在△AOB 内存在唯一一点P，使得 PA+PO+PB 的值最小，最小值的平方为 ，其中正确的结论是（ ）
A．①②③B．①②④C．①③④D．②③④
二、填空题（本大题共6小题，每小题4分，共24分）把答案直接填在答题卡的相应位置处。
10．（4分）因式分解：3m2﹣3＝ ．
11．（4分）如图，正六边形ABCDEF内接于⊙O，则∠ADB的度数是 ．
12．（4分）已知圆锥的底面圆的半径为3cm，侧面积为18πcm2，则这个圆锥的高为 cm．
13．（4分）如图所示的运算程序中，若开始输入的x值为15，则第1次输出的结果为18，第2次输出的结果为9，…，第2025次输出的结果为 ．
14．（4分）如图，在Rt△AOB中，∠AOB＝90°，OB＝4，AB∥x轴，双曲线经过点B，将△AOB绕点B逆时针旋转，使点O的对应点D落在x轴正半轴上，AB的对应线段CB恰好经过点O．则k的值是 ．
15．（4分）如图，矩形ABCO的顶点A，C分别在x轴、y轴上，点B的坐标为（4，3），⊙M是△AOC的内切圆，点N，点P分别是⊙M，x轴上的动点，则BP+PN的最小值是 ．
三、解答题（本大题共8小题，共90分）解答时应在答题卡的相应位置处写出文字说明、证明过程或演算过程。
16．（12分）（1）计算：|﹣|﹣2sin60°+（）﹣1+（2024﹣π）0；
（2）解分式方程：．
17．（10分）解不等式组：，并写出最小整数解．
18．（10分）如图，已知AB∥DE，AB＝DE，AC＝FD，∠CEF＝90°．
（1）求证：△ABF≌△DEC；
（2）求证：四边形BCEF是矩形．
19．（10分）3月14日是国际数学日，“数学是打开科学大门的钥匙”为进一步提高学生学习数学的兴趣．某校开展了一次数学趣味知识竞赛，并从男、女生中各随机抽取了20名学生的成绩（满分100分，成绩得分用x（分）表示，共分为五组：A．0≤x＜60；B．60≤x＜70；C．70≤x＜80；D．80≤x＜90；E．90≤x≤100；其中x≥80记为优秀），相关数据统计、整理如下：
男生被抽取的学生竞赛成绩：52，58，58，60，64，70，72，74，74，76，76，78，80，86，86，86，88，90，94，98．
女生被抽取的学生竞赛成绩中，C组的具体分数为：70，72，74，76，76，76，78，78．
男、女生被抽取的竞赛成绩统计表：
请根据以上信息，解答下列问题：
（1）填空：a＝ ，b＝ ，m＝ ；
（2）根据以上数据分析，从一个方面评价该校男、女生本届数学趣味知识竞赛成绩谁更优异？请说明理由（写出一条理由即可）；
（3）该校共有3000人，请你估计该校学生中竞赛成绩优秀的有多少人？
20．（10分）“游张家界山水，逛七十二奇楼”成为今年旅游新特色．某数学兴趣小组用无人机测量奇楼AB的高度，测量方案如图：先将无人机垂直上升至距水平地面225m的P点，测得奇楼顶端A的俯角为15°，再将无人机沿水平方向飞行200m到达点Q，测得奇楼底端B的俯角为45°，求奇楼AB的高度．（结果精确到1m，参考数据：sin15°≈0.26，cs15°≈0.97，tan15°≈0.27）
21．（12分）加强劳动教育，落实五育并举．某中学在当地政府的支持下，建成了一处劳动实践基地．2024年计划将其中1000m2的土地全部种植甲乙两种蔬菜．经调查发现：甲种蔬菜种植成本y（单位：元/m2）与其种植面积x（单位：m2）的函数关系如图所示，其中200≤x≤700，乙种蔬菜的种植成本为50元/m2．
（1）求甲种蔬菜种植成本y与其种植面积x之间的函数解析式；
（2）设2024年甲乙两种蔬菜总种植成本为W元，如何分配两种蔬菜的种植面积，使W最小？
22．（12分）如图，在△ABC中，AC＝BC，以BC为直径作⊙O，交AC于点F，过C点作CD⊥AC交AB延长线于点D，E为CD上一点，且EB＝ED．
（1）求证：BE为⊙O的切线；
（2）若AF＝2，tanA＝2，求BE的长．
23．（14分）[问题探究]
（1）如图1，在正方形ABCD中，对角线AC、BD相交于点O．在线段AO上任取一点P（端点除外），连接PD、PB．
①求证：PD＝PB；
②将线段DP绕点P逆时针旋转，使点D落在BA的延长线上的点Q处．当点P在线段AO上的位置发生变化时，∠DPQ的大小是否发生变化？请说明理由；
③探究AQ与OP的数量关系，并说明理由．
[迁移探究]
如图2，将正方形ABCD换成菱形ABCD，且∠ABC＝60°，其他条件不变．试探究AQ与CP的数量关系，并说明理由．
2024年新疆乌鲁木齐十三中等校中考数学二模试卷
参考答案与试题解析
一、选择题（本大题共9小题，每小题4分，共36分）每题所给的四个选项中只有一项是符合题目要求的，请将选项的代号字母填在答卷的相应位置处。
1．（4分）中国是最早采用正负数表示相反意义的量的国家．某仓库运进小麦6吨，记为+6吨，那么仓库运出小麦8吨应记为（ ）吨．
A．+8B．﹣8C．±8D．﹣2
【解答】解：∵仓库运进小麦6吨，记为+6吨，
∴仓库运出小麦8吨应记为﹣8吨，
故选：B．
2．（4分）月球与地球的平均距离约为384000000米，数据384000000用科学记数法表示为（ ）
A．0.384×109B．3.84×108C．38.4×107D．384×106
【解答】解：384000000＝3.84×108．
故选：B．
3．（4分）下列运算结果正确的是（ ）
A．a3+a4＝a7B．a3•a3＝2a3
C．2a3•3a3＝6a9D．（﹣a2）3＝﹣a6
【解答】解：A、不是同类项不能合并，原计算错误，不符合题意；
B、a3•a3＝a6，原计算错误，不符合题意；
C、2a3•3a3＝6a6，原计算错误，不符合题意；
D、（﹣a2）3＝﹣a6，原计算正确，符合题意；
故选：D．
4．（4分）随着我国航天领域的快速发展，从“天宫一号”发射升空，到天和核心舱归位，我国正式迈入了“空间站时代”．下面是有关我国航天领域的图标，其图标既是轴对称图形又是中心对称图形的是（ ）
A．B．
C．D．
【解答】解：A、原图不是轴对称图形，不是中心对称图形，故此选项不合题意；
B、原图既是中心对称图形，又是轴对称图形，故此选项符合题意；
C、原图是轴对称图形，不是中心对称图形，故此选项不合题意；
D、原图不是中心对称图形，也不是轴对称图形，故此选项不合题意；
故选：B．
5．（4分）如图，在△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧，分别交AC、AB于点M，N，再分别以M，N为圆心，大于长为半径画弧，两弧交于点O，作射线AO，交BC于点E．已知CE＝3，AB＝8，△ABE的面积为（ ）
A．6B．9C．12D．18
【解答】解：由基本作图得到AE平分∠BAC，
∴点E为AC和AB的距离相等，
∴点E到AB的距离等于AC，即点E到AB的距离为3，
∴S△ABE＝×8×3＝12．
故选：C．
6．（4分）“二十四节气”是中华上古农耕文明的智慧结晶，被国际气象界誉为“中国第五大发明”．小文购买了“二十四节气”主题邮票，他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐．小文将它们背面朝上放在桌面上（邮票背面完全相同），让小乐从中随机抽取一张（不放回），再从中随机抽取一张，则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是（ ）
A．B．C．D．
【解答】解：设立春用A表示，立夏用B表示，秋分用C表示，大寒用D表示，树状图如下，
由上可得，一共有12种可能性，其中小乐抽到的两张邮票恰好是“立春”和“立夏”的可能性2种，
∴小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是＝，
故选：C．
7．（4分）如图，已知函数图象与x轴只有三个交点，分别是（﹣1，0），（1，0），（2，0）．
①当y＜0时，1＜x＜2或x＜﹣1；
②当x＞0时，y有最小值，没有最大值；
③当x＞1时，y随x的增大而增大；
④若点，在函数图象上，则m的值只有3个．
上述四个结论中正确的有（ ）个．
A．1B．2C．3D．4
【解答】解：根据函数图象可知：
①当y＜0时，1＜x＜2或x＜﹣1，正确；
②当x＞0时，y有最小值，没有最大值，正确；
③当x＞1时，y随x的增大而增大，错误；
④如图，结合函数图象可知：
若点同时在函数y＝图象上，则m的值有3个，故④正确．
故上述四个结论中正确的有3个．
故选：C．
8．（4分）如图（1），点P为菱形ABCD对角线AC上一动点，点E为边CD上一定点，连接PB，PE，BE．图（2）是点P从点A匀速运动到点C时，△PBE的面积y随AP的长度x变化的关系图象（当点P在BE上时，令y＝0），则菱形ABCD的周长为（ ）
A．8B．C．20D．24
【解答】解：由图象可知：当x＝0时，即点P与点A重合，此时S△ABE＝12，
∴S菱形ABCD＝2S△ABE＝24，
当x＝8时，此时点P与点C重合，即AC＝8，连接BD，交AC于点O，
则：BD⊥AC，OA＝OC＝4，OB＝OD，
∴，
∴BD＝6，
∴OB＝OD＝3，
∴，
∴菱形ABCD的周长为4×5＝20；
故选：C．
9．（4分）如图，抛物线y＝ax2+bx+c经过点A（﹣3，0），顶点为M（﹣1，m），且抛物线与y轴的交点B在（0，﹣2）和（0，﹣3）之间（不含端点）则下列结论：①当﹣3≤x≤1时，y≤0；②|ax2+bx+c|﹣1＝m 有两个实数根；③当△ABM的面积为时，；④当△ABM 为直角三角形时，在△AOB 内存在唯一一点P，使得 PA+PO+PB 的值最小，最小值的平方为 ，其中正确的结论是（ ）
A．①②③B．①②④C．①③④D．②③④
【解答】解：①∵抛物线y＝ax2+bx+c经过点A（﹣3，0），顶点为M（﹣1，m），
∴抛物线y＝ax2+bx+c的对称轴为直线x＝﹣1，
∴抛物线y＝ax2+bx+c与x轴的另一个交点坐标为（1，0），
∵抛物线y＝ax2+bx+c的开口向上，
∴当﹣3≤x≤1时，y≤0，
故①正确；
②方程|ax2+bx+c|﹣1＝m 可变形为方程|ax2+bx+c|＝m+1，
因此|ax2+bx+c|﹣1＝m 有两个实数根相当于函数y＝|ax2+bx+c|的图象与函数y＝m+1的图象有两个交点，
画出函数图象如下：
故②正确；
③将（﹣3，0），（1，0）代入y＝ax2+bx+c，
得，
解得：，
∴y＝ax2+2ax﹣3a＝a（x+1）2﹣4a，
∴抛物线的顶点为M（﹣1，﹣4a），
设抛物线对称轴交x轴于H，如图，
则H（﹣1，0），
∴AH＝﹣1﹣（﹣3）＝2，MH＝4a，OH＝1，
∵B（0，﹣3a），
∴OB＝3a，
∴S△ABM＝S△AMH+S梯形BMHO﹣S△AOB＝•AH•MH+•（MH+OB）•OH﹣OA•OB＝×2×4a+×（4a+3a）×1﹣×3×3a＝3a，
∵S△ABM＝，
∴3a＝
∴a＝，
故③正确；
④如图，过点A、M分别作y轴、x轴的平行线交于点C，连接AM、AB、BM，
则四边形ACDO是矩形，
∴∠C＝∠BDM＝∠AOB＝90°，
∵A（﹣3，0），B（0，﹣3a），M（﹣1，﹣4a），
∴AC＝OD＝4a，OA＝CD＝3，OB＝3a，BD＝a，DM＝1，CM＝2，
∵△ABM为直角三角形，有三种情况：∠BAM＝90°或∠AMB＝90°或∠ABM＝90°，
显然∠BAM＜90°，
∴只能∠AMB＝90°或∠ABM＝90°，
若∠AMB＝90°，则∠AMC+∠BMD＝90°，
∵AC∥OD，OA∥DC，
∴四边形ACDO是平行四边形，
∵∠AOD＝90°，
∴四边形ACDO是矩形，
∴∠C＝∠BDM＝∠AOB＝90°，
∴∠AMC+∠MAC＝90°，
∴△AMC∽△MBD，
∴＝，即，
∴a2＝，
∵a＞0，
∴a＝；
若∠ABM＝90°，则∠ABO+∠MBD＝90°，
∵∠AOB＝∠BDM＝90°，
∴∠ABO+∠BAO＝90°，
∴∠MBD＝∠BAO，
∴△ABO∽△BMD，
∴，即，
∴a2＝1，
∵a＞0，
∴a＝1；
∵点B在（0，﹣2）与（0，﹣3）之间（不含端点），
∴﹣3＜﹣3a＜﹣2，
解得＜a＜1，
∴a＝，
∴OB＝，AB2＝，
如图，将△BPA绕点B逆时针旋转60°得到△BP′A′，连接PP′，过点A′作A′T⊥x轴于点T，作A′Q⊥y轴于点Q，
∴BP＝BP′，PA＝P′A′，∠PBP′＝∠ABA′＝60°，
∴△PBP′和△ABA′是等边三角形，
∴BP＝PP′，AA′2＝A′B2＝AB2＝，
∴PA+PO+PB＝P′A′+PO+PP′≥OA′，
∴当点O、P、P′、A′共线时，PA+PO+PB值最小，最小值为OA′，
此时∠APB＝∠APO＝∠BPO＝120°，
设A′（m，n），
则A′T＝﹣n，AT＝﹣3﹣m，A′Q＝﹣m，BQ＝﹣n﹣，
在Rt△AA′T中，
由勾股定理，得AT2+A′T2＝AA′2，
在Rt△BA′Q中，
由勾股定理，得BQ2+A′Q2＝A′B2，
即，
解得，
∴OA′2＝m2+n2＝（）2+（）2＝≠，
故④错误；
综上，正确的有①②③．
故选：A．
二、填空题（本大题共6小题，每小题4分，共24分）把答案直接填在答题卡的相应位置处。
10．（4分）因式分解：3m2﹣3＝ 3（m﹣1）（m+1） ．
【解答】解：原式＝3（m2﹣1）＝3（m﹣1）（m+1），
故答案为：3（m﹣1）（m+1）．
11．（4分）如图，正六边形ABCDEF内接于⊙O，则∠ADB的度数是 30° ．
【解答】解：连接OB，
∵六边形ABCDEF是正六边形，
∴∠AOB＝＝60°，
∴∠ADB＝∠AOB＝×60°＝30°．
故答案为：30．
12．（4分）已知圆锥的底面圆的半径为3cm，侧面积为18πcm2，则这个圆锥的高为 cm．
【解答】解：由题意得：圆锥的母线长为l＝＝6（cm），
∴圆锥的高为h＝＝3（cm）；
故答案为：．
13．（4分）如图所示的运算程序中，若开始输入的x值为15，则第1次输出的结果为18，第2次输出的结果为9，…，第2025次输出的结果为 3 ．
【解答】解：依题意，第3次输出的结果为：9+3＝12，
第4次输出的结果为：，
第5次输出的结果为：，
第6次输出的结果为：3+3＝6，
第7次输出的结果为：，
第8次输出的结果为：3+3＝6，
…，
∴从4次开始，每次输出的结果都是6、3、6、3、…，
∴第2025次输出的结果为3．
故答案为：3．
14．（4分）如图，在Rt△AOB中，∠AOB＝90°，OB＝4，AB∥x轴，双曲线经过点B，将△AOB绕点B逆时针旋转，使点O的对应点D落在x轴正半轴上，AB的对应线段CB恰好经过点O．则k的值是 4 ．
【解答】解：∵AB∥x轴，
∴∠ABO＝∠BOD，
∵∠ABO＝∠CBD，
∴∠BOD＝∠OBD，
∵OB＝BD，
∴∠BOD＝∠BDO，
∴△BOD是等边三角形，
∴∠BOD＝60°，
∴B（2，2），
∵双曲线y＝经过点B，
∴k＝2×2＝4．
故答案为：4．
15．（4分）如图，矩形ABCO的顶点A，C分别在x轴、y轴上，点B的坐标为（4，3），⊙M是△AOC的内切圆，点N，点P分别是⊙M，x轴上的动点，则BP+PN的最小值是 4 ．
【解答】解：作点B关于x轴的对称点B′，连接MB′，交⊙M于点N，交x轴于点P，
过点M作MQ⊥x轴，交x轴于点E，过点B′作B′Q⊥MQ，
∵点B与点B′关于x轴对称，
∴PB+PN＝PB′+PN，
当N、P、B’在同一直线上且经过点M时取最小值．
在Rt△ABC中，AC＝＝5，
由⊙M是△AOC的内切圆，设⊙M的半径为r，
∴S△AOC＝（3r+4r+5r）＝×3×4，
解得r＝1，
∴ME＝MN＝1，
∴QB′＝4﹣1＝3，QM＝3+1＝4，
∴MB′＝5，
∴PB′+PN＝5﹣1＝4，
即PB+PN最小值为4，
故答案为：4．
三、解答题（本大题共8小题，共90分）解答时应在答题卡的相应位置处写出文字说明、证明过程或演算过程。
16．（12分）（1）计算：|﹣|﹣2sin60°+（）﹣1+（2024﹣π）0；
（2）解分式方程：．
【解答】解：（1）原式＝﹣2×+4+1
＝﹣+4+1
＝5；
（2）原方程去分母得：2x+3﹣2（x﹣2）＝1﹣x，
整理得：7＝1﹣x，
解得：x＝﹣6，
检验：当x＝﹣6时，x﹣2≠0，
故原方程的解为x＝﹣6．
17．（10分）解不等式组：，并写出最小整数解．
【解答】解：，
解不等式①得：x≤8，
解不等式②得：，
∴不等式组的解集为，
∴不等式组的最小整数解为2．
18．（10分）如图，已知AB∥DE，AB＝DE，AC＝FD，∠CEF＝90°．
（1）求证：△ABF≌△DEC；
（2）求证：四边形BCEF是矩形．
【解答】证明：（1）∵AB∥DE，
∴∠A＝∠D，
∵AC＝FD，
∴AC﹣CF＝DF﹣CF，
即AF＝CD，
在△ABF与△DEC中，
，
∴△ABF≌△DEC（SAS）；
（2）∵△ABF≌△DEC，
∴EC＝BF，∠ECD＝∠BFA，
∴∠ECF＝∠BFC，
∴EC∥BF，
∵∠CEF＝90°，
∴四边形BCEF是矩形．
19．（10分）3月14日是国际数学日，“数学是打开科学大门的钥匙”为进一步提高学生学习数学的兴趣．某校开展了一次数学趣味知识竞赛，并从男、女生中各随机抽取了20名学生的成绩（满分100分，成绩得分用x（分）表示，共分为五组：A．0≤x＜60；B．60≤x＜70；C．70≤x＜80；D．80≤x＜90；E．90≤x≤100；其中x≥80记为优秀），相关数据统计、整理如下：
男生被抽取的学生竞赛成绩：52，58，58，60，64，70，72，74，74，76，76，78，80，86，86，86，88，90，94，98．
女生被抽取的学生竞赛成绩中，C组的具体分数为：70，72，74，76，76，76，78，78．
男、女生被抽取的竞赛成绩统计表：
请根据以上信息，解答下列问题：
（1）填空：a＝ 77 ，b＝ 86 ，m＝ 40 ；
（2）根据以上数据分析，从一个方面评价该校男、女生本届数学趣味知识竞赛成绩谁更优异？请说明理由（写出一条理由即可）；
（3）该校共有3000人，请你估计该校学生中竞赛成绩优秀的有多少人？
【解答】解：（1）女生竞赛成绩从小到大排列后，处在中间位置的两个数的平均数为a＝（76+78）÷2＝77（分），
因此中位数是7（7分），即a＝77，
男生竞赛成绩出现最多的是86，
因此男生竞赛成绩的众数86，即b＝86；
m＝（1﹣10%﹣10%﹣）×100＝40，
故答案为：77，86，40；
（2）女生本届数学趣味知识竞赛成绩更优异，
理由为：女生本届数学趣味知识竞赛成绩的中位数较高；
（3）3000×40%＝1200（人），
答：估计该校学生中竞赛成绩优秀的有1200人．
20．（10分）“游张家界山水，逛七十二奇楼”成为今年旅游新特色．某数学兴趣小组用无人机测量奇楼AB的高度，测量方案如图：先将无人机垂直上升至距水平地面225m的P点，测得奇楼顶端A的俯角为15°，再将无人机沿水平方向飞行200m到达点Q，测得奇楼底端B的俯角为45°，求奇楼AB的高度．（结果精确到1m，参考数据：sin15°≈0.26，cs15°≈0.97，tan15°≈0.27）
【解答】解：延长BA交PQ的延长线于C，
则∠ACQ＝90°，
由题意得，BC＝225m，PQ＝200m，
在Rt△BCQ中，∠BQC＝45°，
∴CQ＝BC＝225m，
∴PC＝PQ+CQ＝425（m），
在Rt△PCA中，tan∠APC＝tan15°＝，
∴AC＝114.75m，
∴AB＝BC﹣AC＝225﹣114.75＝110.25≈110（m），
答：奇楼AB的高度约为110m．
21．（12分）加强劳动教育，落实五育并举．某中学在当地政府的支持下，建成了一处劳动实践基地．2024年计划将其中1000m2的土地全部种植甲乙两种蔬菜．经调查发现：甲种蔬菜种植成本y（单位：元/m2）与其种植面积x（单位：m2）的函数关系如图所示，其中200≤x≤700，乙种蔬菜的种植成本为50元/m2．
（1）求甲种蔬菜种植成本y与其种植面积x之间的函数解析式；
（2）设2024年甲乙两种蔬菜总种植成本为W元，如何分配两种蔬菜的种植面积，使W最小？
【解答】解：（1）当200≤x≤600时，设y＝kx+b，
由图象可得：，
解得；
∴y＝x+10（200≤x≤600）；
当600＜x≤700时，y＝40；
∴y＝；
（2）①当200≤x≤600时，W＝x（x+10）+50（1000﹣x）＝x2﹣40x+50000＝（x﹣400）2+42000，
∴抛物线对称轴为直线x＝400，
∴当x＝400时，W取最小值42000元；
②当600＜x≤700时，W＝40x+50（1000﹣x）＝﹣10x+50000，
∴当x＝700时，W取最小值为﹣10×700+50000＝43000（元）；
∵42000＜43000，
∴甲种蔬菜种植400m2，乙种蔬菜种植600m2，W最小为42000元．
22．（12分）如图，在△ABC中，AC＝BC，以BC为直径作⊙O，交AC于点F，过C点作CD⊥AC交AB延长线于点D，E为CD上一点，且EB＝ED．
（1）求证：BE为⊙O的切线；
（2）若AF＝2，tanA＝2，求BE的长．
【解答】（1）证明：∵AC＝BC，
∴∠CAB＝∠ABC，
∵EB＝ED，
∴∠EBD＝∠D．
∵CD⊥AC，
∴∠A+∠D＝90°，
∴∠ABC+∠EBD＝90°，
∴∠CBE＝180°﹣（∠ABC+∠EBD）＝90°．
∴OB⊥BE，
∵OB是⊙O的半径，
∴BE为⊙O的切线；
（2）解：设CD与⊙O交于点G，连接BF，BG，如图，
∵BC为⊙O的直径，
∵∠CFB＝∠CGB＝90°，
∵∠ACD＝90°，
∴四边形CFBG为矩形．
∴BG＝FC．
在Rt△AFB中，
∵AF＝2，tanA＝2＝，
∴BF＝4．
设AC＝BC＝x，则CF＝x﹣2．
∵CF2+BF2＝BC2，
∴（x﹣2）2+42＝x2，
解得：x＝5，
∴FC＝3，BC＝5．
∴BG＝3．
∵∠CBE＝90°，BG⊥CE，
∴△CBG∽△BGE．
∴，
∴，
∴EG＝．
∴BE＝＝．
23．（14分）[问题探究]
（1）如图1，在正方形ABCD中，对角线AC、BD相交于点O．在线段AO上任取一点P（端点除外），连接PD、PB．
①求证：PD＝PB；
②将线段DP绕点P逆时针旋转，使点D落在BA的延长线上的点Q处．当点P在线段AO上的位置发生变化时，∠DPQ的大小是否发生变化？请说明理由；
③探究AQ与OP的数量关系，并说明理由．
[迁移探究]
（2）如图2，将正方形ABCD换成菱形ABCD，且∠ABC＝60°，其他条件不变．试探究AQ与CP的数量关系，并说明理由．
【解答】（1）①证明：∵四边形ABCD是正方形，
∴CD＝CB，∠DCA＝∠BCA＝45°．
∵CP＝CP，
∴△DCP≌△BCP，
∴PD＝PB；
②解：∠DPQ的大小不发生变化，∠DPQ＝90°；
理由：作PM⊥AB，PN⊥AD，垂足分别为点M、N，如图，
∵四边形ABCD是正方形，
∴∠DAC＝∠BAC＝45°，∠DAB＝90°，
∴四边形AMPN是矩形，PM＝PN，
∴∠MPN＝90°．
.∵PD＝PQ，PM＝PN，
∴Rt△DPN≌Rt△QPM（HL），
∴∠DPN＝∠QPM，
∴∠QPN+∠QPM＝90°．
∴∠QPN+∠DPN＝90°，即∠DPQ＝90°；
③解：AQ＝OP；
理由：作PE⊥AO交AB于点E，作EF⊥OB于点F，如图，
∵四边形ABCD是正方形，
∴∠BAC＝45°，∠AOB＝90°，
∴∠AEP＝45°，四边形OPEF是矩形，
∴∠PAE＝∠PEA＝45°，EF＝OP，
∴PA＝PE，
∵PD＝PB，PD＝PQ，
∴PQ＝PB，
作PM⊥AE于点M，
则QM＝BM，AM＝EM，
∴AQ＝BE，
∵∠EFB＝90°，∠EBF＝45°，
∴BE＝EF，
∴AQ＝OP；
（2）解：AQ＝CP；
理由：四边形ABCD是菱形，∠ABC＝60°，
∴AB＝BC，AC⊥BD，DO＝BO，
∴△ABC是等边三角形，AC垂直平分BD，
∴∠BAC＝60°，PD＝PB，
∵PD＝PQ，
∴PQ＝PB，
作PE∥BC交AB于点E，EG∥AC交BC于点G，如图，
则四边形PEGC是平行四边形，∠GEB＝∠BAC＝60°，∠AEP＝∠ABC＝60°，
∴EG＝PC，△APE，△BEG都是等边三角形，
∴BE＝EG＝PC，
作PM⊥AB于点M，则QM＝MB，AM＝EM，
∴QA＝BE，
∴AQ＝CP．性别
男生
女生
平均数
76
76
中位数
76
a
众数
b
87
优秀率
40%
m%
性别
男生
女生
平均数
76
76
中位数
76
a
众数
b
87
优秀率
40%
m%