



所属成套资源:【专项复习】高考数学 立体几何与空间向量(题型专练)
【专项复习】高考数学专题04 点到平面的距离(题型训练).zip
展开
这是一份【专项复习】高考数学专题04 点到平面的距离(题型训练).zip,文件包含专项复习高考数学专题04点到平面的距离题型训练原卷版docx、专项复习高考数学专题04点到平面的距离题型训练解析版docx等2份试卷配套教学资源,其中试卷共53页, 欢迎下载使用。
\l "_Tc32608" 二、典型题型 PAGEREF _Tc32608 \h 2
\l "_Tc9471" 题型一:等体积法求点到平面的距离 PAGEREF _Tc9471 \h 2
\l "_Tc29999" 题型二:利用向量法求点到平面的距离 PAGEREF _Tc29999 \h 10
\l "_Tc29092" 三、专项训练 PAGEREF _Tc29092 \h 16
一、必备秘籍
1、等体积法求点到平面的距离
(1)当点到面的距离那条垂线不好作或找时,利用等体积法可以间接求点到面的距离,从而快速解决体积问题,是一种常用数学思维方法
(2)在用变换顶点求体积时,变换顶点的原则是能在图象中直接找到求体积所用的高,有时单一靠棱锥四个顶点之间来变换顶点无法达到目的时,还可以利用平行关系(线面平行,面面平行)转换顶点,如当线面平行时,线上任意一点到平面的距离是相等的,同理面面平行也可以变换顶点
2、利用向量法求点到平面的距离
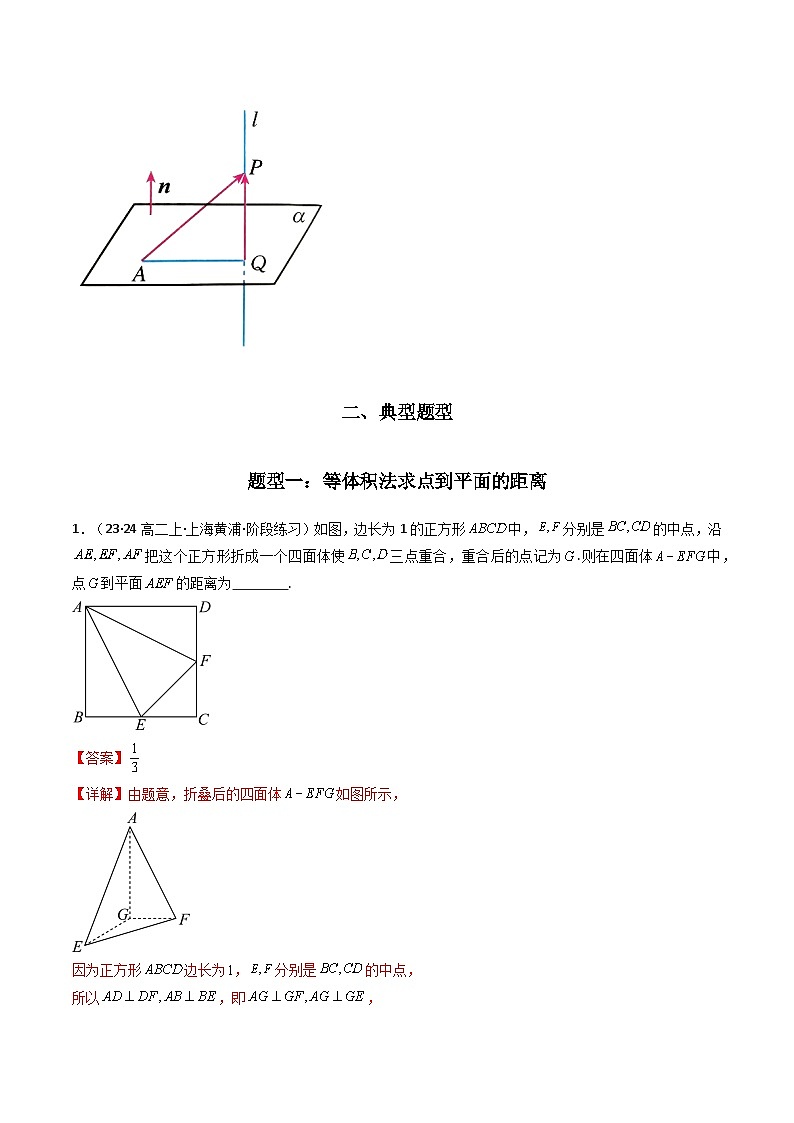
如图,已知平面的法向量为,是平面内的定点,是平面外一点.过点作平面的垂线,交平面于点,则是直线的方向向量,且点到平面的距离就是在直线上的投影向量的长度.
二、典型题型
题型一:等体积法求点到平面的距离
1.(23·24高二上·上海黄浦·阶段练习)如图,边长为1的正方形中,分别是的中点,沿把这个正方形折成一个四面体使三点重合,重合后的点记为.则在四面体中,点到平面的距离为 .
【答案】
【详解】由题意,折叠后的四面体如图所示,
因为正方形边长为,分别是的中点,
所以,即,
又平面,所以平面,
同时由,得,
又,
所以,
,
设到平面的距离为,
则,即,解得.
故答案为:.
2.(23·24高二上·上海虹口·期中)如图,已知点P在圆柱的底面圆O的圆周上,,圆O的直径,圆柱的高.
(1)求圆柱的体积;
(2)求点A到平面的距离.
【答案】(1)
(2)
【详解】(1)由已知可得,圆柱的底面半径,圆柱的高,
圆柱体积为:;
(2)设点到平面的距离为,
在等腰中,由,则,
为直径,,
在中,,
则,
由底面,底面,所以,
又,平面,所以平面,
平面,
故,
, ,
由等体积法,得,
解得:.
即点到平面的距离为.
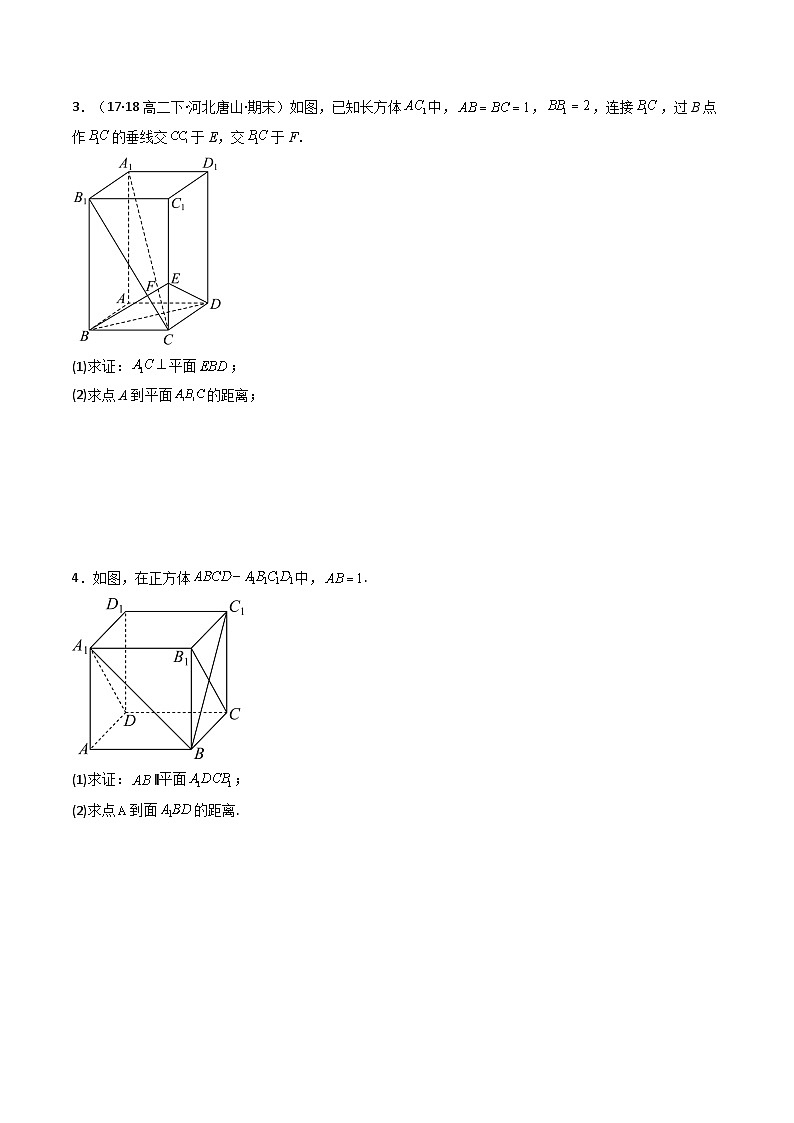
3.(17·18高二下·河北唐山·期末)如图,已知长方体中,,,连接,过B点作的垂线交于E,交于F.
(1)求证:平面;
(2)求点A到平面的距离;
【答案】(1)证明见解析
(2)
【详解】(1)证明:根据题意,平面,平面,得,
又(已知),平面,平面,,
所以平面,得.
同理,平面,得.
因为平面,平面,,,,
所以平面.
(2)因为平面,所以点A到平面的距离等于点B到平面的距离,设为d,
因为,,即,,
所以,.
故点A到平面的距离等于.
4.如图,在正方体中,.
(1)求证:∥平面;
(2)求点到面的距离.
【答案】(1)答案见详解
(2)
【详解】(1)∵∥, 平面,平面,
∴∥平面
(2)连接,设点到面的距离为,
由已知可得,
由正方体的性质可知平面,则,
∵,
∴,解得,
即点到面的距离为.
5.(23·24高二上·江西九江·阶段练习)如图所示的五边形中是矩形,,沿折叠成四棱锥.
(1)从条件①;②;③中任选两个作为补充条件,证明:平面平面:
(2)在(1)的条件下,求点到平面的距离.
【答案】(1)证明见解析
(2)
【详解】(1)选条件①②:
证明:由题意知,,,所以,
在中,,,则,,
又因为为矩形,,则,所以,
在中,,由余弦定理可得,解得,
所以,即,
又因为,、平面,
所以平面,
又因为平面,
所以平面平面.
选条件①③:
证明:由题意知,,,所以,
在中,,,则,,
又因为为矩形,,则,所以,
又,所以,即,
又因为,、平面,
所以平面,
又因为平面,
所以平面平面.
选条件②③:
证明:由题意知,,,所以,
在中,,,,
由余弦定理可得,解得,
所以,即,
又因为,、平面,
所以平面,
又因为平面,
所以平面平面.
(2)因为,平面,平面,
所以平面,
又,
所以点到平面的距离等于点到平面的距离.
由(1)知,平面,,
又,,
所以,,
所以,即,
所以,
在中,,,则,
所以在中,由余弦定理得,则,
所以,
设点到平面的距离为,则点到平面的距离也为,
由可得,即,解得,
故点到平面的距离为.
6.(23·24高三上·上海浦东新·阶段练习)如图,在四棱锥中,底面是矩形,其中,,底面,,为的中点,为的中点.
(1)证明:直线平面;
(2)求点到平面的距离.
【答案】(1)证明见解析
(2)
【详解】(1)证明:
如上图,取中点,连接、,
∵为的中点,为的中点,为的中点,
∴在矩形中,在中,
又∵平面,平面,平面,平面,
∴平面,平面,
又∵平面,平面,,
∴平面平面,
又∵平面,∴平面.
(2)解:
如上图,连接,由题意,,,,
∵底面,平面,平面,
∴,则是等腰直角三角形,
∴,
∵矩形中,,平面,平面,
∴平面,又∵平面,
∴,则是直角三角形,,
∴.
∵底面,∴是三棱锥的高.
∵底面是矩形,∴.
∵点到平面的距离就是三棱锥的高,
∴由得:,
即,解得:,
即点到平面的距离为.
7.(23·24高二上·上海杨浦·期中)如图,为菱形外一点,平面,,为棱的中点.
(1)求证:平面;
(2)若,求到平面的距离.
【答案】(1)证明见解析
(2)
【详解】(1)连接,如图:
因为,四边形为菱形,
所以,
又为棱的中点,
所以,
因为,
所以,
因为平面,平面,
所以,
又平面,平面,
所以平面.
(2)因为平面,平面,
所以平面,
则到平面的距离即为点到平面的距离,
设点到平面的距离为,
因为,,平面,,四边形为菱形,
所以,
解得,
即到平面的距离为.
题型二:利用向量法求点到平面的距离
1.(23·24高二上·广东东莞·阶段练习)已知三棱柱的侧棱与底面垂直,,,M是的中点,N是的中点,P是的中点,则点A到平面的距离为( )
A.B.C.D.
【答案】D
【详解】解:如图,以A为原点,,,所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
则,,,
所以,,,
设平面的一个法向量,
则,令,则,,
所以平面的一个法向量,
所以,
即点A到平面的距离为.
故选:D.
2.(23·24高二上·广东佛山·阶段练习)如图,在四棱锥中,平面面,.
(1)证明:平面;
(2)求点到平面的距离.
【答案】(1)证明见解析
(2)
【详解】(1)取中点,连接,
由题意可知:,则∥,
且,则为为平行四边形,
由,所以四边形为矩形,
可知,则,
又因为,可知,即,
且平面平面,平面平面,平面,
所以平面.
(2)如图所示,以为原点,分别为轴、轴,过作垂直平面的直线,为轴,建立空间直角坐标系.
则,
可得,
设平面的法向量为,则,
令,则,可得,
所以到平面的距离为.
3.(23·24上·沧州·阶段练习)如图所示,四棱锥的底面是矩形,,,且底面,若边上存在异于的一点,使得直线.
(1)求的最大值;
(2)当取最大值时,求异面直线与所成角的余弦值;
(3)当取最大值时,求点到平面的距离.
【答案】(1)
(2)
(3)
【详解】(1)
建立如图空间直角坐标系,
设,则,,,,
则,.
因为,所以,即.
即,
当时,的最大值为.
(2)由(1)可知,当取最大值时,,,
所以.
所以异面直线与所成角的余弦值为.
(3)设平面的法向量为,则,,
因为,,,
所以,
取,则,,所以,
所以,
因为到平面的距离等于在上的射影长,
所以.
4.(23·24上·北辰·期中)如图,且且且平面.
(1)若为的中点,为的中点,求证:平面;
(2)求平面和平面夹角的正弦值;
(3)若点在线段上,且直线与平面所成的角为,求点到平面的距离.
【答案】(1)证明见解析;
(2);
(3).
【详解】(1)取GD中点为Q,连接NQ,MQ.
因为的中点,为的中点,Q为GD中点,
由三角形及梯形中位线定理,可得.
又注意到,平面EDC,平面EDC,
平面MNQ,,则平面平面.
又平面MQN,则平面.
(2)因平面ABCD,平面ABCD,
则,又,则如图建立以D为原点的空间坐标系.
则.
.
设平面和平面的法向量分别为.
则,取;
,取.
设平面和平面夹角为,则.
则平面和平面夹角的正弦值为.
(3)由(2),设,其中,则
又由题可得,平面的一个法向量可取.
结合直线与平面所成的角为,
则.
则,.
设平面法向量为,则.
取,则点到平面的距离.
5.(重庆市部分区2022-2023学年高二上学期期末联考数学试题)如图,在正方体中,.
(1)求证:;
(2)求点到平面的距离.
【答案】(1)证明见解析
(2)
【详解】(1)证明:以A为坐标原点,AD为x轴,AB为y轴,为z轴建立如图所示的坐标系.
∵,,,,
∴,,
∴,∴;
(2)∵,,∴,
设面的法向量为,
∵,,
∵,,∴,
令,则,,∴,
设到面的距离为d,
∴.
三、专项训练
一、单选题
1.(23·24高二上·陕西·阶段练习)如图,在正四棱柱中,,.点,,分别在棱,,上,,,,则点到平面的距离为( )
A.B.C.D.
【答案】D
【详解】以为坐标原点,,,所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
则,,,,,,.
设平面的法向量为,
则令,
得.
点到平面的距离为.
故选:D.
2.(23·24高二上·广东东莞·阶段练习)如图,在棱长为1的正方体中,为线段的中点,为线段的中点,则直线到平面的距离为( )
A.B.C.D.
【答案】D
【详解】由题意易知直线面,
所以到面的距离即为直线到平面的距离.
建立如图所示坐标系,则:
,,,,,
所以
设面的法向量,则:
,即
取,则,所以
所以到面的距离.
故选:D
3.(23·24高二上·湖南邵阳·阶段练习)在棱长为1的正方体中,分别是的中点,则直线到平面的距离为( )
A.B.C.D.
【答案】D
【详解】如图建立空间直角坐标系,则,,
所以,
设平面的法向量为,则
,令,则,
因为,平面,平面,
所以平面,所以直线到平面的距离即为点到平面的距离,
所以直线到平面的距离为 .
故选:D.
4.(23·24上·邯郸·阶段练习)在正三棱柱中,,点分别为棱的中点,则点到平面的距离为( )
A.B.C.D.
【答案】C
【详解】取的中点,以为坐标原点,所在直线分别为轴,轴,轴建立空间直角坐标系,
则,
所以,
设平面的一个法向量为,
所以令,解得,
所以平面的一个法向量为,
所以点到平面的距离.
故选:C.
5.(23·24上·绍兴·阶段练习)在棱长为1的正方体中,E为的中点,F为的三等分点靠近C点,则点E到平面BDF的距离为( )
A.B.C.D.
【答案】A
【详解】在棱长为1的正方体中,建立如图所示的空间直角坐标系,
则,,
设平面的法向量,则,令,得,
所以点到平面的距离为.
故选:A
6.(23·24高二上·北京·阶段练习)如图,在长方体中,,点B到平面的距离为( )
A.B.C.D.
【答案】C
【详解】
由题意得点到平面距离为三棱锥的高,
设点到平面距离为,取中点,连接,
因为为长方体,所以,所以,
,,,
所以,,解得.
故选:C.
7.(23·24高二上·湖南益阳·阶段练习)如图所示,在直三棱柱中,为棱的中点,则点到平面的距离是( )
A.B.C.D.
【答案】C
【详解】如图,连接,
因为三棱柱为直三棱柱,所以平面,
因为平面,所以,又因为,平面,
所以平面,所以点到平面的距离为,
因为,所以,,
因为为棱的中点,且平面,则易知,
则,则,
设点到平面的距离为,
则,即,
即,解得.
故选:C.
8.(23·24高二上·吉林长春·阶段练习)我国古代数学名著《九章算术》对立体几何问题有着深入的研究,从其中的一些数学用语可见.譬如“堑堵”指底面为直角三角形且侧棱垂直于底面的三棱柱,“阳马”指底面是矩形且有一侧棱垂直于底面的四棱锥,“鳖臑”指四个面都是直角三角形的三棱锥.现有一如图所示的“堑堵”,其中,若,则到平面的距离为( )
A.B.C.D.
【答案】B
【详解】
取中点,连结,
根据题意,平面,平面,
所以平面平面,
因为,所以,
又平面平面,平面
所以平面,且
由题意可知,
,
则,即为直角三角形,
,
设到平面的距离为,且,
即,
.
故选:B
9.(23·24高三上·河北沧州·阶段练习)在三棱柱中,平面,,,点D是的中点,点E是平面的中心,则点E到平面的距离为( )
A.B.C.D.
【答案】C
【详解】如图所示,连接,则点在上,再连接交于点,则为的中点,
因为为的中点,可得,
因为平面,平面,所以平面,
所以点到平面的距离等价于点到平面的距离,
设点到平面的距离为,由,即,
由,可得,
又由,,所以,
所以为直角三角形,所以,
所以,即点到平面的距离为.
故选:C.
二、填空题
10.(23·24高二上·宁夏固原·阶段练习)在棱长为1的正方体中,点到平面的距离为 .
【答案】/
【详解】如图所示,
设到平面的距离为h,
由得,
所以,
因为正方体的棱长为1,所以,,,
所以是等边三角形,
所以,
所以,即到平面的距离为.
故答案为:.
11.(23·24高二上·山西太原·阶段练习)如下图所示,在平行六面体中,各棱长均为2,已知,,则点A到平面的距离 .
【答案】/
【详解】取的中点,记为,连接,如下图:
在中,,,且为中点,所以,同理可得:,
由,则,且,
因为,平面,所以平面
在中,由余弦定理可得:,
由,,解得,
在中,,
所以,易知,
三棱锥的体积,
在中,由余弦定理可得:,
则,,
设到平面的距离为,.
故答案为:.
12.(23·24高二上·安徽·阶段练习)如图,四棱锥P-ABCD中,平面平面ABCD,底面ABCD是边长为2的正方形,是等边三角形,M,N分别为AB和PC的中点,则平面DMN上任意一点到底面ABCD中心距离的最小值为 .
【答案】
【详解】
连接相交于点,点为底面的中心,取中点为,连接,则,因为平面平面ABCD,则平面,
以点为原点,分别以为轴正半轴,建立如图所示空间直角坐标系,
且底面ABCD边长为2,是等边三角形,则,
,则,,则,
,设平面的法向量为,
则,解得,取,则,
,所以,且平面DMN上任意一点到底面ABCD中心距离的最小值即为点到平面的距离,则.
故答案为:.
13.(23·24高二上·天津西青·阶段练习)如图,棱长为2的正方体,点是棱的中点,点到直线的距离为 .
【答案】/
【详解】以为坐标原点,建立如图所示的空间直角坐标系,
因为正方体的棱长为2,所以,,,
所以直线方向向量 ,又 ,
,
所以在上的投影长为 ,
所以点到直线的距离为
故答案为:.
三、解答题
14.(23·24高三上·四川成都·阶段练习)已知正方形的边长为2,为等边三角形(如图1所示).沿着折起,点折起到点的位置,使得侧面底面.是棱的中点(如图2所示).
(1)求证:;
(2)求点与平面的距离.
【答案】(1)见解析
(2)
【详解】(1)如图,取AB中点O,连接交于,
∵为等边三角形,
∴,
又∵平面平面,平面,平面平面,
故平面,
而平面,∴,
又∵,,
∴.
∴,
又∵平面,平面,,
∴平面,
∵平面,
∴.
(2)设点与平面的距离为,
∵ABCD是正方形,△PAB为等边三角形,
∴,,
又∵平面平面,平面,平面平面,
故⊥平面,
而平面,所以,,
∴在中,,
∴,则易得,
由(1)知,平面,
∴为三棱锥的高,
∴
又∵,
得.
故点与平面的距离为.
15.(23·24高二上·广东东莞·阶段练习)如图,已知一个组合体由一个圆锥与一个圆柱构成(圆锥底面与圆柱上底面重合.平面为圆柱的轴截面),已知圆锥高为3,圆柱高为5,底面直径为8.
(1)求这个组合体的体积
(2)设为半圆弧的中点,求到面的距离.
【答案】(1);
(2).
【详解】(1)依题意,圆锥的底面圆半径为4,而其高为3,则圆锥的体积,
圆柱的底面圆半径为4,高为5,则圆柱的体积,
所以这个组合体的体积为.
(2)连接,由为半圆弧的中点,得,,
而平面,平面,则,,平面,
于是平面,显然圆锥与圆柱有共同的旋转轴,即点在平面内,
因此三棱锥的高为,且,
设到平面的距离为,由,得,
即,从而,
故到平面的距离为.
16.(23·24高三上·广东佛山·阶段练习)如图,在正三棱柱中,点为侧棱的中点,且.
(1)证明:平面平面
(2)若二面角的大小为,求点到平面的距离.
【答案】(1)证明见解析;
(2)
【详解】(1)法一:
取中点的中点,连接与,
则,且
又为中点,,且,
四边形是平行四边形,.
在正三棱柱中,平面平面,
,又为等边三角形,,
又平面,
平面,又平面,
平面平面,
法二如图,以原点,垂直于的直线为轴,建立空间直角坐标系,
设,则,
,
设平面的一个法向量为,则
,
取,则
又平面的法向量为,
,
平面平面
(2)方法一:取中点,连接,
,
在正三棱柱中,,
是二面角的平面角,
又平面,
设点到平面的距离为,则,
,即点到平面的距离为.
方法二:由(1)得,
设平面的一个法向量为,则
,
,取,则
又平面的法向量为,
二面角的大小为
,
由于,
,又,
点到平面的距离为.
17.(23·24高二上·辽宁·阶段练习)如图,六面体中,面且面,,,.
(1)求证:平面;
(2)若二面角的余弦值为,求点到直线的距离.
【答案】(1)证明见解析
(2)
【详解】(1)证明:因为面且面,
面且面,
所以且,
在面中,,
同理,在面中,,
因为,
所以,
又,
所以,
所以,
所以,
由面,面,知,
又因为,面,面,
所以面.
(2)取中点,由题可知,且,
所以四边形为平行四边形,所以,
因为面,故面,
又因为为正三角形,所以,,两两垂直,
以为坐标原点,以的方向分别为,,轴正方向,建立如图所示的空间直角坐标系,
设,则,,,
,,,,
设面的法向量为,则有,
不妨设,得,
又面,故面的法向量不妨设为,
由题意,解得,
于是,,,
所以点到到直线的距离为.
18.(23·24高二上·北京通州·期中)如图,在正方体中,分别是棱,,,的中点.
(1)求证:四点共面;
(2)求与平面所成角的正弦值;
(3)求点到平面的距离.
【答案】(1)证明见详解
(2)
(3)
【详解】(1)如图,取的中点 连接,
因为分别是棱,,,的中点,
易得,,所以,
所以四点共面,
又,
所以,
则四点共面,
而过不共线的的三点的平面具有唯一性,
则平面与平面重合,
故四点共面.
(2)以为原点,所在直线分别为轴、轴、轴,
建立如图所示的空间直角坐标系,
设正方形的的边长为
则
则,
设是平面的法向量,
则,
取,则所以,
所以与平面所成角的正弦值为
(3)由(2)知平面的法向量,
又
所以点到平面的距离为
,
即到平面的距离为
相关试卷
这是一份【专项复习】高考数学专题03 正态分布 (题型训练).zip,文件包含专项复习高考数学专题03正态分布题型训练原卷版docx、专项复习高考数学专题03正态分布题型训练解析版docx等2份试卷配套教学资源,其中试卷共55页, 欢迎下载使用。
这是一份【专项复习】高考数学专题04 数列求通项(隔项等差(等比)数列)(题型训练).zip,文件包含专项复习高考数学专题04数列求通项隔项等差等比数列题型训练原卷版docx、专项复习高考数学专题04数列求通项隔项等差等比数列题型训练解析版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
这是一份【专项复习】高考数学专题04 圆锥曲线中的定点、定值、定直线问题(题型训练).zip,文件包含专项复习高考数学专题04圆锥曲线中的定点定值定直线问题题型训练原卷版docx、专项复习高考数学专题04圆锥曲线中的定点定值定直线问题题型训练解析版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。









