【专题复习】高考数学 专题14 三次函数.zip

这是一份【专题复习】高考数学 专题14 三次函数.zip，文件包含专题复习高考数学专题14三次函数原卷版docx、专题复习高考数学专题14三次函数解析版docx等2份试卷配套教学资源，其中试卷共55页， 欢迎下载使用。
函数与导数一直是高考中的热点与难点, 我们知道二次函数是重要的且具有广泛应用的基本初等函数,学生对此已有较为全面、系统、深刻的认识,并在某些方面具备了把握规律的能力,由于三次函数的导数是二次函数,使得我们可以利用二次函数研究三次函数的图象与性质,这使得三次函数成为高考数学的一个热点.
二、解题秘籍
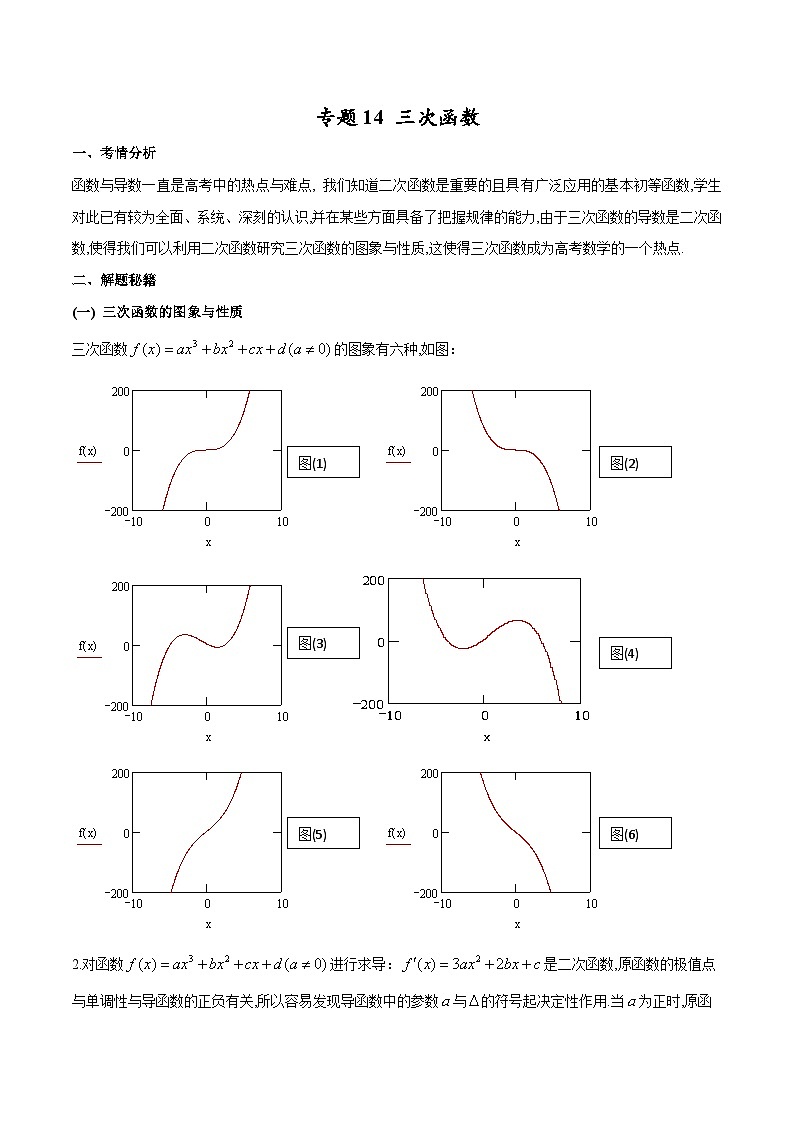
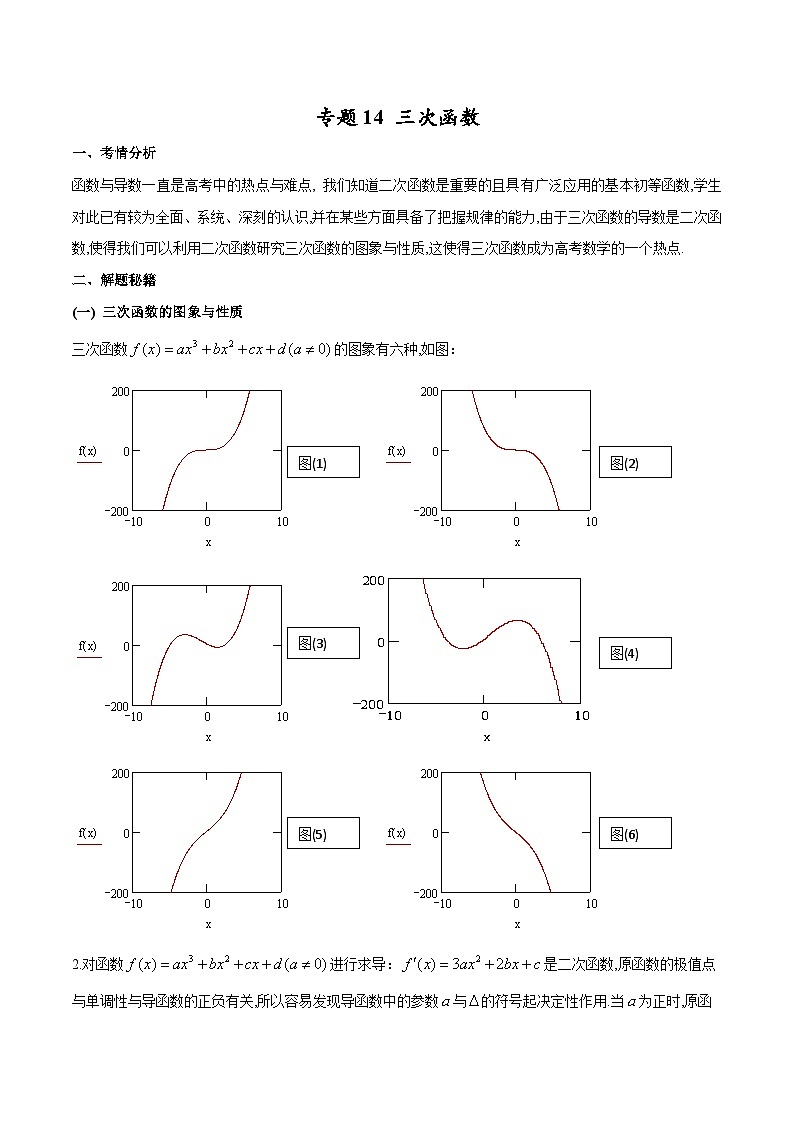
(一) 三次函数的图象与性质
三次函数的图象有六种,如图：
图(2)
图(1)

图(4)
图(3)

图(5)
图(6)
2.对函数进行求导：是二次函数,原函数的极值点与单调性与导函数的正负有关,所以容易发现导函数中的参数与的符号起决定性作用.当为正时,原函数的图象应为上图中的（1）、（3）、（5）三种情况；而当为负时,原函数的图象则为（2）、（4）、（6）三种情况.当时,二次方程有两相异实根,且在的两边的符号相反,故函数存在两个极值点,图象为上图中的（3）、（4）两种；当时,二次方程有两相等实根,且在根的两边的符号相同,这时函数只存在驻点（但不是极值点）,函数的图象为上图中（1）、（2）两种,当时；方程无实根,的值恒为正（或负）,函数的图象为上图中的（5）、（6）两种.
仔细观察图象,我们还不难发现三次函数是中心对称曲线,这一点可以得到进一步的验证:设,得
整理得,.据多项式恒等对应系数相等,可得且,从而三次函数是中心对称曲线,且由知其对称中心仍然在曲线上.而是否具有特殊的意义？对函数进行两次求导,再令等于0,得,恰好是对称中心的横坐标,这可不是巧合,因为满足的正是函数拐点的横坐标,这一性质刚好与图象吻合.除此,三次函数的对称中心还有一个很少引起注意的性质---过三次曲线的对称中心且与该三次曲线相切的直线有且仅有一条；而过三次曲线上除对称中心外的任一点与该三次曲线相切的直线有二条.由于三次曲线都是中心对称曲线,因此,将其对称中心移至坐标原点便可将三次函数的解析式简化为.
若M（x1,y1）是三次曲线上的任一点,设过M的切线与曲线y=f（x）相切于（x0,y0）,则切线方程为,因点M上此切线上,故,又,所以,整理得：,解得,或.
综上所述,当点M是对称中心即时,过点M作曲线的切线切点是惟一的,且为M,故只有一条切线；当点M不是对称中心即时,过点M作曲线的切线可产生两个不同的切点,故必有两条切线,其中一条就是以M为切点（亦即曲线在点M处）的切线.
由此可见,不仅切线与曲线的公共点可以多于一个,而且过曲线上点的切线也不一定惟一求以曲线上的点(x0,f(x0))为切点的切线方程的求解步骤：①求出函数f(x)的导数f′(x)；②求切线的斜率f′(x0)；③写出切线方程y－f(x0)＝f′(x0)(x－x0),并化简．
【例1】（2023届黑龙江省哈尔滨市高三上学期12月月考）设函数
(1)若，，求曲线在点处的切线方程；
(2)若，不等式对任意恒成立，求整数k的最大值．
【解析】（1）当，时，，所以，即切点为
因为，所以，
所以切线方程为，即，
（2），由，所以，
所以函数在R上单调递增
不等式，对恒成立，
构造，，
构造，，对有，
所以在递增，，，
所以，，
所以，，即，在递减，
，，即，在递增，
所以，结合，故，
所以对恒成立，故，
所以整数k的最大值为3；
(二)三次函数的零点
1.若三次函数没有极值点,则有1个零点；
2. 三次函数有2个极值点,则时有1个零点；时有2个零点；时有3个零点.
【例2】（2023届江西省赣抚吉十一校高三第一次联考）已知函数,其中.
(1)若的极小值为－16,求；
(2)讨论的零点个数.
【解析】（1）由题得,其中,当时,,单调递增,无极值；当时,令,解得或；令,解得,所以的单调递减区间为,单调递增区间为,,所以当时,取得极小值,所以,解得.
（2）由（1）知当时,的极小值为,的极大值为, 当,即时,有三个零点,如图①曲线 ；当,即时,有两个零点,如图②曲线；当,即时,有一个零点,如图③曲线；当时,,易知有一个零点. 综上,当时,有一个零点；当时,有两个零点；当时,有三个零点.
(三)过平面上一点P作三次函数图象的切线的条数
此类问题一般是先设出切点Q,写出曲线在处的切线方程,把点P坐标代入,整理出一个关于t的三次方程,该方程实根个数就是切线条数.
【例3】（2024届江苏省南通市高三上学期期初质量监测）已知函数的极小值为，其导函数的图象经过，两点.
(1)求的解析式；
(2)若曲线恰有三条过点的切线，求实数的取值范围.
【解析】（1），
因为，且的图象经过，两点.
所以当时，，单调递增；
当时，，单调递减；
当时，，单调递增.
所以在处取得极小值，所以，
又因为，，所以，，
解方程组得，，，
所以.
（2）设切点为，则，
因为，所以，
所以切线方程为，
将代入上式，得.
因为曲线恰有三条过点的切线，所以方程有三个不同实数解.
记，则导函数，
令，得或1.
列表：
所以的极大值为，的极小值为，
所以，解得.故的取值范围是.
(四)含参数的三次函数的单调性的讨论
求含参数的三次函数在闭区间上的最值,一般根据函数极值点与闭区间的位置关系进行讨论.
【例4】（2024届内蒙古包头市高三上学期调研）已知函数．
(1)讨论的单调性；
(2)若有2个零点，求的值．
（注：）
【解析】（1），，
当，即时，，所以在上单调递增，
当，即或时，
令，解得，，
当时，，
当时，，
当时，，
所以在上单调递增，在上单调递减，
综上所述，当时，在上单调递增，
当或时，在上单调递增，在上单调递减；
（2）当时，，此时函数无零点，
当时，等价于，
设，，则，
当时，，故单调递增，且，
当时，，故单调递减，
当时，，故单调递增，
又，当且时，，当时，，
如图作出函数的大致图象，

由图可知，要使，两个函数有两个交点，则，
即当时，有且只有2个零点．
(五)三次函数与韦达定理的交汇
由于三次函数的导数是二次函数,而二次函数常与韦达定理交汇,故有时可以用定理交汇处理三次函数问题
【例5】设是函数的两个极值点,且
(1)求a的取值范围；
(2)求证：.
【解析】(1),的两个实根,又a＞0
,
由得
(2)设则
上单调递增
,
三、典例展示
【例1】（2024届海南省琼中县高三上学期9月全真模拟）已知函数，．
(1)当时，求在上的值域；
(2)若的极小值为，求m的值．
【解析】（1）当时，，则，
令，得或，
当x变化时，，的变化情况如表所示：
所以在上的值域为．
（2）由，得，
令，得或，
因为，
令，得；
令，得或，
所以在和上单调递增，在上单调递减，
在处取得极小值，
令，
解得，故m的值为6．
【例2】（2024届贵州省贵阳第一中学高三上学期适应性月考）已知函数.
(1)求函数在处的切线方程；
(2)若过点存在3条直线与曲线相切，求的取值范围；
(3)请问过点，，，，分别存在几条直线与曲线相切？（请直接写出结论，不需要证明）
【解析】（1）因为，所以.
又，
根据导数的几何意义可知，函数在处的切线的斜率为，
所以，切线方程为.
（2）设切点为，则，
切线方程为，
整理可得，.
又点在切线上，则.
要使过点存在3条直线与曲线相切，则该方程有个解.
令，则.
解，可得，所以在上单调递增；
解，可得或，所以在上单调递减，在上单调递减.
所以，在处取得极小值，在处取得极大值.
又，，由题意可知，.
（3）设切点为，则，
切线方程为.
①当点在切线上时，有，此时，即点为切点.
由（1）知，切线为1条；
②当点在切线上时，
由（2）知，在处取得极小值，且，
所以，此时，只有1个解，即只存在1条切线；
③当在切线上时，
由（2）知，，解得或.
所以此时存在2条切线；
④设切线过
此时有.
令，则.
解，可得，所以在上单调递增；
解，可得或，所以在上单调递减，在上单调递减.
所以，在处取得极小值，在处取得极大值.
又，，
所以，当时，有3条切线.
所以，过点的切线有3条.
又方程，可化为，
解得或，
所以，过点的切线有2条.
【例3】（2023届江苏省徐州市睢宁县高三下学期5月模拟）已知函数，，且在上的极大值为1．
(1)求实数的值；
(2)若，，，求的值．
【解析】（1），，
① 时，，∴，无极值．
② 时，，∴，
当，即时，，无极大值；
当时，时，；时，，
∴在处取极大值，即，∴，舍去．
③时，，
∴，
时，；时，；时，．
∴在处取极大值，∴符合题意．
综上，．
（2）由（1）可知，，，
令可得，令可得或，
如图所示．

① 当时，，
当时，，则，矛盾；
当时，，∴，矛盾．
② 当时，符合题意．
③ 当时，时，，∴，
则，，∴，矛盾．
④ 当时，符合题意．
⑤ 当时，时，，∴，
则，，∴，矛盾．
⑥ 当时，符合题意．
⑦ 当时，，则，∴，与矛盾．
⑧ 当时，，，∴，与矛盾．
综上，，或，或．
【例4】（2023届重庆市第十一中学校高三上学期11月质量检测）已知函数，在处取极大值，在处取极小值.
(1)若，求函数的单调区间；
(2)在方程的解中，较大的一个记为，在方程的解中，较小的一个记为，证明：为定值.
【解析】（1）当时，，定义域为R，，
当时，或；当时，；
即函数的单调增区间为，；单调减区间为.
（2）由，
根据题意，得的两根为，且，
即，得，
，
所以，
因为，则，
可知，
因为，即，
即，
可知，同理，由，
可知；
得到，
所以.
【例5】（2023届上海市嘉定区高三三模）已知函数，其导函数为，
(1)若函数有三个零点，且，试比较与的大小.
(2)若，试判断在区间上是否存在极值点，并说明理由.
(3)在（1）的条件下，对任意的，总存在使得成立，求实数的最大值.
【解析】（1）因为，故一正一负，
，所以，所以是方程的两根，
由韦达定理得，
因为
所以，故，，，
因为，，所以；
（2），开口向上，
，，，
①当时，，
根据零点存在定理可知，存在使得，
且时，，单调递增，时，，单调递减，
所以在区间上存在极大值点，
②当时，，，
根据零点存在定理可知，存在使得，且时，，
时，，所以在区间上存在极小值点；
（3）对任意的，总存在使得成立，
设，的最大值为，则，
即①，②，③，
由①+③得④，
由②得⑤，
④+⑤得，即，
当且仅当，即时取等，所以的最大值为2.
【例6】设函数,其中,为常数．
(1)讨论的单调性；
(2)若函数有且仅有3个零点,求的取值范围．
【解析】 (1)．
当时,,或,,,
当时,,或,,,
当时,,
综上,当时,在,上单调递增,上单调递减；
当时,在和上单调递增,上单调递减；
当时,在上单调递增．
(2)由（1）可知,有3个零点,
则且,
∴,
∴．
四、跟踪检测
1.（2024届江苏省镇江市丹阳市高三上学期期初检测）已知函数在处有极小值.
(1)求m的值；
(2)求函数在上的最大值.
2.（2023河南省新未来3月联考）已知函数．
(1)若，求函数的极值；
(2)当时，若对，恒成立，求的最小值．
3．（2023届安徽省卓越县中联盟高三上学期第一次联考）已知函数，．
(1)若在上的值域为，求在上的单调区间；
(2)若函数，则当时，求的零点个数．
4．（2023届湖南省湘潭市部分学校高三上学期期末联考）已知函数，其中．
(1)当时，求函数的单调区间；
(2)已知函数(是自然对数的底数)，若，曲线与曲线都有唯一的公共点，求实数m的取值范围．
5．（2023届北京市第五中学高三下学期3月检测）设函数，
(1)当时，求函数的单调增区间；
(2)若函数在区间上为减函数，求的取值范围；
(3)若函数在区间内存在两个极值点，，且，求的取值范围.
6．已知函数（）有极值，且导函数的极值点是的零点．
(1)求关于的函数关系式，并写出定义域；
(2)求证：；
(3)若这两个函数的所有极值之和不小于，求的取值范围．
7．已知.
(1)当时，求函数的单调减区间；
(2)当时，曲线在相异的两点点处的切线分别为和和的交点位于直线上，证明：两点的横坐标之和小于4.
8．（2024届江西省稳派上进教育高三上学期摸底考试）已知函数，，，分别为，的导函数，且对任意的，存在，使．
(1)求实数a的取值范围；
(2)证明：，有．
9.已知函数,,,
（1）若函数在区间上不单调,求的取值范围；
（2）求的最大值；
（3）若对任意恒成立,求的取值范围．
10.已知函数在处的切线与轴平行．
（1）求的值和函数的单调区间；
（2）若函数的图象与抛物线恰有三个不同交点,求的取值范围．
11.已知函数
（1）（i）求函数的图象的交点A的坐标；
（ii）设函数的图象在交点A处的切线分别为是否存在这样的实数a,
使得？若存在,请求出a的值和相应的点A坐标；若不存在,请说明理由.
（2）记上最小值为F（a）,求的最小值.
12.已知函数在时有极小值.
(1)当时,求在处的切线方程；
(2)求在上的最小值.
13.已知函数,其中．
(1)求函数的单调区间；
(2)设函数在区间上的最大值为,证明：．
14.已知函数,其中.
（1）求曲线在点处的切线方程；
（2）若存在实数,使得不等式的解集为,求的取值范围.
15.已知函数．
(1)讨论函数的单调性；
(2)若函数在区间上的最大值与最小值之差为,求的最小值．
16.已知函数在上的最小值为．
（1）求a的值；
（2）讨论函数的零点个数．0
1
+
0
-
0
+
↗
极大
↘
极小
↗
x
0
1
＋
0
－
0
＋
单调递增
极大值0
单调递减
极小值
单调递增
0