山西省运城市多校2023-2024学年七年级下学期期中数学试题（原卷版+解析版）

这是一份山西省运城市多校2023-2024学年七年级下学期期中数学试题（原卷版+解析版），文件包含山西省运城市多校2023-2024学年七年级下学期期中数学试题原卷版docx、山西省运城市多校2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
注意事项：
1．本试卷分第Ⅰ卷和第Ⅱ卷两部分．全卷共6页，满分120分，考试时间120分钟．
2．答卷前，考生务必将自己的姓名、准考证号填写在本试卷相应的位置．
3．答案全部在答题卡上完成，答在本试卷上无效．
4．考试结束后，将本试卷和答题卡一并交回．
第Ⅰ卷 选择题（共30分）
一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该选项涂黑）
1. 计算的结果为（ ）
A. B. C. D. 2
【答案】C
【解析】
【分析】根据负整数指数幂的意义即可求解．
【详解】解：．
故选：C．
【点睛】本题考查了负整数指数幂的意义，掌握（，为正整数）是解题的关键．
2. 如图，三角板的直角顶点恰好在直尺的边上．若，则的度数为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查了平行线的性质，根据得，再根据平角的定义即可求解，熟知两直线平行，同位角相等是解题的关键．
【详解】解：∵，
∴，
∵，，
∴，
故选：．
3. 下列运算结果正确的是（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】本题考查了同底数幂的乘法（除法），幂的乘方，平方差公式，解题的关键是掌握同底数幂相乘（除），底数不变，指数相加（减）；幂的乘方，底数不变，指数相乘；平方差公式．据此逐个判断即可．
【详解】解：A、，故A不正确，不符合题意；
B、，故B正确，符合题意；
C、，故C不正确，不符合题意；
D、，故D不正确，不符合题意；
故选：B．
4. 下列各选项能用“直线外一点与直线上各点连接的所有线段中，垂线段最短”来解释的现象是（ ）
A. 测量跳远成绩B. 木板上弹墨线
C. 两钉子固定木条D. 弯曲河道改直
【答案】A
【解析】
【分析】根据垂线段最短、两点确定一条直线和两点之间、线段最短逐项判断即得答案
本题考查了垂线段最短、两点确定一条直线和两点之间线段最短等知识，属于应知应会题型，熟知以上基本知识是解题的关键
【详解】解：A、测量跳远成绩可以用“垂线段最短”来解释，故本选项符合题意；
B、木板上弹墨线可以用“两点确定一条直线”来解释，故本选项不符合题意；
C、两钉子固定木条可以用“两点确定一条直线”来解释，故本选项不符合题意；
D、弯曲河道改直可以用“两点之间，线段最短”来解释，故本选项不符合题意；
故选：A
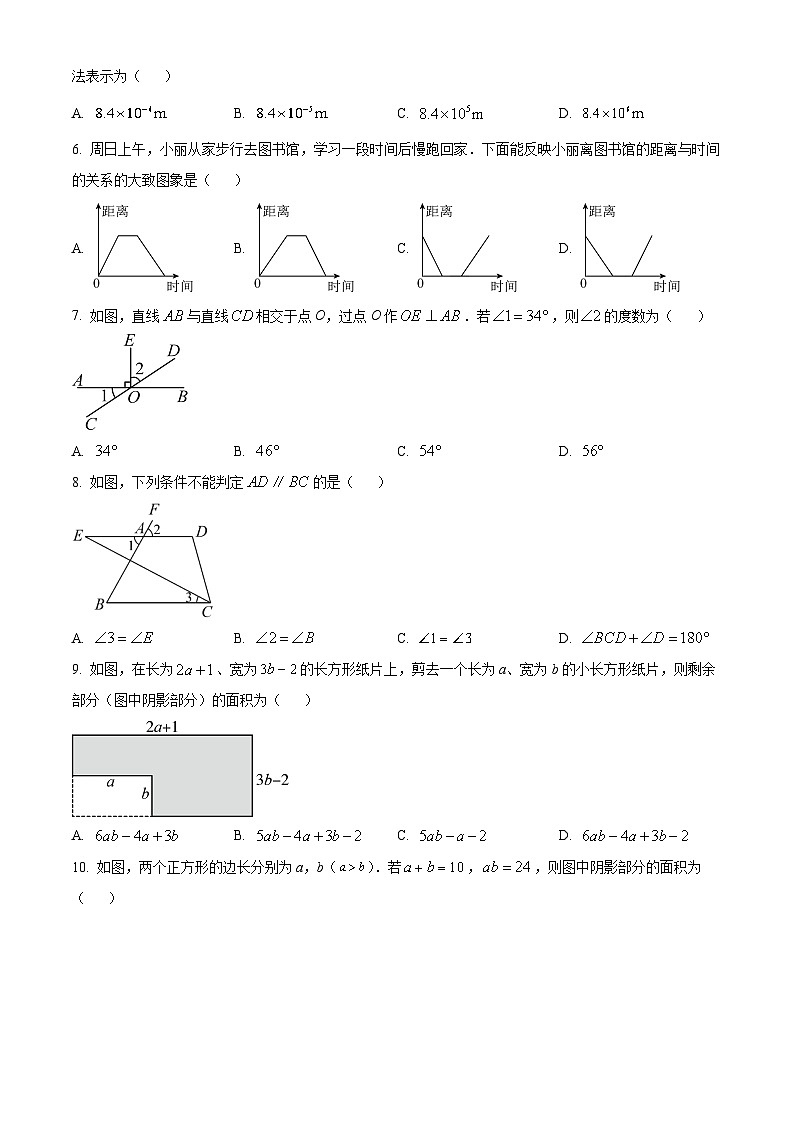
5. 清代诗人袁枚的一首诗《苔》：“白日不到处，青春恰自来．苔花如米小，也学牡丹开．”歌颂了苔在恶劣环境下仍有自己的生命意向．若苔花的花粉直径约为0.0000084m，则数据“0.0000084m”用科学记数法表示为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】此题考查了科学记数法的表示方法：将一个数写成的形成，，n是整数，当原数绝对值小于1时，n是负整数，n等于原数左数第一个非零数前面0的个数的相反数，据此解答．
【详解】解：，
故选：A．
6. 周日上午，小丽从家步行去图书馆，学习一段时间后慢跑回家．下面能反映小丽离图书馆的距离与时间的关系的大致图象是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了函数的图象与实际生活的联系，根据在每段中，离图书馆的距离随时间的变化情况即可进行判断．
【详解】解：图象应分三个阶段，
第一阶段：跑步到图书馆，在这个阶段，离图书馆的距离随时间的增大而减小；
第二阶段：在图书馆学习一会，这一阶段图书馆的距离不随时间的变化而改变，即为0；
第三阶段：慢跑回家，这一阶段，离图书馆的距离随时间的增大而增大，并且这段的速度大于第一阶段的速度．
故选：D．
7. 如图，直线与直线相交于点O，过点O作．若，则的度数为（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了两条相交线所成的角，垂直的定义，平角的定义．由已知可得，，进而根据，，即可求得．
【详解】解：，
，
，，
．
故选：D．
8. 如图，下列条件不能判定的是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了平行线的判定，根据平行线的判定定理即可求解，掌握平行线的判定定理是解题的关键．
【详解】解：A、∵，∴，即，故选项不符合题意；
B、∵，∴，故选项不符合题意；
C、，不能判定，故选项符合题意；
D、∵，∴，故选项不符合题意；
故选：C．
9. 如图，在长为、宽为的长方形纸片上，剪去一个长为a、宽为b的小长方形纸片，则剩余部分（图中阴影部分）的面积为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了多项式乘以多项式，熟练掌握多项式乘法以及单项式乘以多项式的运算法则是解本题的关键．
根据图形可知阴影部分面积等于长为米，宽为米的长方形面积减去长为a米，宽为b米的长方形面积，然后根据整式的混合运算法则进行化简即可；
【详解】解：根据题意可得：
阴影部分面积
，
故选：B．
10. 如图，两个正方形的边长分别为a，b（）．若，，则图中阴影部分的面积为（ ）
A. 20B. 18C. 16D. 14
【答案】D
【解析】
【分析】本题考查了完全平方公式的变形求值，掌握求解的方法、熟练进行完全平方公式的变形是解题关键；
根据阴影部分的面积=两个正方形的面积和-两个直角三角形的面积结合完全平方公式变形求解即可
【详解】解：∵，，
∴阴影部分的面积
；
故选：D.
第Ⅱ卷 非选择题（共90分）
二、填空题（本大题共5个小题，每小题3分，共15分．请将答案直接写在答题卡相应的位置）
11. 计算的结果为______
【答案】1
【解析】
【分析】此题考查了零指数计算，任意非零数的零次幂都等于1，据此解答.
【详解】解：，
故答案：1.
12. 若一个角和它的余角相等，则这个角的度数为______
【答案】##45度
【解析】
【分析】本题考查了余角的概念，找出关系列方程是解题关键．
设这个角度为x，表示余角，根据等量关系列方程，解方程即可．
【详解】解：设这个角度为
由题意得：
解得：
故答案为：
13. 计算的结果为______
【答案】##
【解析】
【分析】本题主要考查了有理数的乘方运算等知识点，先根据乘方意义，把写成的形式，然后利用积的乘方法则进行简便计算即可，解题关键是熟练掌握逆用积的乘方法则进行简便计算．
【详解】
，
故答案为：．
14. 如图，，平分．若，则的度数为______
【答案】
【解析】
【分析】本题考查了平行线的判定与性质，角平分线的定义，解题的关键是掌握两直线平行，同位角相等，内错角相等，同旁内角互补．
根据推出，则，根据角平分线的定义，得出，最后根据两直线平行，同旁内角互补，即可解答．
【详解】解：∵，
∴，
∵，
∴，
∵平分，
∴，
∴，
故答案为：．
15. 如图，在梯形中，，动点从点出发，沿匀速运动．点运动的路程与三角形的面积变化情况如图所示，则梯形的面积为_____．
【答案】
【解析】
【分析】本题考查了动点问题的函数图象，根据图象可得出的长，当面积为时即可求出，再根据图象可得的长，弄清函数图象上的信息是解题的关键．
【详解】解：根据图象可知，，
当面积时，，
∴，
∴梯形的面积为，
故答案为：．
三、解答题（本大题共8个小题，共75分．解答应写出文字说明、推理过程或演算步骤）
16. 计算：
（1）；
（2）．
【答案】（1）
（2）
【解析】
【分析】本题主要考查了整式的混合运算等知识点，
（1）直接利用乘法公式和整式的乘法法则化简，进而合并同类项得出答案；
（2）利用多项式除以单项式的运算法则进行运算即可；
准确熟练地进行计算是解题的关键．
【小问1详解】
；
【小问2详解】
．
17. 先化简，再求值，其中，．
【答案】，
【解析】
【分析】先去括号，再合并同类项，然后把，代入化简后的结果，即可求解．
【详解】解：原式
．
当，时，原式．
18. 如图，在一张地图上有A，B，C三个城市，其中城市C的位置被墨迹污染了，但知道，，请你在图中确定城市C的具体位置．（要求：尺规作图，保留作图痕迹，标明字母，不写作法）

【答案】见解析
【解析】
【分析】本题考查作图−作一个角等于已知角，解题的关键是熟练掌握五种基本作图，属于中考常考题型．如图作，射线交射线于点C，点C即为所求．
【详解】解：如图作，射线交射线于点C，
点C即为所求．

19. 如图，已知，，试说明．
在下列解答过程中填写理由，
解：因为，
所以（____________）
所以（____________）
又因为，
所以．
所以（____________）．
所以（____________）．
【答案】同旁内角互补，两直线平行；两直线平行，同位角相等；内错角相等，两直线平行；两直线平行，同旁内角互补
【解析】
【分析】此题考查了平行线的性质和判定，根据平行线的判定定理和性质定理分析解答，熟练掌握平行线的性质和判定定理是解题的关键．
【详解】解：因为，
所以（同旁内角互补，两直线平行）
所以（两直线平行，同位角相等）
又因为，
所以．
所以（内错角相等，两直线平行）．
所以（两直线平行，同旁内角互补）．
20. 为保持水质洁净，某游泳馆为游泳池定期换水．已知该游泳池换水前已存水，换水时关闭进水孔、打开排水孔，以每小时的速度放水，游泳池的存水量与放水时间的变化情况如下表：
（1）在这个变化过程中，自变量是______，因变量是______．
（2）请你估计当放水时间为时，游泳池的存水量为______．
（3）设放水时间为，游泳池的存水量为，请你直接写出y与x的关系式．（不要求写出自变量的取值范围）
（4）根据表格中的数据，请你写出在一定范围内，游泳池的存水量与放水时间的变化情况．
【答案】（1）放水时间，游泳池的存水量
（2）152 （3）
（4）见解析
【解析】
【分析】本题考查了函数的基础知识：变量，求函数关系式等知识；
（1）根据自变量和因变量的定义，即可解答；
（2）根据排水孔以每小时78立方米的速度放水，列出算式进行计算即可；
（3）根据存水量=原有水量放出水量，即可得出函数解析式；
（4）根据表中数据进行分析即可．
【小问1详解】
解：根据题意可得：在这个变化过程中，自变量是放水时间，因变量是游泳池的存水量，
故答案为：放水时间，游泳池的存水量；
【小问2详解】
解：当放水时间为时，游泳池的存水量为，
故答案为：152；
【小问3详解】
解：∵换水前存水量为912立方米，每小时放水76立方米，
∴；
【小问4详解】
解：一定范围内，放水时间每增加，游泳池的存水量减少．
21. 如图，将某手机后视摄像头抽象成数学图形，其主体是一个圆环，大圆的半径为r，与大圆同心的空白小圆的半径为，在圆环中有三个半径为的小圆，有一个由两个直径为的半圆和一个长为的长方形组成的平面图形．
（1）求阴影部分的面积（用含r和a的代数式表示）
（2）当，时，计算阴影部分的面积（取3）
【答案】（1）
（2）
【解析】
【分析】本题考查了列代数式表达式以及已知字母的值求代数式的值，正确掌握相关性质内容是解题的关键．
（1）运用阴影面积等于大圆面积分别减去空白面积，列式代数计算化简得，即可作答．
（2）再把，分别代入，即可作答．
【小问1详解】
解：阴影部分的面积为
．
答：阴影部分的面积为．
【小问2详解】
解：当，时，
原式．
答：阴影部分的面积为．
22. 甲、乙两人从学校出发，沿一条笔直的路向同一方向行驶，如图表示甲步行、乙骑自行车所走的路程与时间的关系．观察图象并回答下列问题：
（1）乙出发时，与甲相距______．
（2）走了一段路程后，乙的自行车发生故障，停下来修车，则修车的时间为______h．
（3）乙从出发起，经过______h追上甲．
（4）乙骑自行车发生故障前的速度与修车后的速度一样吗？为什么？
【答案】（1）8 （2）1.5
（3）3.5 （4）不一样，理由见详解
【解析】
【分析】本题考查一次函数的应用、路程、速度、时间的关系等知识，解题的关键是灵活运用图中信息解决问题．
（1）根据时甲乙两人的路程差即为两人的距离解答；
（2）根据路程不变的时间即为修车时间解答；
（3）根据两人的函数图象的交点即为相遇写出时间即可；
（4）根据“速度＝路程÷时间”解答即可．
【小问1详解】
解：由图象可知：乙出发时，与甲相距，
故答案为：10．
【小问2详解】
解：由图象可知：修车时间为，
故答案为1.5．
小问3详解】
解：由图象可知：乙从出发起，经过追上甲，
故答案为：3.5．
【小问4详解】
解：发生故障前的速度为千米/小时，修车后的速度为：千米/小时，因此速度不一样．
23. 综合与实践
问题情境：
“综合与实践”课上，老师提出如下问题：如图1，已知直线，在三角板中，，，将其顶点A放在直线上，并使直线于点D，与直线交于点E．试说明直线．
（1）请解答老师提出的问题．
操作探究：
（2）如图2，将图1中的三角板的顶点A放在两平行线之间，AB与直线交于点M，得到，AC与直线交于点N，得到．
试探究与的数量关系，并说明理由．
下面是小明同学不完整的解答过程，请你补充完整．
解：．理由如下：
如图5，过点A作直线，则______．
因为直线，
所以直线（____________）．
所以______（____________）．
因______，，
所以．
深入探究：
（3）如图3，在图2的基础上，F为两平行线之间一点，连接，使他们分别平分和的对顶角，请直接写出的度数．
（4）如图4，在图2的基础上，G为两平行线之间一点，连接，使平分的对顶角，．若，请直接写出的度数．
【答案】（1）见解析（2）见解析；（3）；（4）
【解析】
【分析】题目主要考查利用平行线的判定和性质求角度，熟练掌握平行线的判定和性质，作出辅助线是解题关键．
（1）根据垂直定义得出，再由平行线的判定即可证明；
（2）根据题干中给出的证明过程，结合图形即可证明；
（3）过先F作，根据平行线性质及角平分线的计算求解即可；
（4）过先G作，根据平行线的性质及角平分线的计算求解即可．
【详解】解：（1）直线于点D，
∴，
∵，
∴，
∴直线；
（2）过点A作直线，则．
因为直线，
所以直线（平行于同一条直线的两条直线平行）．
所以（两直线平行，同位角相等）．
因为，，
所以；
故答案为：；平行于同一条直线的两条直线平行；；两直线平行，同位角相等；；
（3）过先F作，如图所示：
∴，
∴，
∵分别平分和的对顶角，
∴，
由（2）得，
∴；
（4）过点G作，如图所示：
∴，
∴，
∵平分对顶角，，
∴，，
由（2）得，
∴，
∴．游泳池的存水量/
836
760
684
608
532
456
放水时间/
1
2
3
4
5
6