




【二轮复习】高考数学专题15 立体几何解答题全归类(考点专练)(原卷版+解析版)
展开
这是一份【二轮复习】高考数学专题15 立体几何解答题全归类(考点专练)(原卷版+解析版),文件包含二轮复习高考数学专题15立体几何解答题全归类考点专练原卷版docx、二轮复习高考数学专题15立体几何解答题全归类考点专练解析版docx等2份试卷配套教学资源,其中试卷共99页, 欢迎下载使用。
目 录
TOC \ "1-3" \h \z \u \l "_Tc154730747" 01 非常规空间几何体为载体 PAGEREF _Tc154730747 \h 2
\l "_Tc154730748" 02 立体几何探索性问题 PAGEREF _Tc154730748 \h 4
\l "_Tc154730749" 03 立体几何折叠问题 PAGEREF _Tc154730749 \h 6
\l "_Tc154730750" 04 立体几何作图问题 PAGEREF _Tc154730750 \h 8
\l "_Tc154730751" 05 立体几何建系繁琐问题 PAGEREF _Tc154730751 \h 11
\l "_Tc154730752" 06 两角相等(构造全等)的立体几何问题 PAGEREF _Tc154730752 \h 13
\l "_Tc154730753" 07 利用传统方法找几何关系建系 PAGEREF _Tc154730753 \h 15
\l "_Tc154730754" 08 空间中的点不好求 PAGEREF _Tc154730754 \h 17
\l "_Tc154730755" 09 创新定义 PAGEREF _Tc154730755 \h 20
01 非常规空间几何体为载体
1.(2023·四川南充·模拟预测)如图所示,在圆锥中,为圆锥的顶点,为底面圆圆心,是圆的直径,为底面圆周上一点,四边形是矩形.
(1)若点是的中点,求证:平面;
(2)若,求直线与平面所成角的余弦值.
2.(2023•新高考Ⅱ)如图,三棱锥中,,,,为中点.
(1)证明;
(2)点满足,求二面角的正弦值.
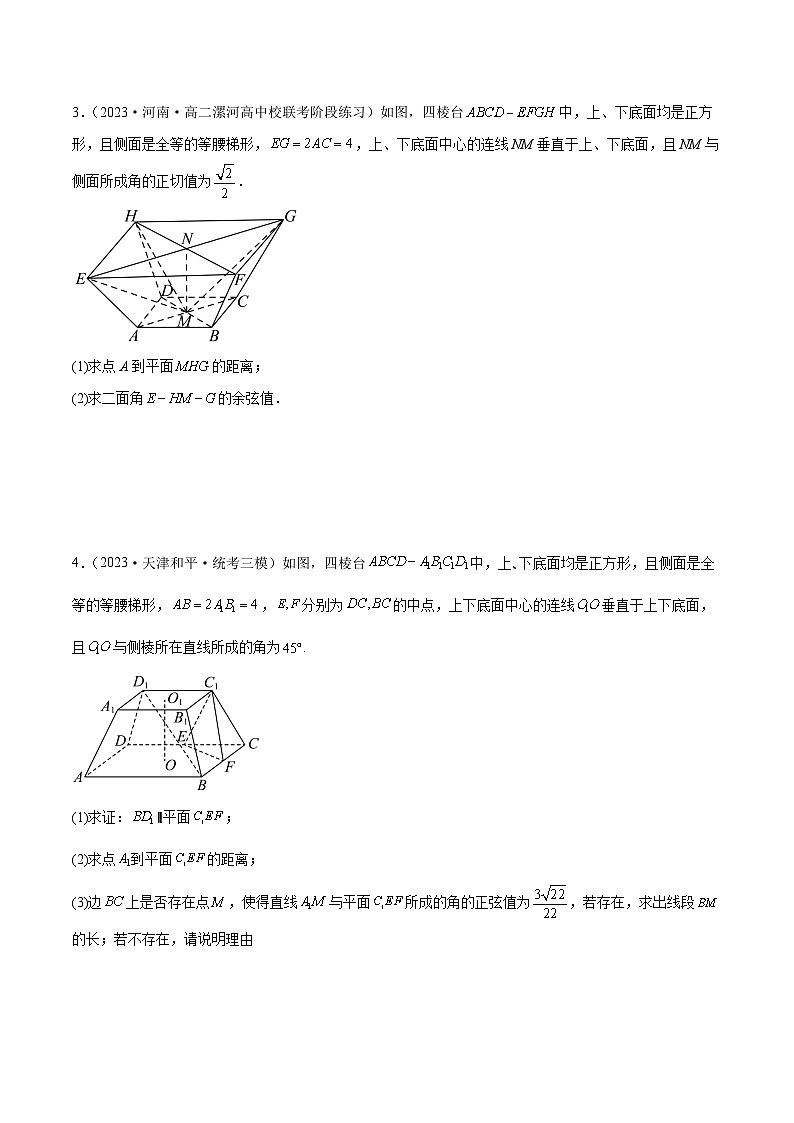
3.(2023·河南·高二漯河高中校联考阶段练习)如图,四棱台中,上、下底面均是正方形,且侧面是全等的等腰梯形,,上、下底面中心的连线NM垂直于上、下底面,且NM与侧面所成角的正切值为.
(1)求点A到平面的距离;
(2)求二面角的余弦值.
4.(2023·天津和平·统考三模)如图,四棱台中,上、下底面均是正方形,且侧面是全等的等腰梯形,,分别为的中点,上下底面中心的连线垂直于上下底面,且与侧棱所在直线所成的角为.
(1)求证:∥平面;
(2)求点到平面的距离;
(3)边上是否存在点,使得直线与平面所成的角的正弦值为,若存在,求出线段的长;若不存在,请说明理由
02 立体几何探索性问题
5.(2023•新高考Ⅰ)如图,在正四棱柱中,,.点,,,分别在棱,,,上,,,.
(1)证明:;
(2)点在棱上,当二面角为时,求.
6.(2023·北京·高三北京八中校考期中)羡除是《九章算术》中记载的一种五面体.如图五面体ABCDEF,四边形ABCD与四边形ADEF均为等腰梯形,其中,,,,M为AD中点,平面BCEF与平面ADEF交于EF.再从条件①,条件②,条件③中选择一个作为已知,使得羡除ABCDEF能够确定,然后解答下列各题:
(1)求证:平面CDE;
(2)求二面角的余弦值.
(3)在线段AE上是否存在点Q,使得MQ与平面ABE所成的角的正弦值为,若存在,求出的值,若不存在,请说明理由.
条件①:平面平面ABCD;
条件②:平面平面ABCD;
条件③:.
7.(2021•甲卷)已知直三棱柱中,侧面为正方形,,,分别为和的中点,为棱上的点,.
(1)证明:;
(2)当为何值时,面与面所成的二面角的正弦值最小?
8.(2021•北京)如图,在正方体,为的中点,交平面交于点.
(Ⅰ)求证:为的中点;
(Ⅱ)若点是棱上一点,且二面角的余弦值为,求的值.
9.(2023·全国·高三专题练习)如图,正方形ADEF所在平面和等腰梯形ABCD所在平面相互垂直,已知.
(1)求证:;
(2)在线段BE上是否存在一点P,使得平面平面BCEF?若存在,求出的值;若不存在,请说明理由.
03 立体几何折叠问题
10.(2023·江苏苏州·高三苏州市相城区陆慕高级中学校考阶段练习)已知图①中四边形是圆的内接四边形,沿将所在圆面翻折至如图②所示的位置,使得.
(1)若,证明:;
(2)若,求二面角余弦值的最小值.
11.(2023·湖南·校联考模拟预测)如图,在梯形中,,,,,与交于点,将沿翻折至,使点到达点的位置.
(1)证明:;
(2)若平面PBC与平面PBD的夹角的余弦值为,求三棱锥的体积.
12.(2023·贵州·高二校联考阶段练习)如图1,已知是直角梯形,,,,C、D分别为BF、AE的中点,,,将直角梯形ABFE沿CD翻折,使得二面角的大小为60°,如图2所示,设N为BC的中点.
(1)证明:;
(2)若M为AE上一点,且,则当为何值时,直线BM与平面ADE所成角的正弦值为.
13.(2023·河南·校联考模拟预测)如图,在矩形中,点在边上,且满足,将沿向上翻折,使点到点的位置,构成四棱锥.
(1)若点在线段上,且平面,试确定点的位置;
(2)若,求锐二面角的大小.
04 立体几何作图问题
14.(2023·贵州·校联考模拟预测)如图,已知平行六面体的底面是菱形,,,且.
(1)试在平面内过点作直线,使得直线平面,说明作图方法,并证明:直线;
(2)求平面与平面所成锐二面角的余弦值.
15.(2023·重庆九龙坡·高三重庆市育才中学校考阶段练习)已知四棱锥中,底面为正方形,O为其中心,点E为侧棱的中点.
(1)作出过O、P两点且与平行的四棱锥截面(在答题卡上作出该截面与四棱锥表面的交线,并写出简要作图过程);记该截面与棱的交点为M,求出比值(直接写出答案);
(2)若四棱锥的侧棱与底面边长均相等,求与平面所成角的正弦值.
16.(2023·全国·高三专题练习)如图,已知底面为平行四边形的四棱锥中,平面与直线和直线平行,点为的中点,点在上,且.
(1)求证:四边形是平行四边形;
(2)求作过作四棱锥的截面,使与截面平行(写出作图过程,不要求证明).截面的定义:用一个平面去截一个几何体,平面与几何体的表面的交线围成的平面图形.
17.(2023·安徽马鞍山·统考三模)如图多面体中,面面,为等边三角形,四边形为正方形,,且,,分别为,的中点.
(1)求二面角的余弦值;
(2)作平面FHG与平面ABCD的交线,记该交线与直线AB交点为P,写出的值(不需要说明理由,保留作图痕迹).
18.(2023·北京·北京市十一学校校考三模)四棱锥中,底面是边长为2的菱形,.,且平面,,点分别是线段上的中点,在上.且.
(Ⅰ)求证:平面;
(Ⅱ)求直线与平面的成角的正弦值;
(Ⅲ)请画出平面与四棱锥的表面的交线,并写出作图的步骤.
05 立体几何建系繁琐问题
19.(2023·浙江台州·高一统考期末)如图,平面平面,四边形为矩形,且为线段上的动点,,,,.
(1)当为线段的中点时,
(i)求证:平面;
(ii)求直线与平面所成角的正弦值;
(2)记直线与平面所成角为,平面与平面的夹角为,是否存在点使得?若存在,求出;若不存在,说明理由.
20.(2023·江苏南京·高一南京外国语学校校考阶段练习)如图,在梯形中,,,,四边形为矩形, 平面平面,.
(1)求证:平面;
(2)求二面角的平面角的余弦值;
(3)若点在线段上运动,设平面与平面所成二面角的平面角为,试求的范围.
21.(2023·重庆·统考三模)如图,四面体ABCD的顶点都在以AB为直径的球面上,底面BCD是边长为的等边三角形,球心O到底面的距离为1.
(1)求球O的表面积;
(2)求二面角的余弦值.
22.(2023·浙江·高二校联考阶段练习)如图所示,在平行四边形ABCD中,,,E为边AB的中点,将沿直线DE翻折为,若F为线段的中点.在翻折过程中,
(1)求证:平面;
(2)若二面角,求与面所成角的正弦值.
23.(2023·浙江杭州·高三浙江省杭州第二中学校考阶段练习)四面体中,,,,,E为AC中点.
(1)证明:;
(2)若二面角的余弦值为,求a的值.
06 两角相等(构造全等)的立体几何问题
24.(2023·河南·统考模拟预测)如图,在三棱锥中,是等边三角形,,点是 的中点,连接.
(1)证明:平面平面;
(2)若,且二面角为,求直线与平面所成角的正弦值.
25.(2023·广东广州·统考一模)如图,在三棱锥中,是等边三角形,,点P是AC的中点,连接BP,DP
证明:平面平面BDP;
若,,求三棱锥的体积.
26.(2023·福建龙岩·统考一模)如图,在三棱锥中,为等边三角形,,面积是面积的两倍,点在侧棱上.
(1)若,证明:平面平面;
(2)若二面角的大小为,且为的中点,求直线与平面所成角的正弦值.
27.(2023·浙江宁波·高三统考期末)如图所示,四面体中,是正三角形,是直角三角形,是的中点,且.
(1)求证:平面;
(2)过的平面交于点,若平面把四面体分成体积相等的两部分,求二面角的余弦值.
07 利用传统方法找几何关系建系
28.(2023·江苏徐州·高三统考期中)如图,在三棱锥中,侧面是锐角三角形,,平面平面.
(1)求证:;
(2)设,点在棱(异于端点)上,当三棱锥体积最大时,若二面角大于,求线段长的取值范围.
29.(2023·江苏常州·高三统考期中)已知三棱柱,,,为线段上的点,且满足.
(1)求证:平面;
(2)求证:;
(3)设平面平面,已知二面角的正弦值为,求的值.
30.(2023·浙江·高三校联考阶段练习)在正三棱台中,侧棱长为1,且为的中点,为上的点,且.
(1)证明:平面,并求出的长;
(2)求平面与平面夹角的余弦值.
31.(2023·湖南永州·统考一模)如图所示,在四棱锥中,底面为矩形,侧面为正三角形,且分别为的中点,在线段上,且.
(1)求证:平面;
(2)当时,求平面与平面的夹角的余弦值.
08 空间中的点不好求
32.(2023·云南临沧·高二校考期中)已知四棱锥,底面为菱形,为上的点,过的平面分别交于点,且∥平面.
(1)证明:;
(2)当为的中点,与平面所成的角为,求平面与平面所成的锐二面角的余弦值.
33.(2023·浙江·高三浙江省新昌中学校联考期中)如图,在四棱台中,底面是边长为2的菱形,,平面平面,点分别为的中点,均为锐角.
(1)求证:;
(2)若异面直线与所成角正弦值为,四棱锥的体积为1,求二面角的平面角的余弦值.
34.(2023·广东·高三茂名市第一中学校联考阶段练习)如图,已知四棱锥中,底面是矩形,,,.
(1)求证:平面平面;
(2)求直线与平面所成角的正弦值.
35.(2023·湖北·高三黄冈中学校联考阶段练习)如图,在几何体中,底面为以为斜边的等腰直角三角形.已知平面平面,平面平面平面.
(1)证明:平面;
(2)若,设为棱的中点,求当几何体的体积取最大值时与所成角的正切值.
36.(2023·全国·模拟预测)如图,已知四边形为正方形,为正方形对角线的交点,平面平面,.
(1)求证:平面平面;
(2)求平面和平面所成角的余弦值的最小值.
37.(2023·重庆·高三重庆八中校考阶段练习)如图甲是由梯形,组成的一个平面图形,其中,,,,.如图乙,将其沿,折起使得与重合,连接,直线与平面所成角为60°.
(1)证明:;
(2)求图乙中二面角的正弦值.
09 创新定义
38.(2023·安徽合肥·合肥一六八中学校考模拟预测)已知顶点为S的圆锥面(以下简称圆锥S)与不经过顶点S的平面α相交,记交线为C,圆锥S的轴线l与平面α所成角θ是圆锥S顶角(圆S轴截面上两条母线所成角θ的一半,为探究曲线C的形状,我们构建球T,使球T与圆锥S和平面α都相切,记球T与平面α的切点为F,直线l与平面α交点为A,直线AF与圆锥S交点为O,圆锥S的母线OS与球T的切点为M,,.
(1)求证:平面SOA⊥平面α,并指出a,b,关系式;
(2)求证:曲线C是抛物线.
39.(2023·辽宁沈阳·东北育才学校校考二模)蜂房是自然界最神奇的“建筑”之一,如图1所示.蜂房结构是由正六棱柱截去三个相等的三棱锥,,,再分别以,,为轴将,,分别向上翻转,使,,三点重合为点所围成的曲顶多面体(下底面开口),如图2所示.蜂房曲顶空间的弯曲度可用曲率来刻画,定义其度量值等于蜂房顶端三个菱形的各个顶点的曲率之和,而每一顶点的曲率规定等于减去蜂房多面体在该点的各个面角之和(多面体的面角是多面体的面的内角,用弧度制表示).例如:正四面体在每个顶点有3个面角,每个面角是,所以正四面体在各顶点的曲率为.
(1)求蜂房曲顶空间的弯曲度;
(2)若正六棱柱底面边长为1,侧棱长为2,设
(i)用表示蜂房(图2右侧多面体)的表面积;
(ii)当蜂房表面积最小时,求其顶点的曲率的余弦值.
40.(2023·全国·高三校联考专题练习)设P为多面体M的一个顶点,定义多面体M在点P处的离散曲率为,其中Qi(i=1,2,…,k,k≥3)为多面体M的所有与点P相邻的顶点,且平面Q1PQ2,平面Q2PQ3,…,平面Qk﹣1PQk和平面QkPQ1遍历多面体M的所有以P为公共点的面.
(1)如图1,已知长方体A1B1C1D1﹣ABCD,AB=BC=1,,点P为底面A1B1C1D1内的一个动点,则求四棱锥P﹣ABCD在点P处的离散曲率的最小值;
(2)图2为对某个女孩面部识别过程中的三角剖分结果,所谓三角剖分,就是先在面部取若干采样点,然后用短小的直线段连接相邻三个采样点形成三角形网格.区域α和区域β中点的离散曲率的平均值更大的是哪个区域?(确定“区域α”还是“区域β”)
41.(2023·全国·校联考模拟预测)蜂房是自然界最神奇的“建筑”之一,如图1所示.蜂房结构是由正六棱柱截去三个相等的三棱锥,,,再分别以,,为轴将,,分别向上翻转,使,,三点重合为点所围成的曲顶多面体(下底面开口),如图2所示.蜂房曲顶空间的弯曲度可用曲率来刻画,定义其度量值等于蜂房顶端三个菱形的各个顶点的曲率之和,而每一顶点的曲率规定等于减去蜂房多面体在该点的各个面角之和(多面体的面角是多面体的面的内角,用弧度制表示).
(1)求蜂房曲顶空间的弯曲度;
(2)若正六棱柱的侧面积一定,当蜂房表面积最小时,求其顶点的曲率的余弦值.
相关试卷
这是一份【二轮复习】高考数学专题17 圆锥曲线常考压轴小题全归类(考点专练)(原卷版+解析版),文件包含二轮复习高考数学专题17圆锥曲线常考压轴小题全归类考点专练原卷版docx、二轮复习高考数学专题17圆锥曲线常考压轴小题全归类考点专练解析版docx等2份试卷配套教学资源,其中试卷共60页, 欢迎下载使用。
这是一份【二轮复习】高考数学专题20 概率与统计常考小题归类(考点专练)(原卷版+解析版),文件包含二轮复习高考数学专题20概率与统计常考小题归类考点专练原卷版docx、二轮复习高考数学专题20概率与统计常考小题归类考点专练解析版docx等2份试卷配套教学资源,其中试卷共49页, 欢迎下载使用。
这是一份【二轮复习】高考数学专题21 概率与统计的综合运用(考点专练)(原卷版+解析版),文件包含二轮复习高考数学专题21概率与统计的综合运用考点专练原卷版docx、二轮复习高考数学专题21概率与统计的综合运用考点专练解析版docx等2份试卷配套教学资源,其中试卷共75页, 欢迎下载使用。









