专题02 旋转问题-【中考冲刺】最新中考数学二轮复习名校模拟题重要考点分类汇编（江苏专用）

这是一份专题02 旋转问题-【中考冲刺】最新中考数学二轮复习名校模拟题重要考点分类汇编（江苏专用），文件包含专题02旋转问题原卷版docx、专题02旋转问题解析版docx等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。
1．（2023·江苏宿迁·统考一模）如图，在中，．将绕顶点C旋转得到，若点O是中点，点P是中点，在旋转过程中，线段的最大值等于（ ）
A．4B．6C．8D．10
【答案】B
【分析】连接，进而得到，当三点共线时，线段的值最大，进行求解即可．
【详解】解：∵，
∴，
∵将绕顶点C旋转得到，点O是中点，
∴，，
连接，
∵点P是中点，
∴，
∵，
∴当三点共线时，线段的值最大．
故选：B．
2．（2023春·江苏无锡·九年级校联考期末）如图，点A的坐标为，点B是x轴负半轴上的一点，将线段绕点A按顺时针方向旋转得到线段．若点C的坐标为，则m的值为（ ）
A．B．C．D．
【答案】D
【分析】过C作轴于点D，轴于点E，根据将线段AB绕点A按逆时针方向旋转得到线段AC，可得是等边三角形，又，可表示出，用勾股定理表示出有关线段的长，根据列方程求解即可．
【详解】解：过C作轴于点D，轴于点E，如图：
∵轴，轴，，
∴四边形是矩形，
∵将线段绕点A按顺时针方向旋转得到线段，
∴，
∴是等边三角形，
∴，
∵，
∴，
∴，
∴，
在中，，
在中，，
∵，
∴，
化简变形得：，
解得（舍去）或，
∴，
故选：D．
二、填空题
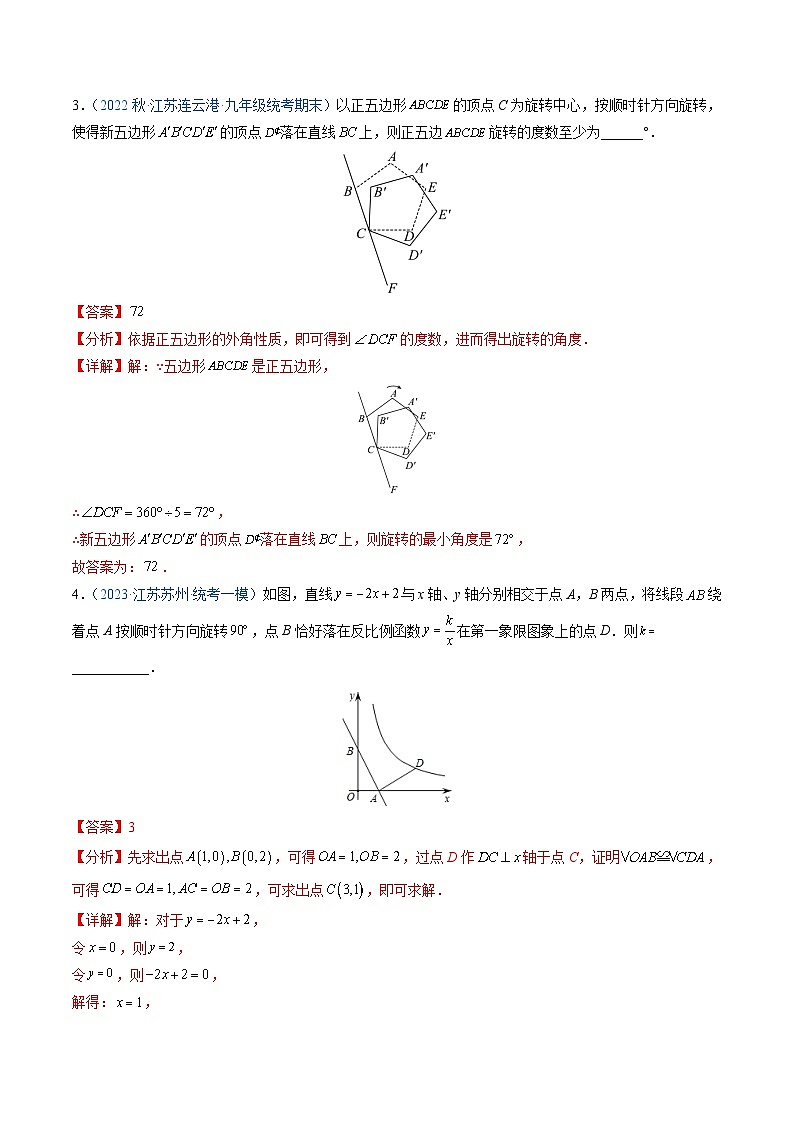
3．（2022秋·江苏连云港·九年级统考期末）以正五边形的顶点C为旋转中心，按顺时针方向旋转，使得新五边形的顶点落在直线上，则正五边旋转的度数至少为______°．
【答案】
【分析】依据正五边形的外角性质，即可得到的度数，进而得出旋转的角度．
【详解】解：∵五边形是正五边形，
∴，
∴新五边形的顶点落在直线上，则旋转的最小角度是，
故答案为：．
4．（2023·江苏苏州·统考一模）如图，直线与x轴、y轴分别相交于点A，B两点，将线段绕着点A按顺时针方向旋转，点B恰好落在反比例函数在第一象限图象上的点D．则___________．
【答案】3
【分析】先求出点，可得，过点D作轴于点C，证明，可得，可求出点，即可求解．
【详解】解：对于，
令，则，
令，则，
解得：，
∴点，
∴，
如图，过点D作轴于点C，
根据题意得：，，
∴，
∵，
∴，
∵，
∴，
∴，
∴，
∴点，
把代入得：．
故答案为：3
5．（2023春·江苏泰州·九年级校考阶段练习）第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素．如图，这个图案绕着它的中心旋转角后能够与它本身重合，则角α至少为______度．
【答案】60
【分析】先求出正六边形的中心角，再根据旋转变换的性质解答即可．
【详解】解：，
则这个图案绕着它的中心旋转后能够与它本身重合，
故答案为：60．
6．（2022秋·江苏盐城·九年级校考阶段练习）已知直角三角形ABC的一条直角边cm，斜边cm，则以为轴旋转一周，所得到的圆锥的侧面积是______．
【答案】
【分析】根据勾股定理求得底面半径，然后求得底面积，再利用扇形面积求解即可．
【详解】解：∵直角三角形的一条直角边cm、斜边cm,
，
∴圆锥的侧面积，
故答案为：．
7．（2022秋·江苏宿迁·九年级校考期末）如图，、是的直径，点在上，，点从点出发沿顺时针方向绕圆心旋转，当__________时，直径在中截得的三角形与相似．
【答案】50或70或160
【分析】是的直径，得到，当时，时，时，直径在中截得的三角形与相似，分三种情况讨论求解即可．
【详解】解：∵是的直径，
∴；
①当时，交于点，则：，
∵，
∴，满足题意；
连接，
∵，
∴，
∴，
∴；
②当时，交于点，则：，
∵，
∴，满足题意；
此时：，
∴；
③时，于点，则，
∵，
∴，满足题意；
此时：，
∴，
∴．
综上：当50或70或160时，直径在中截得的三角形与相似．
故答案为：50或70或160．
8．（2023秋·江苏南京·九年级统考期末）将函数的图像绕着原点旋转，得到的新图像的函数表达式为_________．
【答案】
【分析】将其绕顶点旋转后，开口大小不变，顶点坐标和开口方向都发生变化，确定顶点坐标即可得出所求的结论．
【详解】解：二次函数的顶点坐标为,
图象绕着顶点旋转后，开口大小不变，顶点坐标变为，开口方向相反，
即，
则旋转后的二次函数解析式是：．
故答案为：
三、解答题
9．（2022秋·江苏连云港·九年级统考期末）已知二次函数的图象经过点，．
(1)求二次函数的表达式；
(2)点P为二次函数图象上一点，点F在y轴正半轴上，将线段绕点P逆时针旋转得到，点E恰好落在x轴正半轴上，求点P的坐标．
【答案】(1)二次函数的表达式为；
(2)．
【分析】（1）利用待定系数法即可求解；
（2）过点P作轴于点M，轴于点N，证明，推出，据此求解即可．
【详解】（1）解：∵二次函数的图象经过点，，
∴，解得，
∴二次函数的表达式为；
（2）解：过点P作轴于点M，轴于点N，
∵，
∴四边形为矩形，
∴即，
∵将线段绕点P逆时针旋转得到，
∴且，即，
∴，
∴，
∴，
设，则，
解得，
∴．
10．（2023春·江苏盐城·九年级校考阶段练习）如图1，一台灯放置在水平桌面上，底座与桌面垂直，底座高，连杆，，与始终在同一平面内．
(1)如图2，转动连杆，，使成平角，，求连杆端点离桌面的高度．
(2)将图2中的连杆再绕点逆时针旋转，如图3，此时连杆端点D离桌面l的高度减小了多少？(参考数据：，，）
【答案】(1)此时连杆端点D离桌面l的高度为
(2)此时连杆端点D离桌面l的高度减小了
【分析】（1）过点作于点，利用矩形的性质和锐角三角函数求得和长，从而可得长；
（2）过点作于点，过点作于点，过点作于点，于点，根据矩形的性质和锐角三角函数求得、、，从而可得长．
【详解】（1）解：过点作于点，则，
，，
，
四边形是矩形，
，，
，
，
在中，，即，
，
，
此时连杆端点离桌面的高度为；
（2）解：过点作于点，过点作于点，过点作于点，于点，则四边形为矩形，
，，
，
，
，
，
，
下降的高度为，
答：此时连杆端点离桌面的高度减小了．
11．（2023秋·江苏南通·九年级统考期末）定义：平面直角坐标系中，若点绕原点顺时针旋转，恰好落在函数图象上，则称点为函数图象的“直旋点”．例如，点是函数图象的“直旋点”．
(1)在①，②，③三点中，是一次函数图象的“直旋点”的有_____（填序号）；
(2)若点为反比例函数图象的“直旋点”，求的值；
(3)二次函数与轴交于两点（A在的左侧），与轴交于点，点是二次函数图象的“直旋点”且在直线上，求点坐标．
【答案】(1)②③
(2)
(3)或
【分析】（1）分别写出三个点绕原点顺时针旋转得到的点的坐标，逐个验证是否在一次函数图象上即可；
（2）把点绕原点顺时针旋转得到的点的坐标代入即可得到答案；
（3）先求出点A、B、C的坐标，再求出直线的解析式，设点D的坐标为，则点D绕原点顺时针旋转得到点，根据点是二次函数图象的“直旋点”且在直线上，得到关于m、n的方程组，解方程组即可得到点D的坐标．
【详解】（1）解：①绕原点顺时针旋转得到，
当时，，故不是一次函数图象的“直旋点”，
②绕原点顺时针旋转得到，
当时，，故是一次函数图象的“直旋点”，
③绕原点顺时针旋转得到，
当时，，故是一次函数图象的“直旋点”，
故答案为：②③
（2）点绕原点顺时针旋转得到，
∵点为反比例函数图象的“直旋点”，
∴点满足，代入可得，，
解得；
（3）当时， ，解得
∴点，
当时，，
∴点,
设直线的解析式为，
则
解得，
∴直线的解析式为，
设点D的坐标为，则点D绕原点顺时针旋转得到点，
∵点是二次函数图象的“直旋点”且在直线上，
∴点在二次函数图象上，在直线上，
∴，
解得，，
∴点坐标为或
12．（2023秋·江苏扬州·九年级统考期末）如图，在中，，正方形的边长为2，将正方形绕点B旋转一周，连接．
(1)请找出图中与相似的三角形，并说明理由；
(2)求当A、E、F三点在一直线上时的长．
【答案】(1)，理由见解析
(2)或
【分析】（1）先根据正方形的性质和勾股定理得到，，再根据等腰直角三角形的性质
和勾股定理得到，，进而证明，，由此即可
证明；
（2）先利用勾股定理求出，进而求出，再分当在左上方时，当在右下
方时，两种情况求出的长，然后利用相似三角形的性质求解即可．
【详解】（1）解：，理由如下：
∵四边形是正方形，
∴，，
∴，
∵，
∴，，
∴，即，
又∵，
∴；
（2）解：∵，
∴，
∵当A、E、F三点在一直线上时，，
∴，
如图1，当在左上方时，
∴，
∵，
∴，
∴；
如图2，当在右下方时，
∴
∵，
∴，
∴；
综上所述，当A、E、F三点在一直线上时，的长为或．
13．（2023秋·江苏·九年级统考期末）如图1，中，，点D，E分别是的中点，连接．将绕点C逆时针旋转得到（如图2），连接，．
(1)求证：；
(2)已知，，分别延长，交于点F．
①若，求BF的长；
②连接FC，若，直接写出的值．
【答案】(1)见解析
(2)①②
【分析】（1）利用两边成比例及其夹角相等证明相似即可；
（2）①证明，可得，再根据勾股定理可得答案；
②作交于点N，证明得到，进而求得，即可得出答案．
【详解】（1）证明：∵点D，E分别是的中点，
∴，，
∴，即，
又∵，
∴，
∴；
（2）①如图，设交于点G，
∵，，，
∴，
由（1）得，
∴，
又∵，
∴，
∴，
∴．
②作交于点N，
，
，
，
，
，
，，
，
，
．
14．（2023春·江苏南通·九年级南通田家炳中学校考开学考试）如图，反比例函数的图象与一次函数的图象交于，两点，点的坐标为，点的坐标为．
(1)求反比例函数的关系式与的值；
(2)求不等式的解集（直接写出答案）；
(3)线段绕点顺时针旋转90°，得到线段，求点经过的路径长．
【答案】(1)反比例函数的关系式为，
(2)或
(3)
【分析】（1）把点A的坐标为，代入可求出反比例函数的关系式，进而确定点B的坐标，得出答案；
（2）根据图象直接得出答案；
（3）直接用弧长公式求点经过的路径长．
【详解】（1）把点A的坐标为，代入反比例函数得，
，解得
∴反比例函数的关系式为，
点的坐标为代入得，，
∴反比例函数的关系式为，；
（2）根据两个函数的图象，可得，
不等式的解集为：或，
（3）∵线段绕点顺时针旋转90°，得到线段，
∴点经过的路径是以为圆心，长为半径的圆上圆心角为90°的一条弧，
∵点A的坐标为，点的坐标为，
∴，
∴点经过的路径长为．
15．（2023秋·江苏南通·九年级统考期末）如图，在平面直角坐标系中，，，将线段AB绕原点O逆时针旋转到．
(1)求点的坐标；
(2)求点B运动的路径长．
【答案】(1)
(2)
【分析】（1）连接、，作轴于点，轴于点，可证明，得，，则点的坐标是；
（2）由旋转得，，以点为圆心，的长为半径作，根据弧长公式求出的长，就是点运动的路径长．
【详解】（1）解：连接、，作轴于点，轴于点，则，
将线段绕原点逆时针旋转到，
，，
，
在和中，
，
，
，
，，
点在第二象限，
点的坐标是．
（2）由旋转得，，
以点为圆心，的长为半径作，则点运动的路径长为的长，
作轴于点，
，
，，
，
，
点运动的路径长是．
16．（2023春·江苏盐城·九年级校考阶段练习）如图1，直线与x轴交于点B，与y轴交于点C，抛物线经过B、C两点，且与x轴交于另一点A．
(1)求抛物线的解析式；
(2)如图2，点E的坐标为，经过点A的直线与该抛物线交于点F，点P是直线上的一个动点，连接、、，记的面积为，的面积为，那么的值是否是定值？如果是，请求出这个定值；如果不是，请说明理由．
(3)如图3，点Q是直线上方的抛物线上的动点（不与点B、C重合），过Q作轴交于点G，作于点H，求的周长的最大值．
(4)当（3）中的周长取得最大值时，将绕着点G旋转一周，在旋转的过程中，点Q、G、H的对应点分别记为、、．当点恰好落在坐标轴上时，请直接写出相应的点坐标．
【答案】(1)
(2)是定值，
(3)的周长的最大值
(4)的坐标为或或
【分析】（1）求出、两点坐标，再将这两点代入即可求解；
（2）先由题意确定直线，过点作轴交于点，过点作轴交于点，则，，则，分别求出、即可求解；
（3）延长交轴于点，由题意可得，则，，的周长，要求的周长最大值，求出的最大值即可，设，则，则，可求的最大值为2，则可求的周长最大值；
（4）分两种情况讨论：①当在轴上时，此时轴，过点作交于，由，利用三角形函数可求，；②当在轴上，设点横坐标为，由，可求，或，；当，时，过点作交的延长线于点，过点作轴交于点，先证明，设，可得，可求；当，时，过点作交于，过点作交于，证明，设，可得，求出．
【详解】（1）解：对于，令，则，
，
令，则，
，
抛物线经过、两点，
，
解得，
；
（2）解：是定值，理由如下：
令，则，
解得或，
，
直线经过点，
，
，
过点作轴交于点，过点作轴交于点，如图1，
，
，
，
，，
，，
，
是定值；
（3）解：延长交轴于点，如图2，
，
，
，
，，
，
，，
，，
的周长，
设，则，
，
当时，有最大值2，
的周长的最大值；
（4）解：由（3）可得，
，
，
，，
，，
如图3，
当在轴上时，
轴，
过点作交于，
，
，，
，，
；
②当在轴上，
设点横坐标为，
，
，
或，
，或，，
当，时，如图4，
过点作交的延长线于点，过点作轴交于点，
，
，，
，
，
，
设，
，
解得，，
；
当时，如图5，
过点作交于，过点作交于，
，
，，
，
，
，
设，
，
解得，，
；
综上所述：的坐标为或或．
17．（2022秋·江苏连云港·九年级统考期末）如图，是等边的外接圆，过点A作的垂线交于点H．
(1)若点G是劣弧上一点（不与点B、C重合），直线交于点D，连接．求证：平分；
(2)在（1）条件下，将绕点A顺时针旋转得到线段．
①若，求证：点F落在射线上；
②若，求线段与线段的数量关系．
【答案】(1)见解析
(2)①见解析；②．
【分析】（1）利用圆周角定理证明，即可得出结论；
（2）①设直线与直线交于点，，推出，得到点与点F重合，即可得出结论；
②连接，作于点N，证明是线段的垂直平分线，、都是等腰直角三角形，分别求得，，据此求解即可．
【详解】（1）证明：∵是等边的外接圆，
∴，
∴，
∴平分；
（2）①证明：设直线与直线交于点，如图，
∵，∴，
∵，，∴，
∵是等边三角形，
∴，
∴，
∴，
∵将绕点A顺时针旋转得到线段，
∴，
∴点与点F重合，
点F落在射线上；
②解：连接，作于点N，与相交于点M，
由（1）得，，
∴，则，
∴，即，
∵将绕点A顺时针旋转得到线段，，
∴，
∴是线段的垂直平分线，
∴，
∵，
∴，
∴，
∴，则是等腰直角三角形，
∴，
∴都是等腰直角三角形，
∴，
∴，
∴，
∴，
∴，
∴．
18．（2022春·江苏淮安·九年级校考阶段练习）如图①，已知抛物线与坐标轴交于三点，其中，的平分线交y轴于点D．
(1)直接填空： ，点A的坐标是 ， °；
(2)点P为抛物线的对称轴上一动点，若为等腰三角形，求出点P的坐标；
(3)过点D的直线与线段分别交于点M，N．试问：是否为定值？如果是，请求出该值；如果不是，说明理由；
(4)等腰的斜边，将如图②放置，使与重合，与相交于G，设的中点为F．若绕点F顺时针旋转（如图③），在从到的变化过程中，点G相应移动的总路程为 ．
【答案】(1)； ；
(2)点P的坐标为或
(3)是，
(4)
【分析】（1）由点的坐标为,可知，故此可求得的值，然后令得到关于的方程，解关于的方程可得到点的坐标，最后利用正切值求的度数、抛物线的对称性可确定出抛物线的对称轴；
（2）利用特殊锐角三角函数值可求得，则可得到点的坐标.设点的坐标为，依据两点的距离公式可求得的长，然后分为三种情况列方程求解即可；
（3）设直线的解析式为，接下来求得点和点的横坐标，于是可得到的长，然后利用特殊锐角三角函数值可求得的长，最后将和的长代入化简即可；
（4）求出两个特殊位置的值，即可解决问题．
【详解】（1）解：
，解得：
令得：，
又，
，解得： 或．
点A的坐标为，
则，，
，
故的度数，
故答案为：；；；
（2）解：，，
，
．
为的平分线，
．
．
点D的坐标为
设点P的坐标为．
依据两点间的距离公式可知：．
当时，，方程无解．
当时，，解得或，
当时，点A，点D，点P三点共线，
不合题意舍去，
点P的坐标为．
当时，，解得．
点P的坐标为．
综上所述，点P的坐标为或．
（3）解：是；
设直线的解析式为，将点A的坐标代入得： ，解得
直线的解析式为．
设直线的解析式为．
把代入得：，解得： ，
点的坐标为
将与联立解得： ．
点M的横坐标为：．
过点M作轴，垂足为G．则
，
（4）解：如图，当O与R重合时，过点G作于M．
在中，，
，
，
，
设，则
，
，
如图，当时，的值最大，过点F作于N．
，，
，
，
，
，
，
如图4﹣3中，当点R落在上时，的值最小，此时，
观察图象可知，的长开始是增大，最大值为，然后减小，最小值为，
点G的运动路径的长
故答案为：
19．（2023·江苏苏州·统考一模）（1）如图①，在正方形中，E，F分别是，边上的动点，且，将绕点D逆时针旋转90°，得到，可以证明，进一步推出，，之间的数量关系为______________；
（2）在图①中，连接分别交和于P，Q两点， 求证：；
（3）如图②，在菱形中，，点E，F分别是边，上的动点（不与端点重合），且，连接分别与边，交于M，N．当时，猜想，，之间存在什么样的数量关系，并证明你的结论．
【答案】（1）（2）见解析；（3），证明见解析
【分析】（1）证明，可得出和的数量关系，即可得出结论；
（2）根据正方形的性质可证明和即可证明；
（3）将绕点A顺时针旋转，此时与重合，F转到点G，在上取，连接，利用证明，再证明是直角三角形即可
【详解】解：（1），理由如下：
∵将绕点D逆时针旋转90°，得到，
∴
三点共线，
在和中，
∴
；
（2）如图，
由（1）知：，
，
又四边形是正方形，
，
是正方形的对角线，
，
,
又，
又，
；
（3）将绕点A顺时针旋转，此时与重合，F转到点G，在上取，连接，如图，
∴
又
∵菱形
中，
20．（2023秋·江苏南京·九年级校考期末）如图1，点O为直线上一点，过O点作射线，使，将一直角三角板的直角顶点放在点O处，一边在射线上，另一边在直线的下方．
(1)如图2，将图1中的三角板绕点O逆时针旋转，使边在的内部，且恰好平分．此时 度；
(2)如图3，继续将图2中的三角板绕点O按逆时针方向旋转，使得在的内部．试探究与之间满足什么等量关系，并说明你的理由；
(3)将图1中的三角板绕点O按每秒12°的速度沿逆时针方向旋转一周，在旋转过程中，若直线恰好平分，则此时三角板绕点O旋转的时间是多少秒？
(4)将图1中的三角板绕点O按每秒12°的速度沿逆时针方向旋转，同时射线绕点O以每秒2°的速度沿逆时针方向旋转，旋转30秒后都停止．在旋转的过程中，若直线恰好平分，则此时三角板绕点O旋转的时间是 秒．（直接写出答案）
【答案】(1)
(2)，理由见解析
(3)秒或秒
(4)秒或秒
【分析】（1）先根据角平分线的定义得到，再根据平角的定义即可得到；
（2）先根据平角的定义求出，再由即可得到结论；
（3）设三角板绕点O旋转的时间是t秒，先求出，然后分当在外部时，当在内部时，两种情况求出对应的旋转角度，然后建立方程求解即可；
（4）设三角板绕点O旋转的时间是m秒，先求出，然后分当在外部时，当在内部时，两种情况求出对应的旋转角度，然后建立方程求解即可．
【详解】（1）解：∵恰好平分，
∴，
∴．
故答案为：；
（2）解：，理由如下：
∵，
∴，
∵，
∴，
∴；
（3）解：设三角板绕点O旋转的时间是t秒，
∵，
∴，
当在外部时，如图1所示，
∵直线平分，
∴，
∴，
∴此时的旋转角度为，
∴，
解得；
当在内部时，如图2所示，
∵恰好平分，
∴，
∴此时旋转的角度为，
∴，
解得；
综上所述，当直线恰好平分，此时三角板绕点O旋转的时间是秒或秒；
（4）解：运动时间为m秒时，直线恰好平分，
∴，
当在外部时，如图3所示，
∵直线平分，
∴，
∴，
∴此时的旋转角度为，
∴，
解得；
当在内部时，如图4所示，
∵恰好平分，
∴，
∴此时旋转的角度为，
∴，
解得；
综上所述，当直线恰好平分，此时三角板绕点O旋转的时间是秒或秒．