2023-2024学年北京二中高二（下）段考数学试卷

这是一份2023-2024学年北京二中高二（下）段考数学试卷，共21页。试卷主要包含了已知椭圆C等内容，欢迎下载使用。
A. 各点的横坐标缩短到原来的12，再向左平移π3个单位长度
B. 各点的横坐标缩短到原来的12，再向左平移π6个单位长度
C. 各点的横坐标伸长到原来的2倍，再向左平移π3个单位长度
D. 各点的横坐标伸长到原来的2倍，再向左平移π6个单位长度
2.已知等差数列{an}前9项的和为27，a10=8，则a100=( )
A. 100B. 99C. 98D. 97
3.已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是( )
A. 若m//α，n//α，则m//nB. 若α⊥γ，β⊥γ，则α//β
C. 若m//α，m//β，则α//βD. 若m⊥α，n⊥α，则m//n
4.若抛物线y2=2px(p>0)上的点A(x0, 2)到其焦点的距离是A到y轴距离的3倍，则p等于( )
A. 12B. 1C. 32D. 2
5.已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx−ay+2ab=0相切，则C的离心率为( )
A. 63B. 33C. 23D. 13
6.反射性元素的特征是不断发生同位素衰变，而衰变的结果是放射性同位素母体的数目不断减少，但其子体的原子数目将不断增加，假设在某放射性同位素的衰变对程中，其含量N(单位：贝克)与时间t(单位：天)满足函数关系N(t)=N0e−t24(e为自然对数的底数)，其中N0为t=0时该同位素的含量，已知当t=48时，该放射性同位素含量的瞬时变化率为−1，则N(48)=( )
A. 12贝克B. 12e贝克C. 24贝克D. 24e贝克
7.直线y=5x+b是曲线y=x3+2x+1的一条切线，则实数b=( )
A. −1或1B. −1或3C. −1D. 3
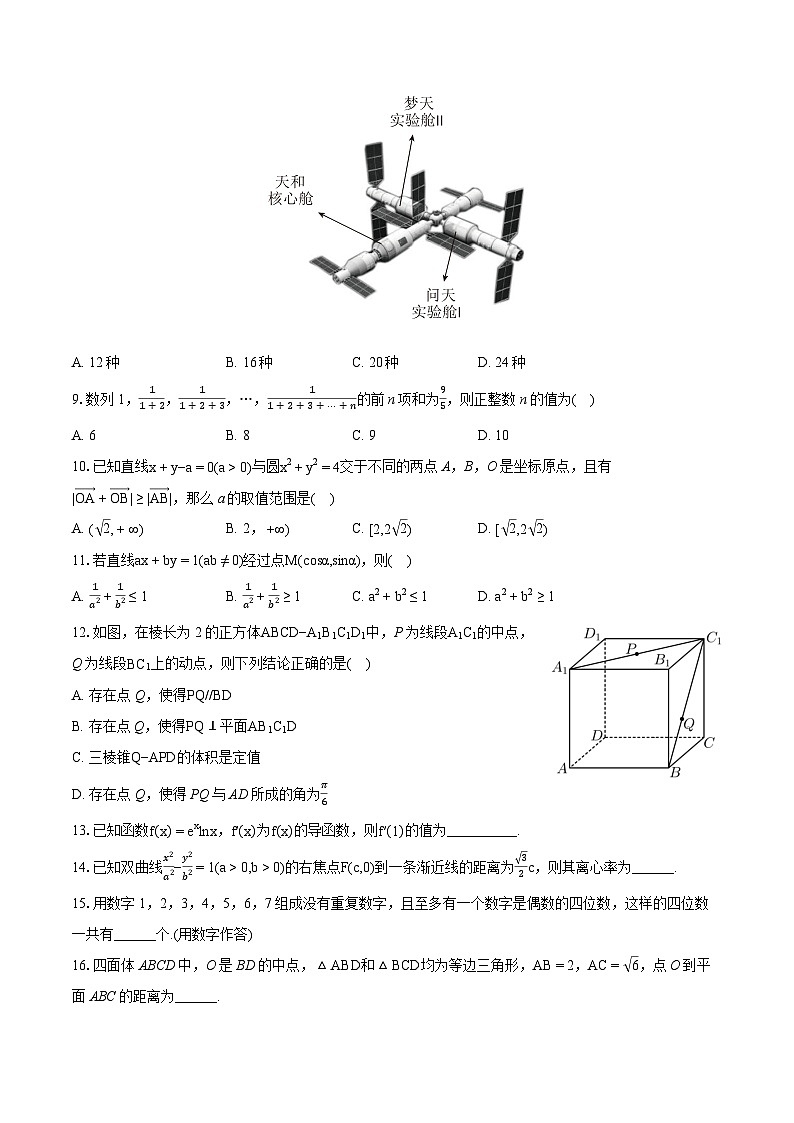
8.如图，中国空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱.假设中国空间站要安排甲，乙，丙，丁，戊，己6名航天员开展实验，其中天和核心舱安排3人，问天实验舱安排2人，梦天实验舱安排1人.若安排甲、乙两人同时在一个舱内做实验，则不同的安排方案共有( )
A. 12种B. 16种C. 20种D. 24种
9.数列1，11+2，11+2+3，…，11+2+3+⋯+n的前n项和为95，则正整数n的值为( )
A. 6B. 8C. 9D. 10
10.已知直线x+y−a=0(a>0)与圆x2+y2=4交于不同的两点A，B，O是坐标原点，且有|OA+OB|≥|AB|，那么a的取值范围是( )
A. ( 2,+∞)B. 2，+∞)C. [2,2 2)D. [ 2,2 2)
11.若直线ax+by=1(ab≠0)经过点M(csα,sinα)，则( )
A. 1a2+1b2≤1B. 1a2+1b2≥1C. a2+b2≤1D. a2+b2≥1
12.如图，在棱长为2的正方体ABCD−A1B1C1D1中，P为线段A1C1的中点，Q为线段BC1上的动点，则下列结论正确的是( )
A. 存在点Q，使得PQ//BD
B. 存在点Q，使得PQ⊥平面AB1C1D
C. 三棱锥Q−APD的体积是定值
D. 存在点Q，使得PQ与AD所成的角为π6
13.已知函数fx=exlnx，f′x为fx的导函数，则f′1的值为__________.
14.已知双曲线x2a2−y2b2=1(a>0,b>0)的右焦点F(c,0)到一条渐近线的距离为 32c，则其离心率为______.
15.用数字1，2，3，4，5，6，7组成没有重复数字，且至多有一个数字是偶数的四位数，这样的四位数一共有______个.(用数字作答)
16.四面体ABCD中，O是BD的中点，△ABD和△BCD均为等边三角形，AB=2，AC= 6，点O到平面ABC的距离为______.
17.在△ABC中，角A，B和C所对的边长为a，b和c，面积为13(a2+c2−b2)，且∠C为钝角，则tanB= (1) ；ca的取值范围是 (2)
18.对于数列{an}，令Tn=a1−a2+a3−a4+⋯+(−1)n+1an，给出下列四个结论：
①若an=n，则T2023=1012；
②若Tn=n，则a2022=−1；
③存在各项均为整数的数列{an}，使得|Tn|>|Tn+1|对任意的n∈N*都成立；
④若对任意的n∈N*，都有|Tn|b>0)的左、右顶点分别为点A，B，且|AB|=4，椭圆C离心率为12.
(Ⅰ)求椭圆C的方程；
(Ⅱ)过椭圆C的右焦点，且斜率不为0的直线l交椭圆C于M，N两点，直线AM，BN的交于点Q，求证：点Q在直线x=4上.
22.已知函数f(x)=x+alnx(a∈R).
(Ⅰ)当a=−1时，求函数f(x)的极值；
(Ⅱ)若不等式f(x)≤12x2+ax对任意x>0恒成立，求a的取值范围．
23.已知有穷数列A：a1，a2，…，aN(N∈N*,N≥3)满足a，∈{−1,0,1}(i=1,2,…，N).给定正整数m，若存在正整数s，t(s≠t)，使得对任意的k∈{0,1,2,…，m−1}，都有as+k=at+k，则称数列A是m−连续等项数列.
(1)判断数列A：−1，1，0，1，0，1，−1是否为3−连续等项数列？是否为4−连续等项数列？说明理由；
(Ⅱ)若项数为N的任意数列A都是2−连续等项数列，求N的最小值；
(Ⅲ)若数列A：a1，a2，…，aN不是4−连续等项数列，而数列A1：a1a2，…，aN，−1，数列A2：a1a2，…，aN，0与数列A3：a1，a2，…，aN，1都是4−连续等项数列，且a3=0，求aN的值.
答案和解析
1.【答案】B
【解析】解：把函数y=sinx的图象上各点的横坐标缩短到原来的12，得到函数y=sin2x的图象，
接下来若向左平移π3个单位长度，得到函数y=sin2(x+π3)=sin(2x+2π3)的图象；
若向左平移π6个单位长度，得到函数y=sin2(x+π6)=sin(2x+π3)的图象；
故A错误，B正确；
C、D中伸长到原来的2倍，得到函数y=sinx2的图象，在无论怎样平移都得不到所要求的函数的图象，
故D错误．
故选：B.
利用函数图象平移、伸缩变换的法则依次判定各个选择支的变化之后的函数解析式是否符合题目要求即可作出判定．
本题主要考查函数y=Asin(ωx+φ)的图象变换规律，属于基础题．
2.【答案】C
【解析】【分析】
本题考查等差数列通项公式和前n项和运算，属于基础题.
由前9项的和和a10，求解首项与公差，进而利用通项公式求解即可.
【解答】
解：由已知9a1+36d=27a1+9d=8，所以a1=−1,d=1,a100=a1+99d=−1+99=98.
故选：C.
3.【答案】D
【解析】【分析】
本题考查空间中线线关系、面面关系判断，考查空间想象能力，属于中档题.
由线面的位置关系可判断A，C；由面面位置关系可判断B；由线面垂直的性质可判断D，进而可得正确选项.
【解答】
解：对于选项A：若m//α，n//α，则m//n，m，n异面或m，n相交，故选项A不正确；
对于选项B：若α⊥γ，β⊥γ，则α//β或α，β相交，故选项B不正确；
对于选项C：若m//α，m//β，则α//β或α，β相交，故选项C不正确；
对于选项D：若m⊥α，n⊥α，由线面垂直的性质可得m//n，故选项D正确.
故选：D.
4.【答案】D
【解析】【分析】
本题主要考查了抛物线的定义和性质．考查了考生对抛物线定义的掌握和灵活应用，属于基础题．
根据抛物线的定义及题意可知3x0=x0+p2，得出x0求得p，可得答案．
【解答】
解：∵抛物线y2=2px(p>0)上的点A(x0, 2)到其焦点的距离是A到y轴距离的3倍，
则3x0=x0+p2，∴x0=p4，
∴p22=2，
∵p>0，
∴p=2，
故选D.
5.【答案】A
【解析】【分析】
本题考查了椭圆的性质，点到直线的距离公式，考查了计算能力，属于中档题．
根据题意，可得2ab a2+b2=a，进而求得离心率．
【解答】解：以线段A1A2为直径的圆与直线bx−ay+2ab=0相切，
∴原点到直线bx−ay+2ab=0的距离等于a，
即2ab a2+b2=a，
化为a2=3b2，
∴椭圆C的离心率e=ca= 1−b2a2= 63.
故选A.
6.【答案】C
【解析】【分析】
本题主要考查函数的瞬时变化率的求解，指数函数模型的实际应用，属于基础题．
先对函数求导，结合已知可求出N0，把t=48代入即可求解．
【解答】解：因为N(t)=N0e−t24，
所以N′(t)=−124N0e−t24，
当t=48时，−N024e−2=−1，
所以N0=24e2，
则N(48)=24e2×e−2=24.
故选：C.
7.【答案】B
【解析】解：设切点M(m,n)，y′=3x2+2，
则3m2+2=5，解得m=1或−1；
若m=1，则n=5+b=13+2×1+1=4⇒b=−1；
若m=−1，则n=−5+b=(−1)3+2×(−1)+1=−2⇒b=3；
综上所述，b=−1或3，
故选：B.
设切点M(m,n)利用导数的几何意义可求得m=1或−1，继而可求得b.
本题考查利用导数研究曲线上某点的切线方程，考查函数与方程思想，考查数学运算能力等核心素养，属于中档题．
8.【答案】B
【解析】解：按照甲是否在天和核心舱划分，
①若甲在天和核心舱，天和核心舱需要从除了甲乙之外的4人中再选取1人，剩下3人去剩下两个舱位，则有C41⋅C32=12种可能；
②若甲不在天和核心舱，则在问天实验舱，剩下4人中选取3人进入天和核心舱即可，则有C43=4种可能；
根据分类加法计数原理，共有12+4=16种可能．
故选：B.
可以按照元素甲分类讨论，特殊元素和特殊位置优先考虑即可得解．
本题考查排列组合的应用，属于基础题．
9.【答案】C
【解析】解：an=11+2+3+⋯+n=2(n+1)n=2(1n−1n+1)，
∴该数列的前n项和为Sn=2(1−12+12−13+…+1n−1n+1)=2nn+1，
令2nn+1=95得n=9.
故选C.
利用等差数列的求和公式得出所给数列的通项公式，使用裂项法求和，列出方程解出n即可．
本题考查了等差数列的求和公式，裂项法求和，属于中档题．
10.【答案】C
【解析】解：设AB的中点为C，
因为|OA+OB|≥|AB|，
所以|OC|≥|AC|，
因为|OC|=|a| 2，|AC|2=4−|OC|2，
所以2(|a| 2)2≥4，
所以a≤−2或a≥2，
因为|a| 20)的渐近线为：y=±bax，即bx±ay=0，
因为右焦点F(c,0)到一条渐近线的距离为 32c，
所以bc a2+b2= 32c，
即bc= 32，
解得2b= 3c，
又a2+b2=c2，
所以4(c2−a2)=3c2⇒c2=4a2⇒c2a2=4⇒e2=4，
因为e>1，所以e=2，
故答案为：2.
根据给定条件求出双曲线的渐近线，再用点到直线的距离公式建立a，b，c的等量关系式，计算可得结果．
本题考查了双曲线的性质，重点是离心率的计算，属于基础题．
15.【答案】408
【解析】解：根据题意，分成两类情况：
①四位数中没有偶数，即在1，3，5，7中任选4个，共有A44=24种，
②四位数中只有一个偶数，即在1，3，5，7中任选3个，在2，4，6，8种选一个，共有C43C41A44=384种，
故共有24+384=408.
故答案为：408.
根据题意，分成两类情况：①四位数中没有偶数，即在1，3，5，7中任选4个，②四位数中只有一个偶数，即在1，3，5，7中任选3个，在2，4，6，8种选一个，然后结合排列组合即可求解．
本题主要考查了分类与分步计数原理，还考查了排列组合知识的应用，属于基础题．
16.【答案】 155
【解析】解：根据题意，设D到平面ABC的距离为h，连接OC，
∵△ABD为等边三角形，O为BD的中点，∴AO⊥BD，
由于AB=2，则AO= 4−1= 3，
同理：CO= 3.
又由AC= 6，
在△AOC中，∵AO2+CO2=AC2，则有∠AOC=90∘，即AO⊥OC，
又由AO⊥BD，
则有AO⊥平面BCD，
过点E作OE⊥BC，交BC与点E，连接AE，
则OE=OBsin60∘= 32，
又由AO= 3，则AE= AO2+OE2= 152，
故S△ABC=12×AE×BC=12×2× 152= 152，S△BDC= 34×22= 3，
VA−BCD=13×AO×S△BCD，VD−ABC=13hS△BCD，
∴由等体积法可得：VA−BCD=VD−ABC，即13× 3× 3=13× 152h，
变形可得：h=6 15=2 155.
∴点O到平面ABC的距离为12h= 155.
故答案为： 155.
根据题意，设D到平面ABC的距离为h，连接OC，先证AO⊥平面BCD，过O作OE⊥BC于E，连接AE，利用等体积能求出D到平面ABC的距离．从而能求出点O到平面ABC的距离．
本题考查点到平面的距离，涉及棱锥的体积公式，属于中档题．
17.【答案】43 ； (53,+∞)
【解析】解：根据题意，由余弦定理可知：a2+c2−b2=2accsB，
则S=12acsinB=13(a2+c2−b2)=13×2accsB，变形可得sinB=43csB，则tanB=43，
又由B锐角，则sinB=45，csB=35，
ca=sinCsinA=sin(A+B)sinA=sinAcsB+csAsinBsinA=csB+sinB×1tanA=45×1tanA+35，
又由A=π−(B+C)=(π−C)−B，且C为钝角，则A≤π2−B，则tanA≤tan(π2−B)=34，
则ca≥45×43+35=53，
即ca的取值范围是(53,+∞)；
故答案为：43，(53,+∞).
根据题意，对于第一空：先由余弦定理和三角形面积公式可得S=12acsinB=13(a2+c2−b2)=13×2accsB，变形可得sinB=43csB，据此可得答案；对于第二空：由正弦定理可得ca=sinCsinA=sin(A+B)sinA=sinAcsB+csAsinBsinA=csB+sinB×1tanA=45×1tanA+35，结合诱导公式分析tanA的范围，计算可得答案．
本题主要考查了余弦定理的应用．解题的过程中主要是利用了余弦定理的变形公式，把边的问题转化为角的问题．
18.【答案】①②④
【解析】【分析】
本题考查数列的求和以及和与项之间的关系，侧重考查了学生的逻辑推理和运算能力，属于难题．
对于①，利用并项法判断，对于②，利用和与项的关系判断；对于③，利用反证法推出矛盾；对于④结合不等式的性质推导．
【解答】
解：对于①，利用并项法得：Tn=(a1−a2)+(a3−a4)+⋯+(a2021−a2022)+a2023=−1011+2023=1012，故①对；
对于②，Tn=n，令bn=(−1)n+1an，则Tn=b1+b2+…+bn=n，故Tn−1=n−1，所以bn=Tn−Tn−1=1=(−1)n+1an，故an=(−1)n+1，故a2022=−1，故②对；
对于③，假设存在各项均为整数的数列{an}，使得|Tn|>|Tn+1|对任意的n∈N*都成立，则必有|T1|>|T2|>|T3|>……，且都是正整数，令|T1|=N，则必有|T2|≤N−1，|T3|≤N−2，……，|TN|≤1，|TN+1|≤0，|Tn+2|≤−1，则与|TN+2|≥0矛盾，故③错；
对于④，由已知Tn=a1−a2+a3−a4+⋯+(−1)n+1an，可知(−1)n+2an+1=Tn+1−Tn，当n≥2时，有(−1)n+1an=Tn−Tn−1，
即n≥2时，an+1=(−1)n+2(Tn+1−Tn)，an=(−1)n+1(Tn−Tn−1)，
故|an+1−an|=|(−1)n+1||Tn−Tn+1−Tn+Tn−1|=|Tn−1−Tn+1|≤|Tn−1|+|Tn+1|