



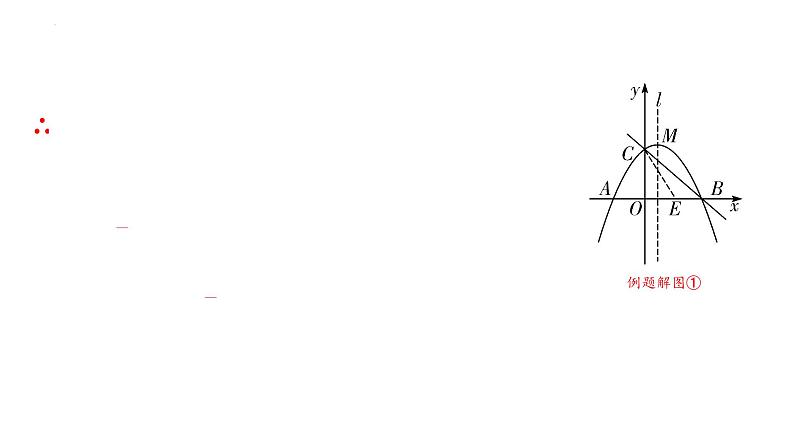

还剩41页未读,
继续阅读
中考数学二轮重点专题研究 微专题 二次函数与线段、周长问题(课件)
展开
这是一份中考数学二轮重点专题研究 微专题 二次函数与线段、周长问题(课件),共49页。PPT课件主要包含了例题图①,例题解图①,例题图⑤,例题图⑥,例题图⑧,第1题图,第3题图等内容,欢迎下载使用。
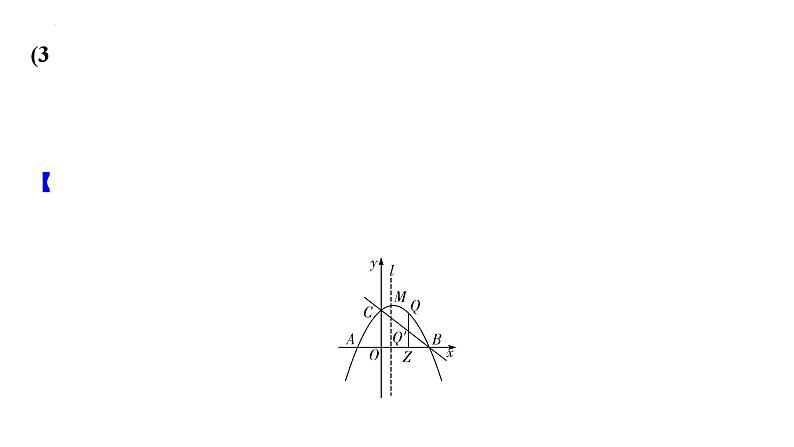
【思维教练】要求点Q到直线BC的距离,过点Q作QN⊥BC于点N,结合QQ′∥y轴及OC,OB的长度可得QN和QQ′之间的数量关系,则求出QQ′的最大值即可得到QN的最大值.
【思维教练】根据矩形的性质,可得QQ′=KF,FQ′=KQ,只需分别表示出QQ′和KQ的长,用代数式表示出矩形QKFQ′的周长,结合二次函数的性质即可求解.
【思维教练】要求△ACN周长的最小值,因为AC是定值,则求出AN+CN的最小值即可,由点A、B对称可知当点N位于直线l与BC的交点时,AN+NC=BC,即AC+BC为△ACN周长的最小值.
解:存在.如解图,连接AC,在Rt△OAC中,
【思维教练】根据点P的横坐标,表示出线段PD的长,点P到y轴的距离即P点的横坐标,根据DP与点P的横坐标相等,列等量关系求解即可.
解:如解图,延长PF交x轴于点E,
解:如解图,过点P作y轴的平行线交直线AD于点M,
解:①如解图,过点P作y轴的平行线交直线AD于点Q,
【思维教练】要求点Q到直线BC的距离,过点Q作QN⊥BC于点N,结合QQ′∥y轴及OC,OB的长度可得QN和QQ′之间的数量关系,则求出QQ′的最大值即可得到QN的最大值.
【思维教练】根据矩形的性质,可得QQ′=KF,FQ′=KQ,只需分别表示出QQ′和KQ的长,用代数式表示出矩形QKFQ′的周长,结合二次函数的性质即可求解.
【思维教练】要求△ACN周长的最小值,因为AC是定值,则求出AN+CN的最小值即可,由点A、B对称可知当点N位于直线l与BC的交点时,AN+NC=BC,即AC+BC为△ACN周长的最小值.
解:存在.如解图,连接AC,在Rt△OAC中,
【思维教练】根据点P的横坐标,表示出线段PD的长,点P到y轴的距离即P点的横坐标,根据DP与点P的横坐标相等,列等量关系求解即可.
解:如解图,延长PF交x轴于点E,
解:如解图,过点P作y轴的平行线交直线AD于点M,
解:①如解图,过点P作y轴的平行线交直线AD于点Q,












