中考数学一轮复习课件 尺规作图、视图与投影

这是一份中考数学一轮复习课件 尺规作图、视图与投影，共39页。PPT课件主要包含了尺规作图，三视图常考点，由前向后，由上向下，由左向右，长对正，高平齐，三视图易错点，平行投影和中心投影，尺规作图的应用等内容，欢迎下载使用。
1.三视图的概念(1)主视图:在正面内得到的　 　观察物体的视图. (2)俯视图:在水平面内得到的　 　观察物体的视图. (3)左视图:在侧面内得到的　 　观察物体的视图. 2.画三视图的要素画三视图时,三个视图都要放在正确的位置,并且注意主视图与俯视图的　 　,主视图与左视图的　 　,左视图与俯视图的宽相等. 
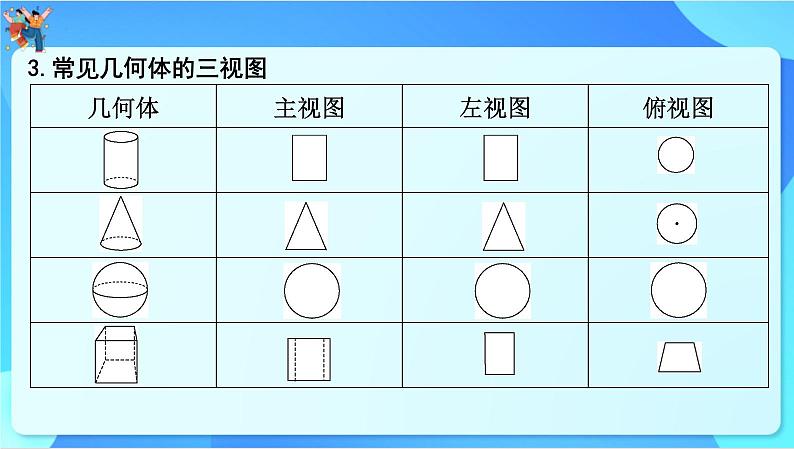
3.常见几何体的三视图
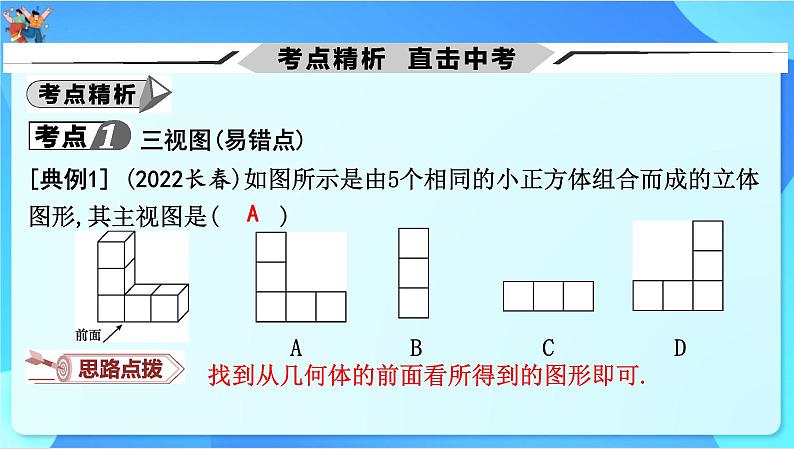
[典例1] (2022长春)如图所示是由5个相同的小正方体组合而成的立体图形,其主视图是(　 　)
找到从几何体的前面看所得到的图形即可.
A B C D
画三视图时常见错误(1)混淆三种视图,弄错视线方向;(2)漏掉部分轮廓线;(3)看不见的轮廓线画成了实线.
[变式1] (2023眉山)由相同的小正方体搭成的立体图形的部分视图如图所示,则搭成该立体图形的小正方体的最少个数为(　 　)A.6B.9C.10D.14
左视图 俯视图
由左视图和俯视图综合分析,即可得到答案.
[典例2] (2022北部湾)古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图所示,木杆EF长2米,它的影长FD是4米,同一时刻测得OA是268米,则金字塔的高度BO是　 　米. 
在同一时刻物高和影长成正比例,即在同一时刻的两个物体、影长、经过物体顶部的太阳光线构成的两个直角三角形相似.
[变式2] 小明家的客厅有一张直径为1.2 m,高0.8 m的圆桌BC,在距地面2 m的A处有一盏灯,圆桌的影子为DE,依据题意建立平面直角坐标系 (如图所示),其中点D坐标为(2,0),求点E的坐标.
根据中心投影的性质可知△ABC∽△ADE,根据相似三角形的性质得比例式,从而求得点E的坐标.
[典例3] (2022无锡)如图所示,△ABC为锐角三角形.
① ②
(1)请在图①中用无刻度的直尺和圆规作图:在AC右上方确定点D,使∠DAC=∠ACB,且CD⊥AD;(不写作法,保留作图痕迹)
(1)根据要求作出图形即可;
(2)在(1)的条件下,若∠B=60°,AB=2,BC=3,求四边形ABCD的面积.
(2)过点A作AH⊥BC于点H,求出AH,AD,利用梯形面积公式求解.
尺规作图的关键(1)掌握六种基本作图的步骤;(2)读懂题意,根据题目要求,综合运用基本作图解决问题.
[变式3] (2023济宁)如图所示,BD是矩形ABCD的对角线.(1)作线段BD的垂直平分线(要求:尺规作图,保留作图痕迹,不必写作法和证明).
解:(1)如图所示,直线MN就是线段BD的垂直平分线.
(2)设BD的垂直平分线交AD于点E,交BC于点F,连接BE,DF.①判断四边形BEDF的形状,并说明理由;
解:(2)①四边形BEDF是菱形.理由如下:由作图可知OB=OD.∵四边形ABCD是矩形,∴AD∥BC,∴∠EDO=∠FBO.∵∠EOD=∠FOB,∴△EOD≌△FOB(ASA),∴ED=FB,∴四边形BEDF是平行四边形.又∵EF是BD的垂直平分线,∴BF=DF,∴平行四边形BEDF是菱形.
②若AB=5,BC=10,求四边形BEDF的周长.
解:②∵四边形ABCD是矩形,BC=10,∴∠A=90°,AD=BC=10.由①可设BE=ED=x,则AE=10-x.∵AB=5,∴在Rt△ABE中,AB2+AE2=BE2,即25+(10-x)2=x2,解得x=6.25,∴菱形BEDF的周长为6.25×4=25.
三视图与几何体的综合计算
[典例4] 如图所示是某几何体的三视图.
(2)由圆锥的侧面积和圆锥的底面积相加得圆锥的全面积.
(1)由三视图可知该几何体为底面直径为4 cm、母线长为5 cm的圆锥;
(1)写出这个几何体的名称;(2)根据图示数据计算这个几何体的表面积.
解:(1)由此几何体的三视图知该几何体是底面直径为4 cm、母线长为5 cm的圆锥.
由三视图求几何体表面积(侧面积)或体积的三个“步骤”第一步:根据三视图确定立体图形的形状;第二步:根据三视图标注的数据计算出立体图形的相关数据;第三步:根据立体图形的表面积(侧面积)或体积的公式进行计算.
立体图形的平面展开图
[典例5] (2022绥化)下列图形中,正方体展开图错误的是(　 　)
A B C D
利用正方体及其表面展开图的特点解题.
[变式5] (2022常德)如图所示是一个正方体的展开图,将它折成正方体后,“神”字对面的字是　 　. 
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答即可.
1.(2022临沂)如图所示三棱柱的展开图不可能是(　 　)
2.(2023自贡)如图所示六棱柱的左视图是(　 　)
3.(2022泰州)如图所示为一个几何体的表面展开图,则该几何体是(　)A.三棱锥B.四棱锥C.四棱柱D.圆锥
6.(2022重庆A卷)在学习矩形的过程中,小明遇到了一个问题:在矩形ABCD中,E是AD边上的一点,试说明△BCE的面积与矩形ABCD的面积之间的关系.他的思路是:首先过点E作BC的垂线,将其转化为证明三角形全等,然后根据全等三角形的面积相等使问题得到解决.请根据小明的思路完成下面的作图与填空.
1.(2022河北)要得知作业纸上两相交直线AB,CD所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案 (如图①和图②所示):
对于方案Ⅰ,Ⅱ,说法正确的是(　 　)A.Ⅰ可行、Ⅱ不可行B.Ⅰ不可行、Ⅱ可行C.Ⅰ、Ⅱ都可行D.Ⅰ、Ⅱ都不可行