河北省保定市部分高中2024届高三下学期二模考试数学试卷(含答案)

这是一份河北省保定市部分高中2024届高三下学期二模考试数学试卷(含答案)，共15页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．双曲线的渐近线方程为( )
A.B.C.D.
2．已知,,集合,,若,则( )
A.1B.C.D.
3．下图是我国2023年3月至12月社会消费品零售总额同比增速的折线图,则这10个月社会消费品零售总额同比增速的分位数为( )
A.B.C.D.
4．设,,则( )
A.B.C.D.
5．下列函数在上单调递减的是( )
A.B.
C.D.
6．已知函数,若,则m的取值范围是( )
A.B.C.D.
7．已知抛物线的焦点为F,准线为l,过抛物线上一点A作l的垂线,垂足为B,直线交y轴于点C,若,且的面积为,则（ ）
A.1B.C.2D.
8．3名男生和3名女生随机站成一排,每名女生至少与1名男生相邻,则不同的排法种数为( )
A.198B.220C.320D.360
二、多项选择题
9．已知m,n是两条异面直线,,,是三个不同的平面,,,,,,则下列说法正确的是( )
A.B.C.,D.
10．虚数z满足,则下列说法正确的是( )
A.z的虚部为1
B.
C.z在复平面内对应的点在第二象限
D.
11．已知函数则下列说法正确的是( )
A.
B.关于x的方程有五个不同的实根,则m的取值范围为
C.函数有3个零点
D.关于x的方程的所有根之和为209
三、填空题
12．已知圆,则以为中点的弦所在直线的方程为__________.
13．非直角的内角A,B,C的对边分别为a,b,c,若,则_______________.
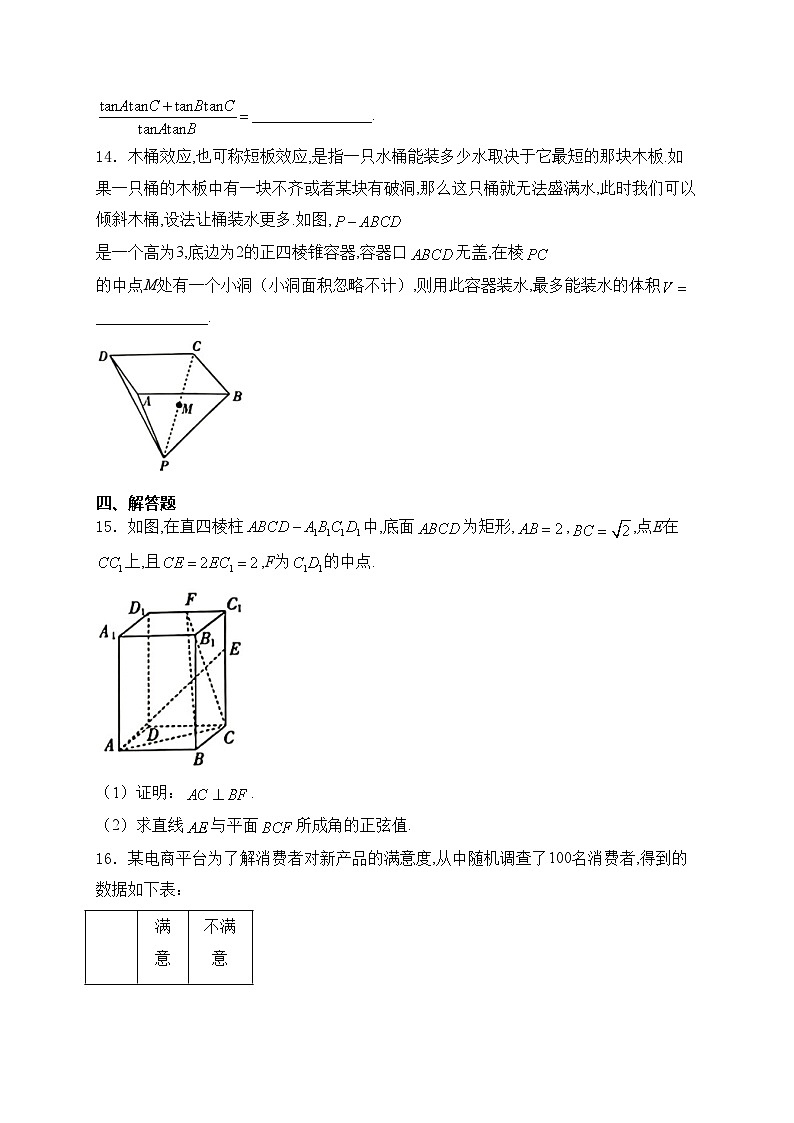
14．木桶效应,也可称短板效应,是指一只水桶能装多少水取决于它最短的那块木板.如果一只桶的木板中有一块不齐或者某块有破洞,那么这只桶就无法盛满水,此时我们可以倾斜木桶,设法让桶装水更多.如图,是一个高为3,底边为2的正四棱锥容器,容器口无盖,在棱的中点M处有一个小洞（小洞面积忽略不计）,则用此容器装水,最多能装水的体积______________.
四、解答题
15．如图,在直四棱柱中,底面为矩形,,,点E在上,且,F为的中点.
（1）证明：.
（2）求直线与平面所成角的正弦值.
16．某电商平台为了解消费者对新产品的满意度,从中随机调查了100名消费者,得到的数据如下表：
（1）根据上表,依据小概率值的独立性检验,能否据此推断消费者对新产品的满意度与性别有关？
（2）设数据在表内均匀分布,以事件发生的频率作为相应事件发生的概率.该电商平台从新产品的所有消费者中随机抽取3人,对新产品满意的客户奖励20元现金红包,对新产品不满意的客户奖励10元现金红包,用X表示现金红包的总金额,求.
附.
17．已知数列满足.
（1）求的通项公式;
（2）若求数列的前n项和.
18．已知函数,为的导函数.
（1）若是的极大值点,求a的取值范围;
（2）已知,,若存在,使得成立,证明：.
19．如果方程能确定y是x的函数,那么称用这种方式表示的函数是隐函数.隐函数的求导方法：在方程中,把看成的函数,于是方程可看成关于的恒等式,在等式两端同时对求导,解出即可.例如,求方程所确定的隐函数的导数,在方程的两端同时对x求导,则（是中间变量,需要用复合函数的求导法则）,得.已知O为坐标原点.
（1）求曲线在点处的切线方程;
（2）已知F是椭圆的左焦点,过椭圆C上一点P作椭圆C的切线,与y轴交于点M,且,,求椭圆C的离心率;
（3）已知A,B是椭圆上两个不同的点,过A,B分别作直线,与椭圆E相切,与的交点为N,若,求动点N的轨迹方程.
参考答案
1．答案：B
解析：由题可知双曲线的渐近线方程为.
2．答案：C
解析：若,,则,,不成立.
可知,,,.
解得,,故.
3．答案：D
解析：,将这10个数据从小到大排列,则第6个数为.
4．答案：A
解析：,,,所以.
5．答案：D
解析：对于A,B选项,,,结合的图象（图略）,可知A,
B选项对应的函数均不符合题意.对于C,D选项,,,
结合的图象（图略）,可知C选项对应的函数不符合题意,D选项对应的函数符合题意.
故选:D.
6．答案：A
解析：由题可知的定义域为,,
所以在上单调递增,由,可得,
即,故m的取值范围是.
7．答案：B
解析：由题可知,又,所以,不妨设点A位于第一象限,则.
由抛物线的定义得,所以,则.
故的面积为,解得.
8．答案：D
解析：当恰好2名女生相邻时,有种排法,当3名女生都不相邻时,有144种排法,则共有种排法.
9．答案：CD
解析：A,B选项无法确定.因为,,,,
所以,,C选项正确.由题可知,,且m,n是两条异面直线,则,D选项正确.
10．答案：AC
解析：由,可得,所以虚数.故z的虚部为1,,z在复平面内对应的点在第二象限.又,所以.
故选：AC.
11．答案：ACD
解析：的部分图象如图所示,由题可知,,
所以,故A正确.
关于x的方程有五个不同的实根,则m的取值范围为,故B错误.
的零点个数可转化为与图象的交点个数,的图象经过点,又当时,,当时,,所以与的图象有3个交点,故C正确.
因为的图象关于直线对称,所以关于x的方程的所有根之和为,故D正确.
12．答案：
解析：由圆的方程可知圆心坐标为,则,则所求直线的斜率1,直线方程为,即.
13．答案：1
解析：由,可得,
又,
所以
.
14．答案：
解析：经过的平面与线段,交于点E,F,如图1,
连接,,则最多能装水的体积为四棱锥的体积的最大值.
将四棱锥倒转,连接,与交于点H,连接,与交于点G.
易知G为,的重心,,,E,G,F三点
共线,注意到,平面.
故.
如图2,,
,,
且.故,即.
令,于是在上的值域为,
则的值域为,因此,所求的最大值为.
15．答案：（1）见解析
（2）
解析：（1）证明：取G为的中点,连接,,
因为,,所以,
则,
又,所以,即.
因为F,G分别为,的中点,所以,
因为平面,所以平面,则.
因为,所以平面,
因为平面,所以.
（2）以D为坐标原点,分别以向量,,的方向为x轴､y轴､z轴的正方向,
建立如图所示的空间直角坐标系,
所以,,,,,
,,,
设平面的法向量为,
则即
令,则,,所以.
设直线与平面所成的角为,
则,
所以直线与平面所成角的正弦值为.
16．答案：（1）认为消费者对新产品的满意度与性别有关
（2）54
解析：（1）零假设：消费者对新产品的满意度与性别无关.
,
根据小概率值的独立性检验,推断不成立,
即认为消费者对新产品的满意度与性别有关.
（2）由表可知消费者对新产品的满意的概率为0.8,
设Y表示随机抽取的3人中对新产品满意的人数,则,
所以.
又,
所以.
17．答案：（1）
（2）
解析：（1）当时,,解得.
当时,,
则,
两式相减,得,化简可得,
又因为,所以数列是以2为首项,2为公比的等比数列,
故,即.
（2）.
当n为偶数时,令,
则,
当n为奇数时,
.
故
18．答案：（1）
（2）见解析
解析：（1）.
因为是的极大值点,所以,即,
所以.
当时,,此时是的极大值点,符合题意.
当时,令,可得或,
因为是的极大值点,所以,解得.
综上,a的取值范围为.
（2）证明：不妨设,因为,
所以,
即,所以.
由,得,
则,
即,
所以.
设,构造函数,
则,
所以在上为增函数,所以,
即,又,所以.
19．答案：（1）
（2）
解析：（1）对两边取对数,得,
两边求导可得,,
代入,可得,
故曲线在点处的切线方程为,
即.
（2）设点,,则,对两边求导,
可得,
将代入,可得,
故椭圆C在点P处的切线方程为,,即.
令,可得,即.
,
.
,
,
故椭圆C的离心率为:.
（3）设,,由（2）可知,椭圆E在点A,B处的切线方程分别为,,则,,
所以直线的方程为.
将直线的方程与椭圆E的方程联立,
即可得,
,,
,,
因为,所以,解得,
化简可得,故动点N的轨迹方程为.
满意
不满意
男生
30
13
女生
50
7
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828