北师大版九年级上册4 探索三角形相似的条件课文ppt课件

这是一份北师大版九年级上册4 探索三角形相似的条件课文ppt课件，共12页。PPT课件主要包含了分别相等，成比例，△AEB，△DOE等内容，欢迎下载使用。
1. 相似三角形的定义：三角 、三边 的两个三角形叫做相似三角形.2. 相似三角形的判定定理1：两角 的两个三角形相似.
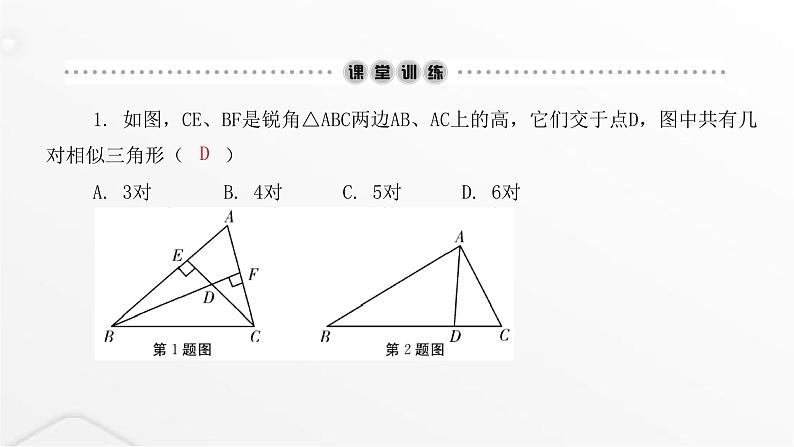
1. 如图，CE、BF是锐角△ABC两边AB、AC上的高，它们交于点D，图中共有几对相似三角形（）A. 3对B. 4对C. 5对D. 6对
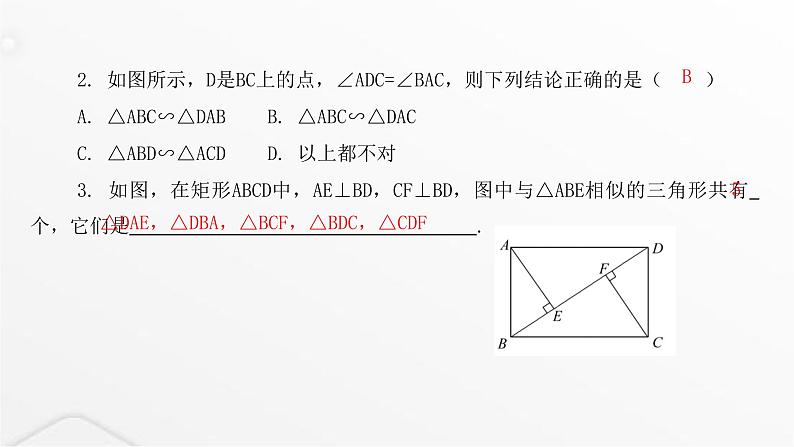
2. 如图所示，D是BC上的点，∠ADC=∠BAC，则下列结论正确的是（ ）A. △ABC∽△DABB. △ABC∽△DACC. △ABD∽△ACDD. 以上都不对3. 如图，在矩形ABCD中，AE⊥BD，CF⊥BD，图中与△ABE相似的三角形共有 个，它们是 .
△DAE，△DBA，△BCF，△BDC，△CDF
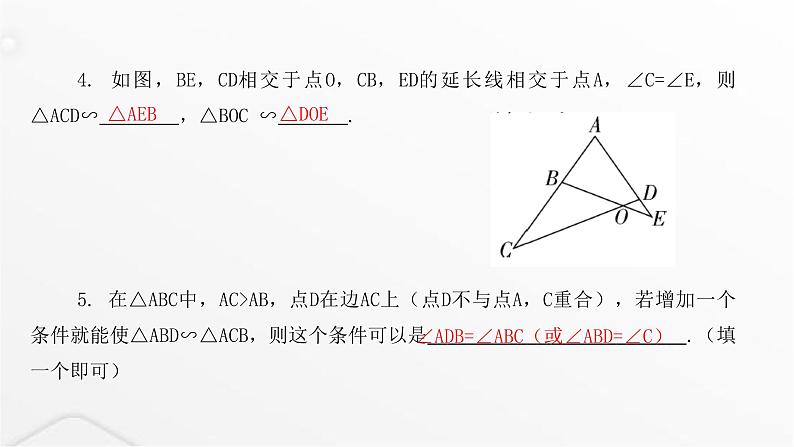
4. 如图，BE，CD相交于点O，CB，ED的延长线相交于点A，∠C=∠E，则△ACD∽ ，△BOC ∽ .5. 在△ABC中，AC>AB，点D在边AC上（点D不与点A，C重合），若增加一个条件就能使△ABD∽△ACB，则这个条件可以是 .（填一个即可）
∠ADB=∠ABC（或∠ABD=∠C）
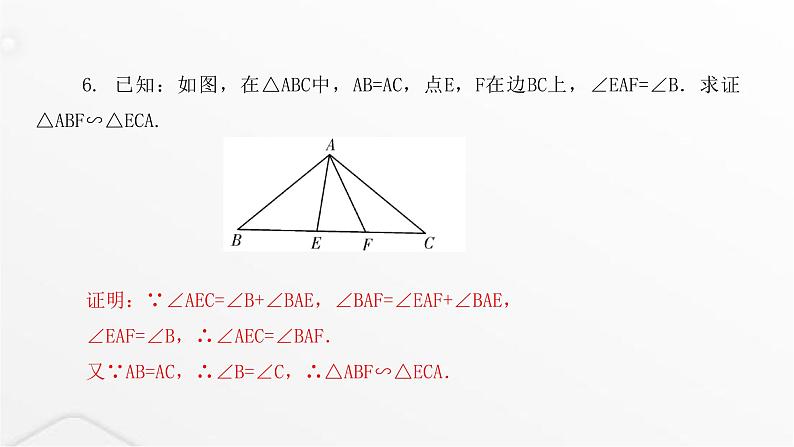
6. 已知：如图，在△ABC中，AB=AC，点E，F在边BC上，∠EAF=∠B．求证△ABF∽△ECA.
证明：∵∠AEC=∠B+∠BAE，∠BAF=∠EAF+∠BAE，∠EAF=∠B，∴∠AEC=∠BAF．又∵AB=AC，∴∠B=∠C，∴△ABF∽△ECA．
【基础训练】1. 下列各组图形中，不一定相似的是（ ）A. 各有一个角是100°的两个等腰三角形B. 各有一个角是90°的两个等腰三角形C. 各有一个角是60°的两个等腰三角形D. 各有一个角是50°的两个等腰三角形2. 如图，在△ABC中，点D，E分别在边AB，AC上，如果DE∥BC，且∠DCE=∠B，那么下列说法中，错误的是( )A. △ADE∽△ABCB. △ADE∽△ACDC. △ADE∽△DCBD. △DEC∽△CDB
3. 如图，在Rt△ABC中，CD是斜边AB上的高，DE，DF分别是△ACD和△BCD的中线，则图中一定相似的三角形共有（）A. 3对B. 4对C. 5对D. 6对4. 如图，点P是等腰梯形ABCD的底AD上的一点，若∠A=∠BPC，则和△ABP相似的三角形有 个．
5. 如图，已知AB∥CD，AO＝9，AC＝12，BD＝36，求OD的长.
【提升训练】6. 如图，若添上一个条件： ，则△ABC∽△ADE.
∠ABC=∠D（或∠ACB=∠E或BC∥DE）
7. 如图，∠1=∠3，∠B=∠D，AB=DE=5，BC=4.(1)△ABC与△ADE相似吗？请说明理由.(2)求AD的长.
8. 如图，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D．（1）求证：△BAD∽△CAD；（2）若O是AC边上一点，连接BO交AD于点E，OF⊥OB交BC边于点F，求证：△ABE∽△COF．
证明：（1）∵AD⊥BC，∴∠ADB=∠CDA=90°，∠DAC+∠C=90°，∵∠BAC=90°，∴∠B+∠C=90°，∵∠DAC=∠B，∴△BAD∽△ACD.（2）由（1）知，∠BAE=∠C，∵OF⊥OB，∴∠BOA+∠COF=90°，∵∠BOA+∠ABE=90°，∴∠ABE=∠COF，∴△ABE∽△COF．