数学八年级上册第一章 勾股定理1 探索勾股定理图文课件ppt

这是一份数学八年级上册第一章 勾股定理1 探索勾股定理图文课件ppt，共10页。PPT课件主要包含了平方和，a2+b2c2，125cm2，251cm2等内容，欢迎下载使用。

1. 勾股定理：直角三角形两直角边的 等于斜边的 .如果用a，b和c分别表示直角三角形的两直角边和斜边，那么 .2. 我国历史上将弦上的正方形称为弦图（如图）.
1. 已知一个等边三角形的边长为6 cm，则以它的高为边长的正方形的面积为()A. 36 cm2B. 27 cm2C. 18 cm2D. 12 cm22. 一个直角三角形的两条边的长分别是9和40，则第三条边的长的平方是（）A. 1 681B. 1 781C. 1 519或1 681D. 1 5193. 一个直角三角形三条边的长为三个连续的自然数，则这三条边的长分别为 ．
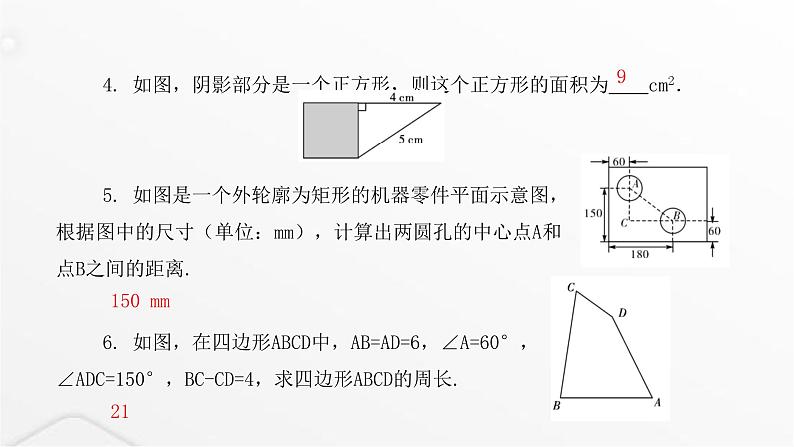
4. 如图，阴影部分是一个正方形，则这个正方形的面积为 cm2．5. 如图是一个外轮廓为矩形的机器零件平面示意图，根据图中的尺寸（单位：mm），计算出两圆孔的中心点A和点B之间的距离.6. 如图，在四边形ABCD中，AB=AD=6，∠A=60°，∠ADC=150°，BC-CD=4，求四边形ABCD的周长.
【基础训练】1. 如图，在△ABC中，CE平分∠ACB，CF平分△ABC的外角∠ACD，且EF∥BC交AC于M，若CM=4，则CE2+CF2的值为( )A.8B.16C.32D.642. 已知Rt△ABC的两直角边分别是6 cm，8 cm，则Rt△ABC斜边上的高是（ ）A. 4.8cmC.48cmD.10cm
3. 如图，一个长方体盒子的长、宽、高分别为6 cm、5 cm、3 cm，有一只甲虫从顶点A沿盒的表面爬到顶点B处，那么它所爬行的最短路线的长是 cm．
4. 如图所示是由4个全等的直角三角形构成的正方形ABCD，其面积为49 cm2，若AF=4 cm，则正方形EFGH的面积为 cm2.
【提升训练】5. 求阴影部分的面积：（1）阴影部分是正方形；（2）阴影部分是长方形.
6. 如图，小李准备建一个蔬菜大棚，棚宽4m，高3m，长20m，棚的斜面用塑料薄膜遮盖，不计墙的厚度，请计算阳光透过的最大面积.
解：在Rt△ABC中，由勾股定理，得AB2=AC2+BC2=32+42=52，即AB=5 m.所以矩形塑料薄膜的面积是5×20=100（m2）.故阳光透过的最大面积是100m2.