2024届高考数学学业水平测试复习专题七第27讲空间直线平面的垂直课件

这是一份2024届高考数学学业水平测试复习专题七第27讲空间直线平面的垂直课件，共27页。PPT课件主要包含了续上表等内容，欢迎下载使用。

第27讲　空间直线、平面的垂直1．直线与直线垂直(1)已知两条异面直线a，b，经过空间任一点O分别作直线a′∥a，b′∥b，我们把直线a′与b′所成的角叫做异面直线a与b所成的角(或夹角)．(2)如果两条异面直线所成的角是直角，那么我们就说这两条异面直线互相垂直．记作a⊥b.(3)当两条直线a，b相互平行时，我们规定它们所成的角为0°.所以空间两条直线所成角α的取值范围是0°≤α≤90°.
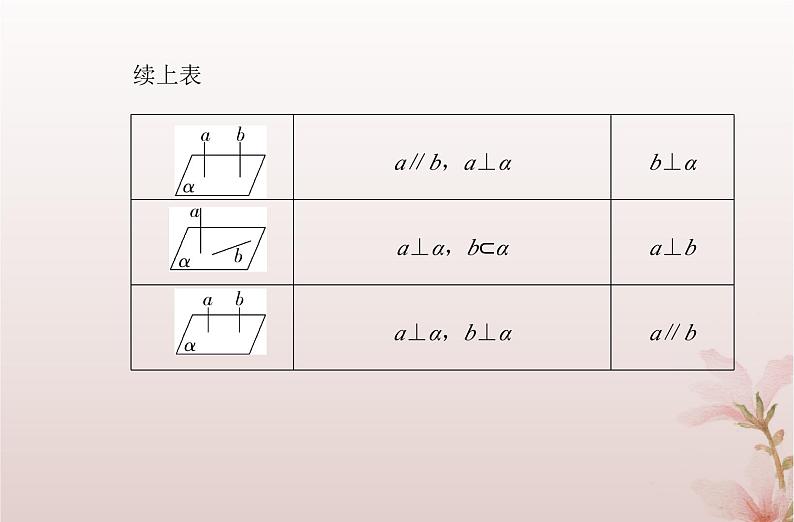
2．直线与平面垂直(1)直线与平面的定义和所成的角．①平面的一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角．②当直线与平面垂直和平行(或直线在平面内)时，规定直线和平面所成的角分别为90°和0°.(2)判定与性质．
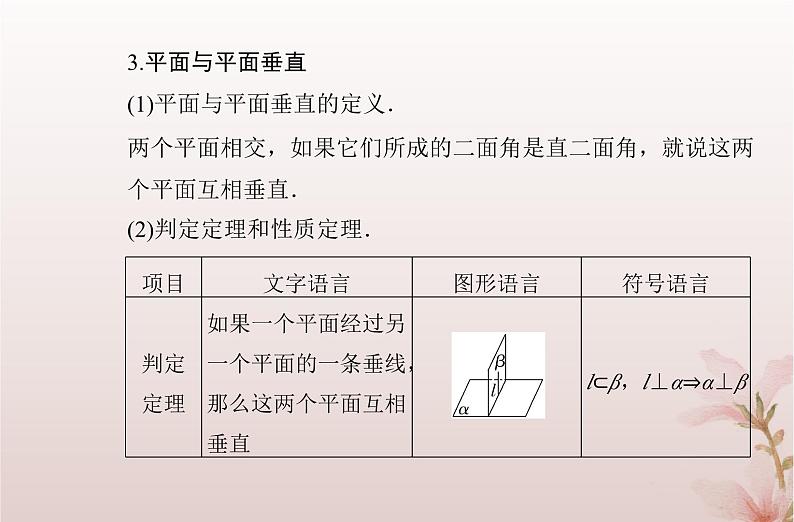
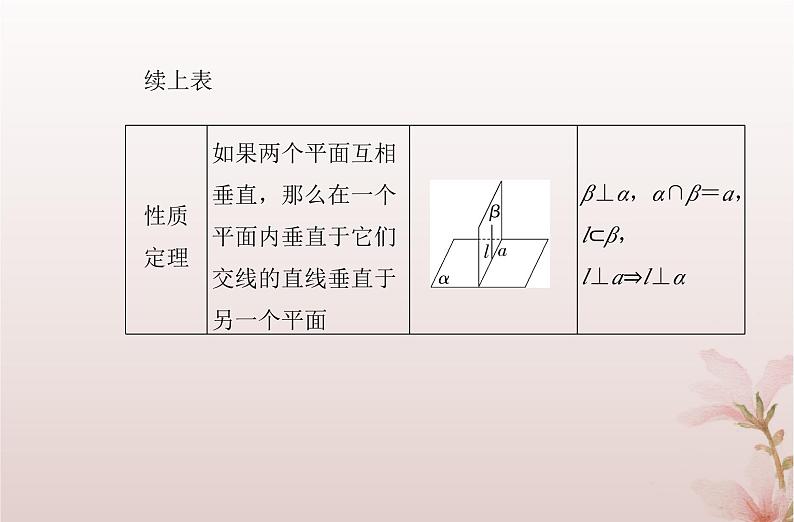
3.平面与平面垂直(1)平面与平面垂直的定义．两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直．(2)判定定理和性质定理．
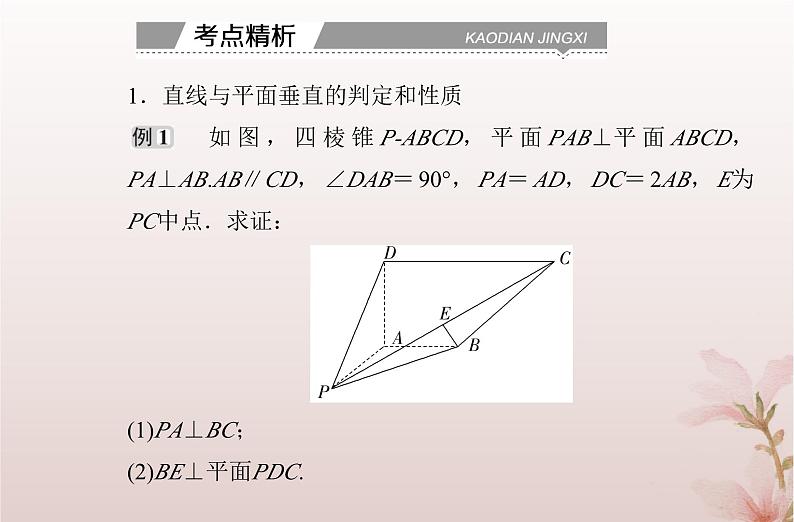
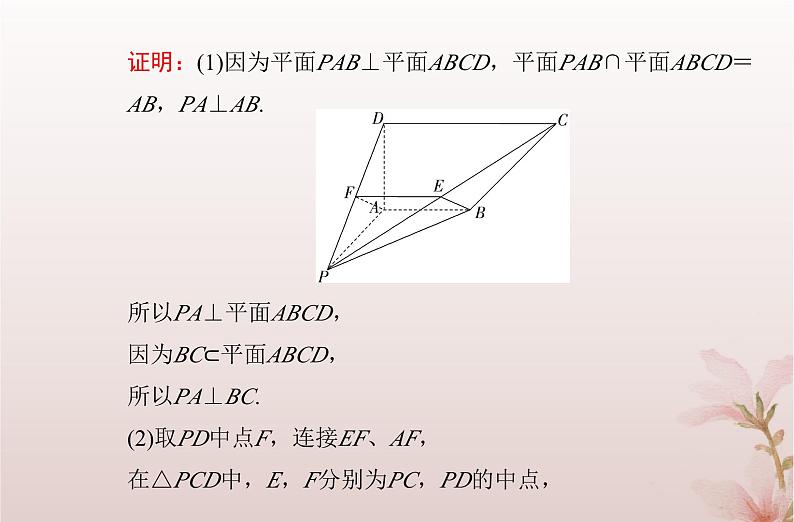
1．直线与平面垂直的判定和性质 如图，四棱锥P-ABCD，平面PAB⊥平面ABCD，PA⊥AB.AB∥CD，∠DAB＝90°，PA＝AD，DC＝2AB，E为PC中点．求证：(1)PA⊥BC；(2)BE⊥平面PDC.
证明：(1)因为平面PAB⊥平面ABCD，平面PAB∩平面ABCD＝AB，PA⊥AB.所以PA⊥平面ABCD，因为BC⊂平面ABCD，所以PA⊥BC.(2)取PD中点F，连接EF、AF，在△PCD中，E，F分别为PC，PD的中点，
所以四边形ABEF是平行四边形，所以BE∥AF，因为AP＝AD，F为PD的中点，所以AF⊥PD，所以BE⊥PD，因为PA⊥平面ABCD，DC⊂平面ABCD，所以PA⊥DC，因为AB∥CD，∠DAB＝90°，所以AD⊥DC，因为DC⊥AD，DC⊥PA，AD∩PA＝A，所以DC⊥平面PAD，
因为AF⊂平面PAD，所以DC⊥AF，因为BE∥AF，所以DC⊥BE，因为BE⊥DC，BE⊥PD，DC∩PD＝D，所以BE⊥平面PDC.
剖析：(1)证明直线和平面垂直的常用方法：①利用判定定理；②利用垂直于平面的传递性(a∥b，a⊥α⇒b⊥α)；③利用面面平行的性质(a⊥α，α∥β⇒a⊥β)；④利用面面垂直的性质．(2)证明线面垂直的核心是证明线线垂直，而证明线线垂直则需借助线面垂直的性质．因此，判定定理与性质定理的合理转化是证明线面垂直的基本思想．(3)线面垂直的性质，常用来证明线线垂直．
2．平面与平面垂直的判定与性质 如图，在四棱锥P-ABCD中，底面ABCD是矩形，点E、F分别是棱PC和PD的中点．(1)求证：EF∥平面PAB；(2)若AP＝AD，平面PAD⊥平面ABCD，求证：平面PAD⊥平面PCD.
证明：(1)因为底面ABCD是矩形，所以AB∥CD，因为点E、F分别是棱PC和PD的中点，所以EF∥CD，所以AB∥EF，又AB⊂平面PAB，EF⊄平面PAB，所以EF∥平面PAB.(2)因为AP＝AD，且F为PD的中点，所以AF⊥PD，又平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，CD⊥AD，所以CD⊥平面PAD，所以CD⊥AF，
因为PD∩CD＝D，PD、CD⊂平面PCD，所以AF⊥平面PCD，因为AF⊂平面PAD，所以平面PAD⊥平面PCD.
剖析：(1)证明平面和平面垂直的方法：①利用面面垂直的定义；②利用面面垂直的判定定理．(2)已知两平面垂直时，一般要用性质定理进行转化，在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直．
1．(2023·广东模拟)如图，在正方体ABCD-A1B1C1D1中，下列判断正确的是(　　)A．A1D⊥CC1　　　　B．BD1⊥ADC．A1D⊥AC D．AC⊥BD1D　对于A选项，因为CC1∥DD1，而∠A1DD1＝45°，则CC1与A1D所成的角为45°，故A1D与CC1不垂直，A错误；
对于B选项，连接A1B，因为A1D1⊥平面AA1B1B，A1B⊂平面AA1B1B，所以A1D1⊥A1B，所以，∠A1D1B为锐角，因为AD∥A1D1，故AD与BD1所成角不是直角，B错误；对于C选项，连接A1C1、C1D，因为AA1∥CC1且AA1＝CC1，故四边形AA1C1C为平行四边形，故A1D、AC所成角为∠C1A1D或其补角，
因为BD⊂DD1＝D，BD、DD1⊂平面BDD1，所以AC⊥平面BDD1，因为BD1⊂平面BDD1，所以AC⊥BD1，D正确．故选D.
2．若l，m为两条不同的直线，α为平面，且l⊥α，则“m∥α”是“m⊥l”的(　　)A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件A　由l⊥α且m∥α能推出m⊥l，充分性成立；若l⊥α且m⊥l，则m∥α或者m⊂α，必要性不成立，因此“m∥α”是“m⊥l”的充分不必要条件．故选A.
3．如图所示，在正方体ABCD-A1B1C1D1中，点O，M，N分别是线段BD，DD1，D1C1的中点，则直线OM与AC，MN的位置关系是(　　)A．与AC，MN均垂直B．与AC垂直，与MN不垂直C．与AC不垂直，与MN垂直D．与AC，MN均不垂直
4．(2023·广东模拟)如图所示，在正方体ABCD-A1B1C1D1中，下列直线与B1D1垂直的是(　　)A．BC1 B．A1DC．AC D．BC
C　由平行关系可确定B1D1的垂线即为BD的垂线，由此可确定结果．因为四边形ABCD为正方形，所以AC⊥BD，因为B1D1∥BD，所以AC⊥B1D1.故选C.
5．(2023·广东模拟)已知互相垂直的平面α，β交于直线l.若直线m，n满足m∥α，n⊥β，则(　　)A．m∥l B．m∥nC．n⊥l D．m⊥nC　由题意知α∩β＝l，所以l⊂β，因为n⊥β，所以n⊥l.故选C.
6．如图，已知PA⊥平面ABC，BC⊥AC，则图中直角三角形的个数为________． 解析：因为PA⊥平面ABC，AB，AC，BC⊂平面ABC，所以PA⊥AB，PA⊥AC，PA⊥BC，则△PAB，△PAC为直角三角形．由BC⊥AC，且AC∩PA＝A，得BC⊥平面PAC，从而BC⊥PC，因此△ABC，△PBC也是直角三角形．答案：4
7．(2023·广东模拟)如图，在底面是矩形的四棱锥P-ABCD中，PA⊥底面ABCD，E，F分别是PC，PD的中点．(1)若PA＝AB＝1，BC＝2，求四棱锥P-ABCD的体积；(2)求证：EF⊥平面PAD.
(2)证明：因为四边形ABCD为矩形，所以CD⊥AD，因为PA⊥底面ABCD，CD⊂面ABCD，所以PA⊥CD，又AD∩PA＝A，所以CD⊥面PAD，又E，F分别是PC，PD的中点，所以EF∥CD，所以EF⊥平面PAD.
8．(2023·广东模拟)如图，在四棱锥P­ABCD中，四边形ABCD为平行四边形，AC，BD相交于点O，点E为PC的中点，OP＝OC，PA⊥PD.求证：(1)直线PA∥平面BDE；(2)平面BDE⊥平面PCD.证明：(1)如图，连接OE，因为O为平行四边形ABCD对角线的交点，所以O为AC的中点．