2024届高考数学学业水平测试复习专题七第24讲简单几何体的表面积和体积课件

这是一份2024届高考数学学业水平测试复习专题七第24讲简单几何体的表面积和体积课件，共27页。PPT课件主要包含了答案24，答案20等内容，欢迎下载使用。

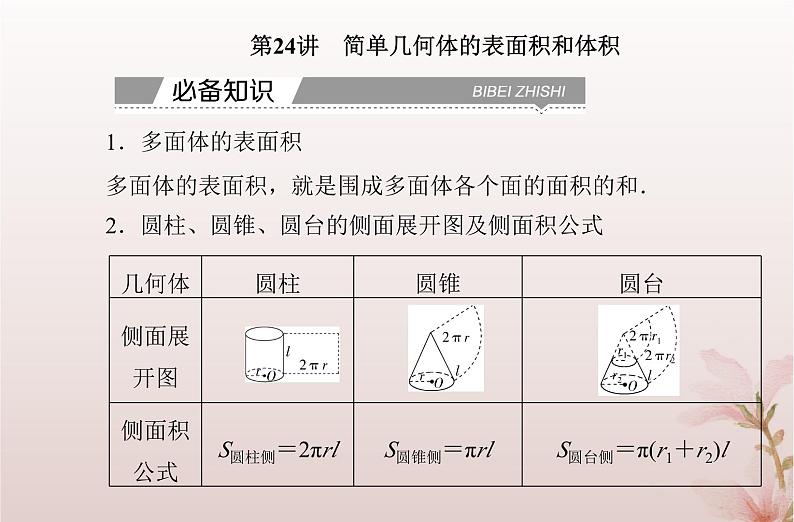
第24讲　简单几何体的表面积和体积1．多面体的表面积多面体的表面积，就是围成多面体各个面的面积的和．2．圆柱、圆锥、圆台的侧面展开图及侧面积公式
3.柱、锥、台和球的表面积和体积
4.常用结论(1)与体积有关的几个结论．①一个组合体的体积等于它的各部分体积的和或差．②底面面积及高都相等的两个同类几何体的体积相等．(2)几个与球有关的切、接常用结论．①正方体的棱长为a，球的半径为R，
剖析：空间几何体表面积的求法(1)多面体的表面积是各个面的面积之和；组合体的表面积注意衔接部分的处理．(2)旋转体的表面积问题注意其侧面展开图的应用．
剖析：空间几何体体积问题的常见类型及解题策略(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体，则可直接利用公式进行求解．(2)若所给定的几何体的体积不能直接利用公式得出，则常用转换法、分割法、补形法等方法进行求解．
3．与球有关的切、接问题 (1)正方体的内切球和外接球的表面积之比为(　　)A．3∶1　　　　　　　B．3∶4C．4∶3 D．1∶3
答案：(1)D　(2)B
剖析：空间几何体与球接、切问题的求解方法(1)求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．(2)若球面上四点P，A，B，C构成的三条线段PA，PB，PC两两互相垂直，且PA＝a，PB＝b，PC＝c，一般把有关元素“补形”成为一个球内接长方体，利用4R2＝a2＋b2＋c2求解．
B　S表＝πr2＋πrl＝πr2＋πr·2r＝3πr2＝12π，所以r2＝4，所以r＝2.故选B.
A　设圆锥的顶点为O，以母线OP为轴可作出圆锥侧面展开图如下图所示，
5．(2023·湛江统考二模)如图，将一个圆柱2n(n∈N*)等分切割，再将其重新组合成一个与圆柱等底等高的几何体，n越大，重新组合成的几何体就越接近一个“长方体”．若新几何体的表面积比原圆柱的表面积增加了10，则圆柱的侧面积为(　　)A．10π B．20πC．10nπ D．18π
A　显然新几何体的表面积比原几何体的表面积多了原几何体的轴截面面积，设圆柱的底面半径为r，高为h，则2rh＝10，所以圆柱的侧面积为2πrh＝10π.故选A.
6．如图，底面为菱形的直棱柱ABCD-A1B1C1D1的两个对角面ACC1A1和BDD1B1的面积分别为6和8，则棱柱的侧面积为____．
8.(2023·广东模拟)如图所示，三棱锥P-ABC中，PA⊥平面ABC，AB⊥AC，且E，F分别为BC，PC的中点．已知AB＝AC＝4，PA＝6，求三棱锥F-AEC的体积．
解：过F作FG∥PA交AC于G，如下图示：因为PA⊥平面ABC，所以FG⊥平面ABC，即FG是三棱锥F-AEC的高，又F为PC的中点，