2024届高考数学学业水平测试复习专题七第23讲基本立体图形立体图形的直观图课件

这是一份2024届高考数学学业水平测试复习专题七第23讲基本立体图形立体图形的直观图课件，共28页。

第23讲　基本立体图形、立体图形的直观图1．空间几何体的结构特征(1)多面体．①棱柱的侧棱都平行且相等，上、下底面是全等的多边形．②棱锥的底面是任意多边形，侧面是有一个公共顶点的三角形．③棱台可由平行于底面的平面截棱锥得到，其上、下底面是相似多边形．(2)旋转体．①圆柱可以由矩形绕其一边所在直线旋转得到．②圆锥可以由直角三角形绕其直角边所在直线旋转得到．
③圆台可以由直角梯形绕直角腰所在直线或等腰梯形绕上、下底中点连线所在直线旋转得到，也可由平行于底面的平面截圆锥得到．④球可以由半圆或圆绕直径所在直线旋转得到．2．空间几何体的直观图画空间几何体的直观图常用斜二测画法，其规则是：(1)原图形中x轴、y轴、z轴两两垂直，直观图中，x′轴、y′轴的夹角为45°(或135°)，z′轴与x′轴、y′轴所在平面垂直．(2)原图形中平行于坐标轴的线段，直观图中仍分别平行于坐标轴．平行于x轴和z轴的线段在直观图中保持原长度不变，平行于y轴的线段长度在直观图中变为原来的一半．
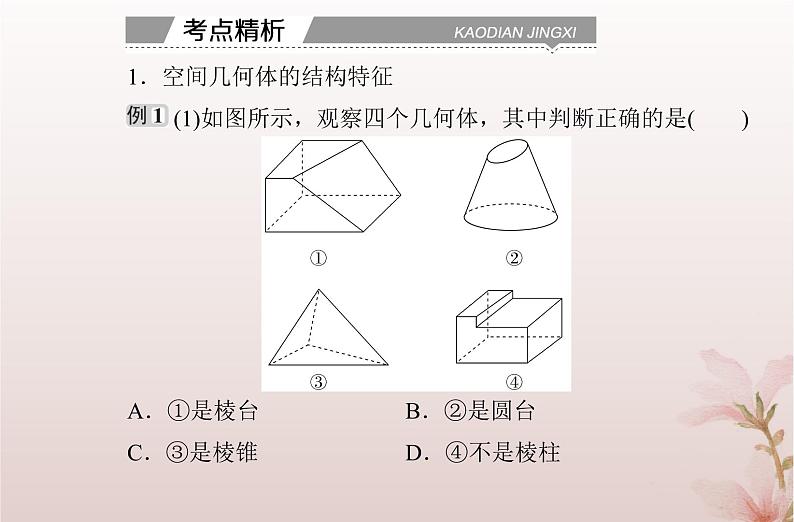
1．空间几何体的结构特征 (1)如图所示，观察四个几何体，其中判断正确的是(　　)A．①是棱台　　　　B．②是圆台C．③是棱锥 D．④不是棱柱
(2)(2023·武汉第一中学校联考期中)下列说法正确的是(　　)A．各侧面都是正方形的四棱柱一定是正方体B．球的直径是连接球面上两点并且经过球心的线段C．以直角三角形的一边所在直线为轴旋转一周所得的旋转体是圆锥D．用一个平面截圆锥，得到一个圆锥和圆台解析：(1)对于A，不是由棱锥截来的，所以①不是棱台，故A错误；对于B，上、下两个面不平行，所以②不是圆台，故B错误；对于C，底面是三角形，其余各面是有一个公共顶点的三角形，所以③是棱锥，故C正确；
对于D，前、后两个面平行，其他面是平行四边形，且每相邻两个四边形的公共边平行，所以④是棱柱，故D错误．故选C.(2)对于A：虽然各侧面都是正方形，但底面不一定是正方形，所以该四棱柱不一定是正方体，故A错误；对于B：球的直径的定义为“连接球面上两点并且经过球心的线段”，故B正确；对于C：以直角三角形的直角边所在直线为轴旋转一周所得的旋转体是圆锥，以直角三角形的斜边所在直线为轴旋转一周所得的旋转体是两个共底面的圆锥组成的几何体，故C错误；
对于D：用一个平行于底面的平面截圆锥，得到一个圆锥和圆台，故D错误．故选B.答案：(1)C　(2)B
剖析：(1)解决本类题目的关键是准确理解几何体的定义，真正把握几何体的结构特征，可以根据条件构建几何模型，在几何模型中进行判断．(2)解决本类题目的技巧：三棱柱、四棱柱、三棱锥、四棱锥是常用的几何模型，有些问题可以利用它们举特例解决或者学会利用反例对概念类的命题进行辨析．
2．空间几何体的直观图 (1)如图，用斜二测画法画一个水平放置的平面图形是一个边长为1的正方形，则原图形的形状是(　　)
(2)(2023·洛阳高一统考期中)如图，用斜二侧画法得到△ABC的直观图为等腰Rt△A′B′C′，其中A′B′＝1，则△ABC的面积为(　　)
答案：(1)A　(2)C
剖析：用斜二测画法画直观图的技巧在原图形中与x轴或y轴平行的线段在直观图中与x′轴或y′轴平行，原图中不与坐标轴平行的直线段可以先画出线段的端点再连线，原图中的曲线段可以通过取一些关键点，作出在直观图中的相应点后，用平滑的曲线连接而画出．
1．下列说法正确的有(　　)①棱台的各条侧棱所在的直线交于同一点②经过球面上不同的两点只能作一个面积最大的截面圆③各侧面都是正方形的四棱柱一定是正四棱柱④正三棱锥的各个侧面一定是全等的正三角形A．1个 B．2个C．3个 D．4个A　对于①：因为棱台是用平行于棱锥底面的平面截棱锥得到的，故延长一个棱台的各条侧棱，它们相交于一点，①正确；对于②：如果这两点是球的直径上的2个点，经过球面上的这两点作无数个面积最大的截面圆，故②错误；
对于③：各侧面都是正方形的四棱柱，如果底面是菱形，一定不是正方体，故③错误；对于④：若一个三棱锥是正三棱锥，则底面是正三角形，三个侧面是全等的等腰三角形，故④错误．所以正确的只有一个，故选A.
3．如图，边长为1的正方形O′A′B′C′是一个水平放置的平面图形OABC的直观图，则平面图形OABC以OA为轴旋转一周所围成的几何体是(　　)A．一个圆柱B．一个圆柱和一个同底面的圆锥的组合体C．两个同底的圆锥的组合体D．一个圆锥和一个同底面的圆柱(内部挖去一个同底等高的圆锥)的组合体
D　由直观图O′A′B′C′画出原图OABC，如下图所示：
4．如图，一个水平放置的平面图形的直观图是一个底角为45°的等腰梯形，已知直观图OA′B′C′的面积为4，则该平面图形的面积为(　　)
5．(2023·平顶山叶县高级中学校考高一期中)如图，△A′O′B′表示水平放置的△AOB的直观图．点B′在x′轴上，A′O′和x′轴垂直，且A′O′＝2，则△AOB的边OB上的高为(　　)
6．(2023·全国高一专题练习)下列说法正确的是________(填序号)．①以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台；②圆柱、圆锥、圆台的底面都是圆；③以等腰三角形的底边上的高线所在的直线为旋转轴，其余各边旋转一周形成的曲面所围成的几何体是圆锥；④用一个平面去截球，得到的截面是一个圆面．解析：对于①，以直角梯形直角腰所在直线为轴旋转一周可得到圆台，以直角梯形的斜腰所在直线为轴旋转一周所得的旋转体不是圆台，①错；
对于②，圆柱、圆锥、圆台的底面都是圆面，②错；对于③，以等腰三角形的底边上的高线所在的直线为旋转轴，其余各边旋转一周形成的曲面所围成的几何体是圆锥，③对；对于④，用一个平面去截球，得到的截面是一个圆面，④对．故答案为③④.答案：③④
7．如图，△A′B′C′是△ABC的直观图(斜二测画法)，其中A′与O′重合，C′在y′轴上，且B′C′∥x′轴，A′C′＝2，B′C′＝3，则△ABC的最长边长为________．
解析：由斜二测画法可知△ABC是直角三角形，且AC＝2A′C′＝4，BC＝B′C′＝3，则最长边(斜边)AB＝5.答案：5
8．已知正四棱台两底面边长分别为2和4，若侧棱与底面所成的角为45°.求：(1)棱台的高；(2)棱台的表面积．
解：(1)如图，设O1、O分别为上、下底面的中心，过C1作C1E⊥AC于E，