
2024年河北省邯郸市经开区中考一模数学试题
展开2.答题前,考生务必将姓名、准考证号填写在试卷和答题卡的相应位置.
3.所有答案均在答题卡上作答,在本试卷或草稿纸上作答无效.答题前,请仔细阅读答题卡上的“注意事项”,按照“注意事项”的规定答题.
4.答选择题时,用2B铅笔将答题卡上对应题目的答案标号涂黑;答非选择题时,请在答题卡上对应题目的答题区域内答题.
5.考试结束时,请将本试卷和答题卡一并交回.
一、选择题(本大题共16个小题,共38分.1~6小题各3分,7~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 有理数的相反数是( )
A. B. C. D.
【答案】A
【解析】
【分析】根据互为相反数的定义进行解答即可.
【详解】解:有理数的相反数是,
故选A
【点睛】本题考查的是相反数,仅仅只有符号不同的两个数互为相反数,熟记定义是解本题的关键.
2. 古典园林中的花窗通常利用对称构图,体现对称美.下面四个花窗图案,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
【答案】C
【解析】
【分析】根据中心对称图形和轴对称图形定义进行解答即可.
【详解】解:A、是轴对称图形,不是中心对称图形,故此选项不符合题意;
B、既不是轴对称图形,也不是中心对称图形,故此选项不合题意; 该试卷源自 每日更新,享更低价下载。C、既轴对称图形,也是中心对称图形,故此选项符合题意;
D、是轴对称图形,不是中心对称图形,故此选项不合题意;
故选:C.
【点睛】此题主要考查了轴对称图形和中心对称图形定义,关键是掌握如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.如果一个图形绕某一点旋转180°后能够与自身重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.
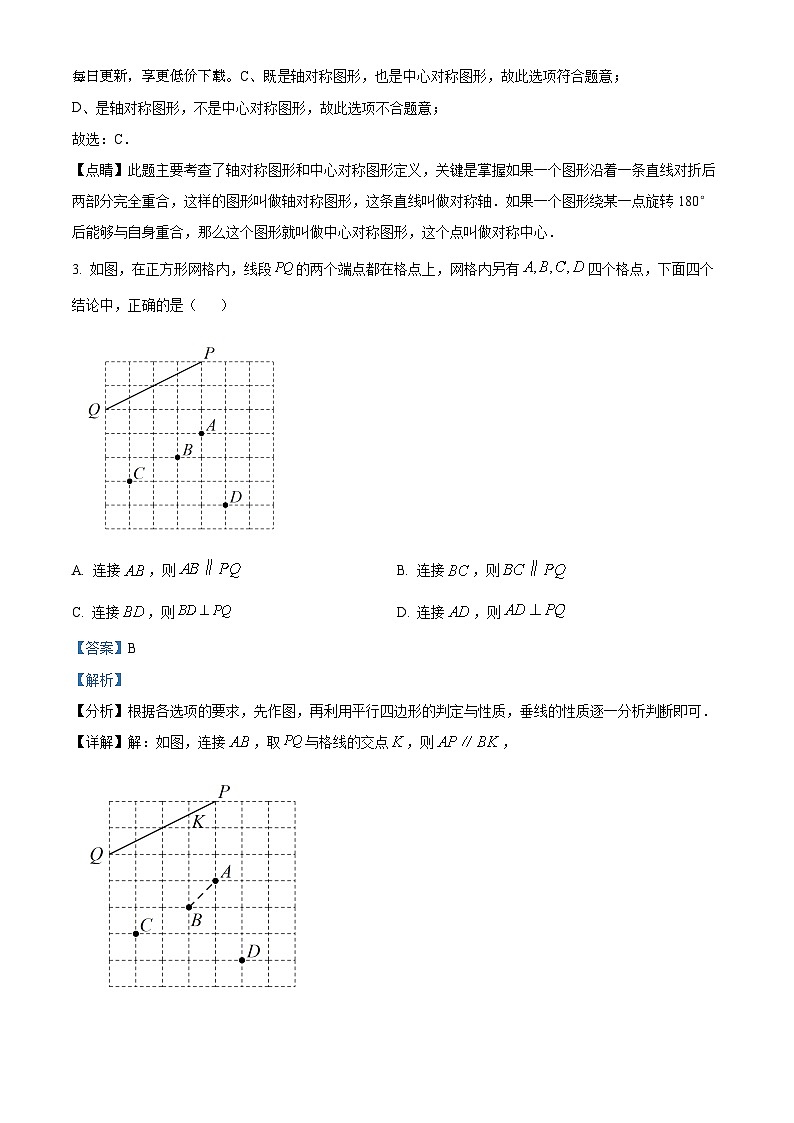
3. 如图,在正方形网格内,线段的两个端点都在格点上,网格内另有四个格点,下面四个结论中,正确的是( )
A. 连接,则B. 连接,则
C. 连接,则D. 连接,则
【答案】B
【解析】
【分析】根据各选项的要求,先作图,再利用平行四边形的判定与性质,垂线的性质逐一分析判断即可.
【详解】解:如图,连接,取与格线的交点,则,
而,
∴四边形不是平行四边形,
∴,不平行,故A不符合题意;
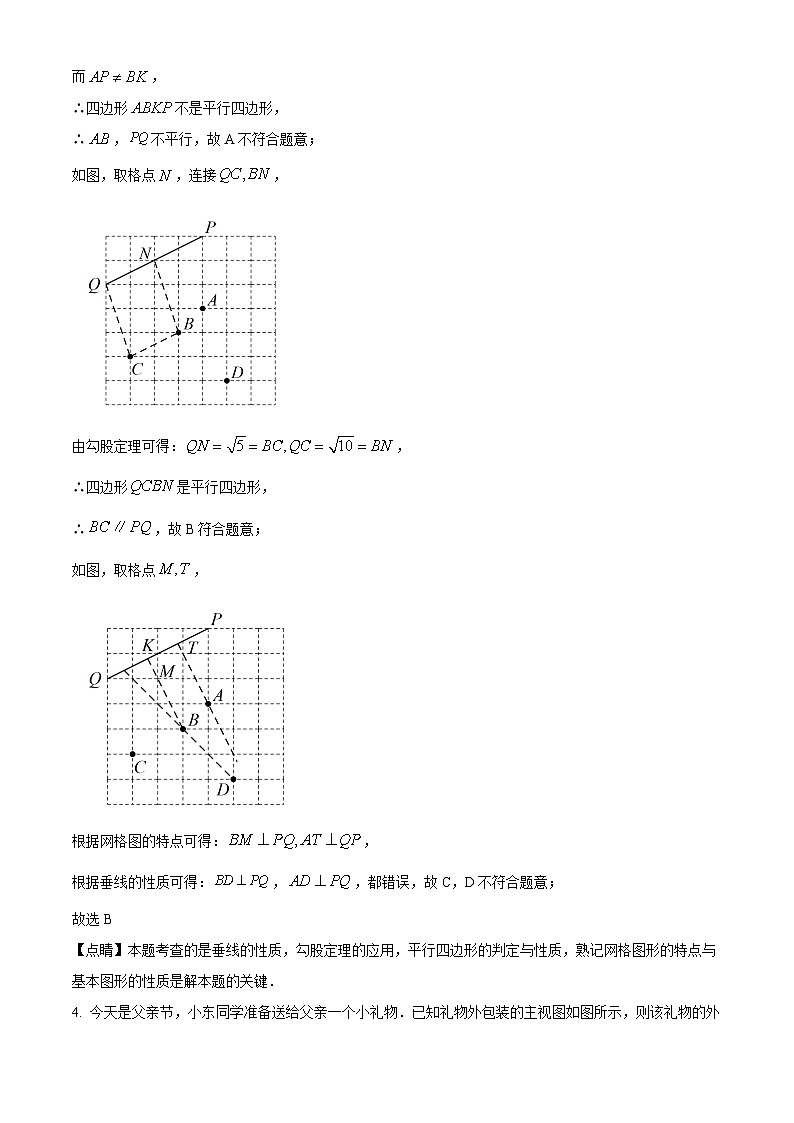
如图,取格点,连接,
由勾股定理可得:,
∴四边形是平行四边形,
∴,故B符合题意;
如图,取格点,
根据网格图的特点可得:,
根据垂线的性质可得:,,都错误,故C,D不符合题意;
故选B
【点睛】本题考查的是垂线的性质,勾股定理的应用,平行四边形的判定与性质,熟记网格图形的特点与基本图形的性质是解本题的关键.
4. 今天是父亲节,小东同学准备送给父亲一个小礼物.已知礼物外包装的主视图如图所示,则该礼物的外包装不可能是( )
A. 长方体B. 正方体C. 圆柱D. 三棱锥
【答案】D
【解析】
【分析】由长方体,正方体,圆柱的主视图是长方形,而三棱锥的主视图是三角形,从而可得答案.
【详解】解:∵长方体,正方体,圆柱的主视图是长方形,而三棱锥的主视图是三角形,
∴该礼物的外包装不可能是三棱锥,
∴A,B,C不符合题意,D符合题意;
故选D
【点睛】本题考查的是简单几何体的主视图,熟记简单几何体的三种视图是解本题的关键.
5. 下列运算正确的是( )
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了同底数幂的除法:、为正整数,.也考查了同底数幂的乘法、幂的乘方与积的乘方以及合并同类项.分别根据同底数幂相乘,底数不变指数相加;幂的乘方,底数不变指数相乘;同底数幂相除,底数不变指数相减,合并同类项,只把系数相加减,字母与字母的次数不变,对各选项计算后利用排除法求解.
【详解】解:A、与不同类项,无法合并,所以A选项不正确;
B、,所以B选项正确;
C、,所以C选项不正确;
D、,所以D选项不正确.
故选:B.
6. 不等式组的解集在数轴上表示为( )
A. B.
C. D.
【答案】D
【解析】
【分析】本题考查了解一元一次不等式组,在数轴上表示不等式组的解集,先求出不等式组的解集,再把解集在数轴上表示出来即可求解,正确求出不等式组的解集是解题的关键.
【详解】解:,
解不等式得,,
解不等式得,,
∴不等式组的解集为,
∴不等式组的解集在数轴上表示为:
故选:.
7. 实数a,b,c在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
【答案】B
【解析】
【分析】根据a,b,c对应的点在数轴上的位置,逐一判断即可.
【详解】解:由题意得:−3<a<−2<−1<b<0<3<c<4
∴a<b<c,|b|<|c|,a+c>0,ab
故选B.
【点睛】本题考查的是有理数的大小比较,绝对值的概念,有理数的和的符号,积的符号的确定,掌握以上知识是解题的关键.
8. 如图,平面直角坐标系中有M,N、P,Q四个点,其中的三个点在同一反比例函数的图象上,则不在这个图象上的点是( )
A. 点NB. 点MC. 点PD. 点Q
【答案】A
【解析】
【分析】分别设出点M、N、P、Q四点所在的反比例函数的解析式,分别求出各点对应的k值,找出与其他三个不同的k值即可.
【详解】解:设点M、N、P、Q四点所在的反比例函数分别为、、、,
∴、、、分别代入反比例函数,可得:
、、、,
从上面的求值情况可明显看出:点M、P、Q在反比例函数的图象上,点N不在这个反比例函数图象上,
故选:A.
【点睛】本题考查反比例函数图象上点的坐标特征,熟练掌握所在反比例函数上的点的横坐标与纵坐标的积等于比例系数是解题的关键.
9. 几名同学租一辆面包车去旅游,面包车的租价为240元,出发时又增加了2名同学,结果每个同学比原来少分摊了4元钱车费,设实际参加旅游的同学共x人,则所列方程为( )
A. B.
C. D.
【答案】B
【解析】
【分析】设参加旅游的同学共x人,原有人数为(x-2)人,根据每个同学比原来少分摊了4元钱车费,列方程.
【详解】解:设参加旅游的同学共x人,原有人数为(x-2)人,
由题意得,
故选B.
【点睛】本题考查由实际问题抽象出分式方程,解题关键是读懂题意,设出未知数,找出合适的等量关系,列方程即可.
10. 如图,在平面直角坐标系中,点的坐标为,点的坐标为,以为边作矩形.动点分别从点同时出发,以每秒1个单位长度的速度沿向终点移动.当移动时间为4秒时,的值为( )
A. B. C. D.
【答案】D
【解析】
【分析】根据题意,得出,,勾股定理求得,,即可求解.
【详解】解:连接、
∵点的坐标为,点的坐标为,以为边作矩形.
∴,
则,
依题意,,
∴,则,
∴
∴,
∴,
∵,
∴
故选:D.
【点睛】本题考查了坐标与图形,勾股定理求两点坐标距离,矩形的性质,求得的坐标是解题的关键.
11. 如图,直线,直线分别交,于点,,以点为圆心,长为半径画弧,若在弧上存在点使,则的度数是( )
A. B. C. D.
【答案】A
【解析】
【分析】先利用作法得到,利用等腰三角形的性质得到,于是可以计算出,再根据平行线的性质得到,然后根据邻补角的定义得到的度数.
【详解】解:如图所示,
,
由作法得:,
,
,
,
,
,
,
故选:A.
【点睛】本题考查了作图—复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作,也考查了平行线的性质,等腰三角形的性质.
12. 一种燕尾夹如图1所示,图2是在闭合状态时的示意图,图3是在打开状态时的示意图(此时),相关数据如图(单位:cm).从图2闭合状态到图3打开状态,点B,D之间的距离减少了( )
A. 2cmB. 3cmC. 4cmD. 5cm
【答案】B
【解析】
【分析】根据相似三角形的判定和性质定理即可得到结论.
【详解】解:连接,如图所示:
由题意得,,,
∴,
,
,
,
点,之间的距离减少了,
故选:B.
【点睛】本题考查了相似三角形的应用,正确的识别图形是解题的关键.
13. 中国古代数学家赵爽设计的“弦图”蕴含了丰富的数学知识.如图,在由四个全等的直角三角形(,,,)和中间一个小正方形拼成的大正方形中,设,若,则正方形与正方形的面积的比值为( )
A. B. C. D.
【答案】A
【解析】
【分析】本题考查了勾股定理和锐角三角函数的知识,设小直角三角形的长直角边为,短直角边为,斜边长为,分别表示出和,根据,可得,即可求出,,进而求解,根据和的关系得到小直角三角形两直角边的关系是解题的关键.
【详解】解:设小直角三角形的长直角边为,短直角边为,斜边长为,
∵四边形是正方形,
∴,
∴,
∴,,
∵,
∴,
∴,
∵,
,
∴正方形与正方形的面积的比值为,
故选:.
14. 如图,要围一个矩形菜园,其中一边是墙,且的长不能超过,其余的三边,,用篱笆,且这三边的和为,有下列结论:
①的长可以为;
②的长有两个不同的值满足菜园面积为;
③菜园面积的最大值为.
其中正确的是( )
A. ①②B. ①③C. ②③D. ①②③
【答案】C
【解析】
【分析】本题考查一元二次方程和二次函数的应用,理解题意,找出等量关系列出函数解析式和方程是解题的关键.设的边长为,则边的边长为,根据列出方程,再求解根据x的取值范围判断即可①;根据矩形的面积为192,列方程求解即可判断②;设矩形的菜园面积为,根据矩形的面积公式列方程,再根据二次函数的性质求函数最值即可判断③.
【详解】解:设的边长为,则边的边长为,
当时,,
解得,
∵的长不能超过,
∴,故①错误;
∵当菜园面积为时,,
整理得,,
解得或,
∴的长有两个不同的值满足菜园面积为,故②正确;
设矩形的菜园面积为,
根据题意得,,
∵,,
∴当时,y有最大值,最大值为200,故③正确;
故选:C.
15. 如图,是半圆的直径,点在半圆上,,连接,过点作,交的延长线于点.设的面积为的面积为,若,则的值为( )
A. B. C. D.
【答案】A
【解析】
【分析】如图,过作于,证明,由,即,可得,证明,可得,设,则,可得,,再利用正切的定义可得答案.
【详解】解:如图,过作于,
∵,
∴,
∵,即,
∴,
∵,
∴,
∴,即,
设,则,
∴,
∴,
∴,
∵,
∴,
∴;
故选A
【点睛】本题考查的是圆周角定理的应用,勾股定理的应用,锐角三角函数的应用,作出合适的辅助线构建直角三角形是解本题的关键.
16. 对于二次函数,定义函数是它的相关函数.若一次函数与二次函数的相关函数的图象恰好两个公共点,则的值可能是( )
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了一次函数与二次函数的交点问题,二次函数的图象和性质,分两种情况解答:一次函数分别与,相交一点;一次函数与有两个交点,与不相交 ;求出的取值范围,即可求解,掌握二次函数的图象和性质是解题的关键.
【详解】解:当时,二次函数的相关函数为
当时,二次函数的相关函数为,
∴二次函数的相关函数为,
二次函数的图象开口向上,与轴的交点为,对称轴为直线,
当时,随的增大而减小,当 时,随的增大而增大;
二次函数的图象开口向下,与轴的交点为,对称轴为直线,当时,随的增大而增大;
一次函数与轴的交点为
一次函数与二次函数的相关函数的图象恰好两个公共点可分为两种情况:
一次函数分别与,相交一点,
则有,
解得;
一次函数与有两个交点,与不相交 ,
则有,
解得,
且,
即有两个不相等的实数根,
∴,
解得,
∴;
综上所述,或,
∴值可能是,
故选:.
二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,19题每空2分)
17. 关于的一元二次方程有两个相等的实数根,则的值为 _____.
【答案】
【解析】
【分析】根据判别式的意义得到,然后解一次方程即可.
【详解】解:根据题意得,
解得.
故答案为:.
【点睛】本题考查了一元二次方程的判别式,熟练掌握一元二次方程的判别式的意义是解题的关键.
18. 如图,在平面直角坐标系中,点B在函数的图象上,点A在函数图象上,若,,则k的值为______.
【答案】
【解析】
【分析】本题考查了反比例函数的几何意义,相似三角形的性质与判定,分别过引轴的垂线,垂足分别为,证明,根据相似三角形的性质可得,进而求得,根据反比例函数的几何意义即可求得的值.
【详解】解:如图,分别过A、B引轴的垂线,垂足分别为,
点B在函数的图象上,
,
,
,
轴,轴,
,,
,
,
又,
,
,
点A在函数的图象上,
,
∵(函数图象经过第二象限),
∴,
故答案为:.
19. 如图,矩形中,是边上的动点,连接点与边的中点,将沿翻折得到,延长交边于点,作的平分线,交边于点.
(1)若,则______°;
(2)若,且三点共线,则______.
【答案】 ①. ②.
【解析】
【分析】(1)由直角三角形的性质及折叠性质得的度数,再由矩形的性质及角平分线的条件即可求解;
(2)由面积相等可求得,从而得,由勾股定理得,则可表示,在中由勾股定理建立方程即可求得.
【详解】解:(1)矩形中,,
∴,;
由折叠知:,
∴,;
∵平分,
∴;
故答案为:55;
(2)∵,
∴,
∵,
∴,
∴;
∵,
∴;
由折叠知,,;
∵E为中点,
∴,
∴;
由勾股定理得,
∴,
在中,由勾股定理得:,
即,
解得:;
故答案为:.
【点睛】本题考查了矩形的性质与折叠问题,勾股定理,等腰三角形的判定,角平分线的定义等知识,灵活运用这些知识是关键.
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
20. 解方程组,下面是两同学的解答过程:
甲同学:
解:把方程变形为,再将代入方程①得,…
乙同学:
解:将方程的两边乘以3得,再将①+②,得到,…
(1)甲同学运用的方法是________,乙同学运用的方法是________;(填序号)
①代入消元法;②加减消元法.
(2)请选择一种解法,写出完整的解答过程.
【答案】(1)①;② (2)
【解析】
【分析】本题考查了代入消元法和加减消元法解二元一次方程组.
(1)得到等式的性质进行消元,消元的目的就是将二元一次方程转化为一元一次方程;
(2)用代入消元法或加减消元法解二元一次方程组即可.
【小问1详解】
解:甲同学运用的方法是①,乙同学运用的方法是②;(填序号)
①代入消元法;②加减消元法
故答案为:①,②;
【小问2详解】
解:选择甲同学的方法,
把方程变形为,
再将代入方程①得,
解得,
把代入,得,
∴方程组的解为;
选择乙同学的方法,
将方程的两边乘以3得③,
再将①+③,得到,
解得,
把代入,得,
解得,
∴方程组的解为.
21. 一只不透明的袋子中装有4个小球,分别标有编号,这些小球除编号外都相同.
(1)搅匀后从中任意摸出1个球,这个球的编号是2的概率为________________.
(2)搅匀后从中任意摸出1个球,记录球的编号后放回、搅匀,再从中任意摸出1个球.求第2次摸到的小球编号比第1次摸到的小球编号大1的概率是多少?(用画树状图或列表的方法说明)
【答案】(1)
(2)
【解析】
【分析】(1)直接利用概率公式求解即可求得答案;
(2)画树状图表示所有等可能出现的情况,从中找出符合条件的结果数,进而求出概率.
【小问1详解】
解:搅匀后从中任意摸出1个球,这个球的编号是2的概率为;
【小问2详解】
如图,画树状图如下:
所有可能的结果数为16个,第2次摸到的小球编号比第1次摸到的小球编号大1的结果数为3个,
∴第2次摸到的小球编号比第1次摸到的小球编号大1的概率为:.
【点睛】本题考查简单随机事件的概率计算,利用列表法或树状图法求等可能事件发生的概率,使用此方法一定注意每一种结果出现的可能性是均等的,即为等可能事件.
22. (1)若关于的多项式中不含有项,则的值为______.
(2)完全平方公式经过适当的变形,可以解决很多数学问题.
例如:若,求的值.
解:∵,
根据上面的解题思路与方法解决下列问题:
i)如图,点是线段上的一点,分别以为边向直线两侧作正方形,正方形.设,两正方形的面积和为40,则的面积为______;
ii)若,求的值.
【答案】(1)6;(2)(i)6(ii)5
【解析】
【分析】本题考查完全平方公式的几何背景:
(1)将原多项式去括号、合并同类项,令项的系数为0,求出m的值即可;
(2)(i)分别设正方形和的边长分别为未知数,得到二者之和、二者平方之和,从而得到二者之积,进而可求得的面积;(ii)分别用字母表示和,从而得到二者之和、二者之积,计算二者平方之和即可.
【详解】解:(1)
,
∵不含有项,
∴,
∴,
故答案为:6.
(2)(i)设正方形和的边长分别为a和b,则的面积为;
根据题意,得,
∵,
∴,
∴,
故答案为:6.
(ii)令,,则,
∴
∵,
∴,
∴,
∴,
∴.
23. 四边形不具有稳定性,工程上可利用这一性质解决问题.如图是某篮球架的侧面示意图,为长度固定的支架,支架在处与立柱连接(垂直于,垂足为),在处与篮板连接(所在直线垂直于),是可以调节长度的伸缩臂(旋转点处的螺栓改变的长度,使得支架绕点旋转,从而改变四边形的形状,以此调节篮板的高度).已知,测得时,点离地面的高度为.调节伸缩臂,将由调节为,判断点离地面的高度升高还是降低了?升高(或降低)了多少?(参考数据:)
【答案】点离地面的高度升高了,升高了.
【解析】
【分析】如图,延长与底面交于点,过作于,则四边形为矩形,可得,证明四边形是平行四边形,可得,当时,则,此时,,,当时,则,,从而可得答案.
【详解】解:如图,延长与底面交于点,过作于,则四边形为矩形,
∴,
∵,,
∴四边形是平行四边形,
∴,
当时,则,
此时,,
∴,
当时,则,
∴,
而,,
∴点离地面的高度升高了,升高了.
【点睛】本题考查的是平行四边形的判定与性质,矩形的判定与性质,解直角三角形的实际应用,理解题意,作出合适的辅助线是解本题的关键.
24. 在直角坐标系中,设函数(是常数,).
(1)若该函数的图象经过和两点,求函数的表达式;
(2)已知,当(是实数,)时,该函数对应的函数值分别为若,求证:.
【答案】(1)
(2)见解析
【解析】
【分析】本题考查了待定系数法求二次函数表达式,代数式的化简,并利用配方法判断代数式的取值范围,第(2)小问的关键是利用,首先对代数式化简,然后配方说明的范围.
(1)使用待定系数法求二次函数解析式,将两点坐标代入,解二元一次方程组即可.
(2)已知,则,容易得到,利用,即代入,对代数式进行化简,并配方得出,最后注意利用条件判断,得证.
【小问1详解】
由题意,得
解得,
所以,该函数表达式为.
【小问2详解】
由题意,得,,
所以
,
由条件,知,
所以.
25. 在矩形中,已知,连接,,点O是边上的一动点,的半径为定值r.
(1)如下图,当经过点C时,恰好与相切,求的半径r;
(2)如下图,点M是上的一动点,求三角形面积的最大值:
(3)若从B出发,沿BC方向以每秒一个单位长度向C点运动,同时,动点E,F分别从点A,点C出发,其中点E沿着AD方向向点D运动,速度为每秒1个单位长度,点F沿着射线方向运动,速度为每秒2个单位长度,连接,如下图所示,当平移至点C(圆心O与点C重合)时停止运动,点E,F也随之停止运动.设运动时间为t(秒).在运动过程中,是否存在某一时间t,使与相切,若存在,请求出此时t的值;若不存在,请说明理由.
【答案】(1)
(2)
(3) 或
【解析】
【分析】(1)连接,,根据矩形的性质及得,进而可得,再利用解直角三角形即可求解.
(2)过点作并延长,交于,交于,当点运动到点位置时,此时三角形面积有最大值,利用矩形的性质及三角形的面积公式即可求解.
(3)分类讨论:①在的左侧时,②在的右侧侧时,利用相似三角形的判定及性质和勾股定理即可求解.
【小问1详解】
解:连接,,如图:
四边形是矩形,
,
在中,,,
,,
与对角线相切于点,
,
在和中,
,
,
,
,
的半径.
【小问2详解】
过点作并延长,交于,交于,如图:
由(1)得:,,
,
四边形是矩形,且,
,
当点运动到点位置时,此时三角形面积有最大值,
.
【小问3详解】
在整个运动过程中,存在某一时刻,与相切,此时值为或,理由:
由(1)得,
①在的左侧时,设与相切于点,
连接,,如图:
由题意得:,,
,
四边形为矩形,
,,
,
四边形为矩形,
,,
与相切于点,
,
,
,
,
,
,
,
,
,
或(不合题意舍去),
②在的右侧侧时,
设与相切于点,连接,,如图:
由题意得: , ,
,
四边形为矩形,
,,
,
四边形为矩形,
,,
与相切于点,
,
,
,
,
,
,
,
,
,
或(不合题意舍去),
综上所述,t的值为 或.
【点睛】本题考查了相似三角形的判定及性质、矩形的性质、解直角三角形、切线的性质、勾股定理,熟练掌握相关判定及性质,利用分类讨论思想解决问题是解题的关键.
26. 某动力科学研究院实验基地内装有一段笔直的轨道,长度为的金属滑块在上面做往返滑动.如图,滑块首先沿方向从左向右匀速滑动,滑动速度为,滑动开始前滑块左端与点重合,当滑块右端到达点时,滑块停顿,然后再以小于的速度匀速返回,直到滑块的左端与点重合,滑动停止.设时间为时,滑块左端离点的距离为,右端离点的距离为,记与具有函数关系.已知滑块在从左向右滑动过程中,当和时,与之对应的的两个值互为相反数;滑块从点出发到最后返回点,整个过程总用时(含停顿时间).请你根据所给条件解决下列问题:
(1)滑块从点到点的滑动过程中,的值________________;(填“由负到正”或“由正到负”)
(2)滑块从点到点滑动过程中,求与的函数表达式;
(3)在整个往返过程中,若,求的值.
【答案】(1)由负到正
(2)
(3)当或时,
【解析】
【分析】(1)根据等式,结合题意,即可求解;
(2)设轨道的长为,根据已知条件得出,则,根据当和时,与之对应的的两个值互为相反数;则时,,得出,继而求得滑块返回的速度为,得出,代入,即可求解;
(3)当时,有两种情况,由(2)可得,①当时,②当时,分别令,进而即可求解.
【小问1详解】
∵,
当滑块在点时,,,
当滑块在点时,,,
∴的值由负到正.
故答案为:由负到正.
【小问2详解】
解:设轨道的长为,当滑块从左向右滑动时,
∵,
∴,
∴
∴是的一次函数,
∵当和时,与之对应的的两个值互为相反数;
∴当时,,
∴,
∴,
∴滑块从点到点所用的时间为,
∵整个过程总用时(含停顿时间).当滑块右端到达点时,滑块停顿,
∴滑块从点到点的滑动时间为,
∴滑块返回的速度为,
∴当时,,
∴,
∴,
∴与的函数表达式为;
【小问3详解】
当时,有两种情况,
由(2)可得,
①当时,,
解得:;
②当时,,
解得:,
综上所述,当或时,.
【点睛】本题考查了一次函数的应用,分析得出,并求得往返过程中的解析式是解题的关键.
2024年河北省邯郸市经开区九年级下学期中考一模数学试卷: 这是一份2024年河北省邯郸市经开区九年级下学期中考一模数学试卷,共10页。
2024年河北省邯郸市经开区中考一模数学试题(无答案): 这是一份2024年河北省邯郸市经开区中考一模数学试题(无答案),共7页。试卷主要包含了不等式的解集在数轴上表示为等内容,欢迎下载使用。
2024年河北省邯郸市经开区中考一模数学试题(原卷版+解析版): 这是一份2024年河北省邯郸市经开区中考一模数学试题(原卷版+解析版),文件包含2024年河北省邯郸市经开区中考一模数学试题原卷版docx、2024年河北省邯郸市经开区中考一模数学试题解析版docx等2份试卷配套教学资源,其中试卷共41页, 欢迎下载使用。












